УЧЕБА / Пересечение поверхностей

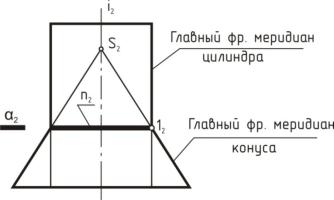
4 Способ вспомогательных секущих сфер

Как уже отмечалось выше, в качестве вспомогательных секущих поверхностей могут использоваться сферы.

Почему именно сферы выбрали в качестве поверхностей-посредников? Чтобы ответить на этот вопрос рассмотрим частный случай пересечения поверхностей вращения - пересечение соосных поверхностей.

4.1 Соосные поверхности и построение линии пересечения соосных поверхностей

Соосными называются две поверхности вращения, имеющие общую ось вращения.

Например, соосными являются цилиндр и конус на рисунке 11.

Рисунок 11

Теорема о пересечении соосных поверхностей:

Две соосные поверхности вращения пересекаются по окружностям, число которых равно числу точек пересечения полумеридианов поверхностей. Плоскости окружностей перпендикулярны к общей оси вращения.

На рисунке 11 цилиндр и конус пересекаются по окружности n (n2). Плоскость этой окружности α перпендикулярна общей оси вращения i и проходит через точку 1 – точку пересечения полумеридианов заданных поверхностей.

Если центр сферы лежит на оси какой-либо поверхности вращения, то сфера соосна с этой поверхностью и пересекает ее по окружности.

На рисунке 12 приведены примеры сфер соосных с разными поверхностями вращения и построены проекции окружностей, по которым сферы пересекают эти поверхности.

21

Рисунок 12

Свойство сфер пересекать соосные с ними поверхности вращения по окружностям и положено в основу способа вспомогательных секущих сфер.

4.2 Способ сфер-посредников

Как уже отмечалось выше, линия пересечения двух поверхностей представляет собой пространственную кривую. Чтобы построить эту кривую нужно построить множество точек, одновременно принадлежащих каждой из пересекающихся поверхностей. Порядок нахождения общих точек с помощью вспомогательной секущей сферы рассмотрим на примере.

Пусть пересекаются две поверхности вращения: прямой круговой конус Φ и прямой круговой цилиндр Ψ (рисунок 13). Оси вращения заданных поверхностей лежат в одной плоскости и пересекаются в точке О (і ∩ j = О).

Рисунок 13

22

Алгоритм решения задачи на определение общих точек линии пересечения поверхностей.

1.Вводим вспомогательную секущую сферу с центром в точке О. Центр сферы точка О совпадает с точкой пересечения осей вращения (і ∩ j = О). В этом случае сфера будет соосна с каждой из заданных поверхностей.

2.Строим линию пересечения сферы с конусом. Это будет окружность m.

3.Строим линию пересечения сферы с цилиндром. Это будет окружность

n.

4.Находим точки пересечения двух окружностей – точки А и В. Это и будет первая пара искомых точек.

m ∩ n ={ A; B }

Если в той же точке О, как в центре, построить еще одну сферу и повторить пункты 2, 3 и 4, то получим другие точки искомой линии пересечения.

Условия выбора способа сфер

Вспомогательные секущие сферы можно применить только при одновременном выполнении следующих условий:

1)пересекающиеся поверхности должны быть поверхностями вращения;

2)заданные поверхности должны иметь общую плоскость симметрии, параллельную какой-либо плоскости проекций;

3)каждая из поверхностей должна содержать семейство окружностей, по которым сферы будут пересекать эти поверхности;

а) если оси заданных поверхностей пересекаются (i ∩ j = O), выбирают способ концентрических сфер

б) если оси заданных поверхностей скрещиваются, выбирают способ эксцентрических сфер

4.3 Способ концентрических сфер

Пример. Построить линию пересечения двух поверхностей (рисунок 14).

1. Анализ условия.

Пересекаются два прямых круговых конуса. Обозначим конус с осью вращения i π1 буквой Ψ, а конус с осью j π3 буквой Φ. Обе поверхности общего вида.

2. Способ решения задачи.

Для построения линии пересечения применяем способ концентрических сфер, так как выполняются все необходимые условия:

обе поверхности – поверхности вращения;

23

имеется общая плоскость симметрии α, параллельная одной из плоскостей проекций (α ║ π2);

каждая из поверхностей несет на себе семейство окружностей (на поверхности Ψ окружности і, на поверхности Φ окружности ј);

оси поверхностей пересекаются (i ∩ j = О).

Рисунок 14

24

3. Опорные точки.

Прежде всего, отмечаем плоскости, в которых лежат опорные точки кривой пересечения.

α – фронтальная плоскость уровня. Она является общей плоскостью симметрии и общей границей видимости на π2 для заданных поверхностей.

β– горизонтальная плоскость уровня (граница видимости на π1 конуса Φ

иодновременно общая граница видимости линии пересечения на π1).

Теперь находим опорные точки, лежащие в этих плоскостях.

Общая плоскость симметрии α пересекает обе поверхности по образующим, которые являются очерковыми данных конусов на π2. В пересечении этих образующих отмечаем проекции точек А2 и В2 (точка А – самая верхняя точка кривой пересечения, точка В – самая нижняя).

Так как плоскость α является еще и общей границей видимости двух поверхностей на π2, то точки А и В – это еще и точки изменения видимости кривой пересечения на π2.

Точки изменения видимости на π1 найдем с помощью плоскости β.

а) плоскость β пересекает поверхность Ψ по окружности k (r – радиус окружности k)

β ∩ Ψ = окр.k

б) плоскость β пересекает поверхность Φ по двум образующим, которые являются очерковыми конуса Φ на π1

β ∩ Φ = две образующие (а;b);

в) при пересечении окружности k и образующих а и b получаем точки С и D, которые и будут точками изменения видимости кривой пересечения на π1;

k ∩ a = C

k ∩ b = D

Для построения остальных точек применяем способ концентрических сфер (рисунок 15). За центр сфер принимаем точку О – точку пересечения осей i и j (i ∩ j = О)

Чтобы избежать лишних построений, необходимо определить размеры радиусов наименьшей и наибольшей сфер, пригодных для решения задачи.

Радиус максимальной сферы (Rmax) определяем как расстояние от точки О до наиболее удаленной точки пересечения фронтальных меридианов (очерковых образующих) заданных поверхностей.

О2А2 < О2В2 => Rmax = О2В2

Радиус минимальной сферы (Rmin) равен наибольшему из расстояний от точки О до очерковых образующих пересекающихся поверхностей.

Для нахождения Rmin из проекции точки О (О2 ) проводим два перпендикуляра к очерковым образующим поверхностей.

O2M2 > O2N2 => Rmin = O2M2

25

Таким образом, сфера минимального радиуса должна быть вписана в одну поверхность, а другую пересекать.

Нахождение первой пары точек с помощью минимальной сферы

а) вводим сферу радиусом Rmin;

б) сфера Rmin пересекает поверхность Ψ по окружности m (m2); в) сфера Rmin пересекает поверхность Φ по окружности n (n2); г) отмечаем точки пересечения полученных окружностей

m ∩ n = {1;1'}

Точки 1 и 1' будут самыми правыми точками искомой линии пересечения.

4. Промежуточные точки.

Для построения других точек линии пересечения, применяем сферы, которые будут находиться между наибольшей и наименьшей сферами.

(Rmin < Ri < Rmax).

Например, чтобы построить промежуточные точки 2 и 2' вводим вспомогательную секущую сферу радиусом R. Эта сфера пересекает поверхность Ψ по окружности с, а поверхность Φ - по окружности d. Пересечение фронтальных проекций этих окружностей дает точки 22 и 22'.

5. Видимость линии пересечения.

Общей границей видимости на π2 является плоскость α. Так как линия пересечения симметрична относительно плоскости α, то на π2 видимая часть кривой пересечения закрывает невидимую. Точки невидимые на π2 (2', D, 1') на чертеже взяты в скобки.

Общей границей видимости на π1 является плоскость β. Часть линии пересечения, расположенная ниже плоскости β, будет на π1 не видна. Поэтому, участок кривой от точки В до точек С и D на π1 изображаем штриховой линией.

6. Видимость очерков.

Очерком конуса Ψ на плоскости π1 является его основание. Очерковыми конуса Φ на π1 являются его образующие а и в. Основание находится ниже образующих а и в, следовательно на π1 оно будет не видимо ( в пределах площади наложения проекций Φ1 и Ψ1).

Проекции прямых а1 и в1 будут видимы на π1 до точек C1 и D1 (в точках С и D прямые врезаются в конус Ψ и растворяются в нем).

27

4.4 Способ эксцентрических сфер

Пример. Построить линию пересечения поверхностей.

1. Анализ условия.

Пересекаются две поверхности: прямой круговой конус Φ и открытый тор Ψ. Обе поверхности общего положения (рисунок 17).

2. Способ решения задачи.

Для построения линии пересечения поверхностей выбираем способ эксцентрических сфер, так как выполняются все необходимые условия:

обе пересекающиеся поверхности – поверхности вращения;

имеется общая плоскость симметрии α, параллельная фронтальной плоскости проекций (α║π2);

каждая из поверхностей несет на себе семейство окружностей;

оси заданных поверхностей скрещиваются.

Более подробно рассмотрим третье условие, т. е. ответим на вопрос «какие семейства окружностей несут на себе тор и конус».

На поверхности конуса окружности (параллели) расположены перпендикулярно оси ј. На поверхности тора можно выделить два семейства окружностей (рисунок 16):

а) параллели, получающиеся при пересечении тора плоскостями перпендикулярными оси i

(α і);

б) меридианы, получающиеся при пересечении тора плоскостями, проходящими через ось i

(σ ј).

Рисунок 16

28

3. Опорные точки.

Прежде всего, отмечаем плоскости, в которых лежат опорные точки линии пересечения (рисунок 17).

α – фронтальная плоскость уровня. Она является общей плоскостью симметрии заданных поверхностей и одновременно общей границей видимости на

π2.

β – горизонтальная плоскость уровня. Она является границей видимости конуса на π1 и одновременно общей границей видимости на

π1.

Рисунок 17

Для нахождения опорных точек, лежащих в плоскости α, пересечем заданные поверхности этой плоскостью.

а) плоскость α пересекает конус по двум образующим f и f ', которые являются очерковыми конуса на π2;

α ∩ Φ = { f, f '}

б) плоскость α пересекает тор по двум параллелям - экватору и горлу, которые являются очерковыми тора на π2;

α ∩ Ψ = {экватор, горло} в) при пересечении фронтальных проекций полученных линий отмечаем

проекции опорных точек А и В.

f ∩ экватор = А (А – самая верхняя точка линии пересечения) f ' ∩ горло = В (В – самая нижняя точка линии пересечения)

29

Плоскость β пересекает конус по двум образующим, тор – по кривой четвертого порядка, строить которую сложно. Поэтому точки изменения видимости на π1 определяют приблизительно после построения фронтальной проекции линии пересечения.

4. Промежуточные точки.

Прежде всего, через ось тора ј (ј2) проводим вспомогательную секущую плоскость δ (δ2) (рисунок 18). Эта плоскость пересекает тор по окружности

d(d2).

δ ∩ Ψ = окр.d

Отмечаем центр этой окружности – точку О (О2).

Центр сферы, пересекающей тор по окружности d, будет расположен на прямой n, проходящей через точку О и перпендикулярной к плоскости этой окружности (n δ).

Чтобы вспомогательная сфера пересекала и конус по окружности, центр сферы должен лежать на оси конуса.

Из вышесказанного следует, что центр вспомогательной сферы находится как точка пересечения прямой n с осью i.

n ∩ i = P – центр первой вспомогательной сферы.

Затем, используя общий алгоритм, находим первую пару промежуточных точек. Для этого:

1)проводим вспомогательную секущую сферу с центром в точке P и радиусом R;

2)вспомогательная сфера пересекает конус по окружности m (m2);

3)вспомогательная сфера пересекает тор по окружности d (d2);

4)находим точки пересечения окружности m и d (это и будет первая пара искомых точек).

m ∩ d = {1;1'}

Аналогично находим следующую пару промежуточных точек 2 и 2'. Проводим вспомогательную секущую плоскость δ'. Эта плоскость пересекает тор по окружности. Отмечаем центр окружности – точку О' (О'2). Проводим прямую n' δ'. Находим точку пересечения прямой n' с осью i (n'2 ∩ i2 = P'2). Точка P'2 и будет центром второй вспомогательной сферы. Затем повторяем общий алгоритм с первого по четвертый пункты.

5. Видимость линии пересечения.

Общей границей видимости на π2 является плоскость α – общая плоскость симметрии. Линия пересечения симметрична относительно этой плоскости. Следовательно, видимая часть линии пересечения полностью закрывает невидимую. Точки невидимые на π2 (1', D, 2') на чертеже взяты в скобки.

30