ТИПОВОЙ РАСЧЁТ ПО ТЕМЕ: «РЯДЫ»
Вариант № 1
№ 1. Выписать
члены
:
№ 2. Записать ряды с использованием знака бесконечной суммы:
№ 3. Найти сумму
ряда:
.
№ 4. Исследовать ряды, применяя необходимый признак сходимости:
.
№ 5. Исследовать ряды на сходимость, применяя признак Даламбера:
.
№ 6. Исследовать ряды на сходимость, применяя признак Коши:
.
№ 7. Исследовать ряды, применяя интегральный признак сходимости:
.
№ 8. Исследовать сходимость рядов:
.
№ 9. Исследовать сходимость рядов, применяя один из признаков сравнения:
.
№ 10. Исследовать ряды на сходимость:
.
№ 11. Найти интервал сходимости и исследовать поведение ряда на концах интервала:
.
№ 12. Написать три первые члена разложения функций в ряд Тейлора:
№ 13. Разложить
функцию
в ряд Маклорена, почленно проинтегрировав
разложение в ряд по степенямx
производной
этой функции.
Исследовать полученный ряд на сходимость.
№ 14. Разложить
функцию
в ряд Маклорена, используя приведенное
равенство и теорему о почленном
интегрировании суммы ряда.
№ 15. Разложить функции в ряд Тейлора, используя стандартные разложения:
.
№ 16. Функцию
разложить в ряд Фурье в интервале [0;
2].
№ 17. Периодическую
функцию
,
определенную на [0;
1], разложить в
ряд Фурье дважды: доопределив её на
интервале [-1;
0] :
а) четным;
б) нечетным образом.
ТИПОВОЙ РАСЧЁТ ПО ТЕМЕ: «РЯДЫ»
Вариант № 2
№ 1. Выписать
члены
:
№ 2. Записать ряды с использованием знака бесконечной суммы:
№ 3. Найти сумму
ряда:
.
№ 4. Исследовать ряды, применяя необходимый признак сходимости:
.
№ 5. Исследовать ряды на сходимость, применяя признак Даламбера:
.
№ 6. Исследовать ряды на сходимость, применяя признак Коши:
.
№ 7. Исследовать ряды, применяя интегральный признак сходимости:
.
№ 8. Исследовать сходимость рядов:
.
№ 9. Исследовать сходимость рядов, применяя один из признаков сравнения:
.
№ 10. Исследовать
ряды на сходимость:
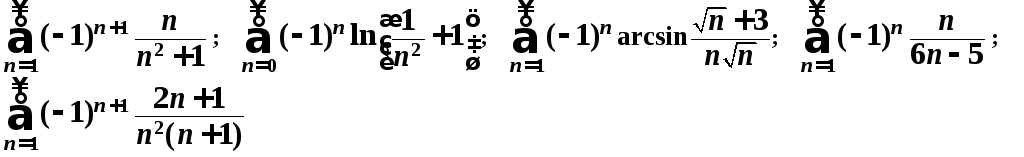
№ 11. Найти интервал сходимости и исследовать поведение ряда на концах интервала:
.
№ 12. Написать три первые члена разложения функций в ряд Тейлора:
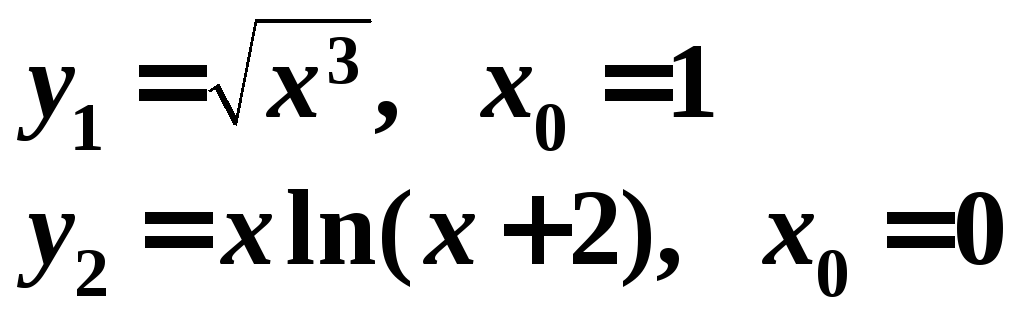
№ 13. Разложить
функцию
в ряд Маклорена, почленно проинтегрировав
разложениев
ряд по степеням
x
производной
этой
функции.
Исследовать
полученный ряд на сходимость.
№ 14. Разложить
функцию
в ряд Маклорена, используя приведенное
равенство и теорему о почленном
интегрировании суммы ряда.
№ 15. Разложить функции в ряд Тейлора, используя стандартные разложения:
.
№ 16. Функцию
разложить в ряд Фурье в интервале [0;
2].
№ 17. Периодическую
функцию
,
определенную на [0;
1], разложить в
ряд Фурье дважды: доопределив её на
интервале [-1;
0] :
а) четным;
б) нечетным образом.
ТИПОВОЙ РАСЧЁТ ПО ТЕМЕ: «РЯДЫ»
Вариант № 3
№ 1. Выписать
члены
:
№ 2. Записать ряды с использованием знака бесконечной суммы:
№ 3. Найти сумму
ряда:
.
№ 4. Исследовать ряды, применяя необходимый признак сходимости:
.
№ 5. Исследовать ряды на сходимость, применяя признак Даламбера:
.
№ 6. Исследовать ряды на сходимость, применяя признак Коши:
.
№ 7. Исследовать ряды, применяя интегральный признак сходимости:
.
№ 8. Исследовать сходимость рядов:
.
№ 9. Исследовать сходимость рядов, применяя один из признаков сравнения:
.
№ 10. Исследовать
ряды на сходимость:
№ 11. Найти интервал сходимости и исследовать поведение ряда на концах интервала:
.
№ 12. Написать три первые члена разложения функций в ряд Тейлора:
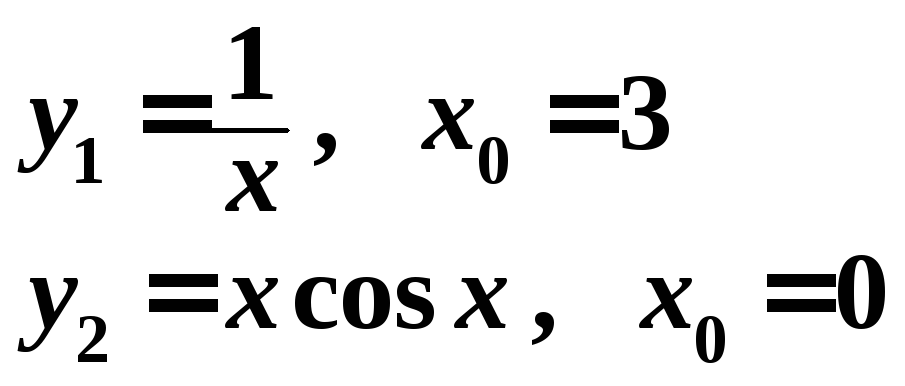
№ 13. Разложить
функцию
в ряд Маклорена, почленно проинтегрировав
разложениев
ряд по степеням
x
производной
этой
функции.
Исследовать
полученный ряд на сходимость.
№ 14. Разложить
функцию
в ряд Маклорена, используя приведенное
равенство и теорему о почленном
интегрировании суммы ряда.
№ 15. Разложить функции в ряд Тейлора, используя стандартные разложения:
.
№ 16. Функцию
разложить в ряд Фурье в интервале [0;
2].
№ 17. Периодическую
функцию
,
определенную на [0;
1], разложить в
ряд Фурье дважды: доопределив её на
интервале [-1;
0] :
а) четным;
б) нечетным образом.
ТИПОВОЙ РАСЧЁТ ПО ТЕМЕ: «РЯДЫ»