
Cramer C.J. Essentials of Computational Chemistry Theories and Models
.pdf
Appendix B
Symmetry and Group Theory
B.1 Symmetry Elements
To say that something is symmetric, or that it possesses symmetry, usually is to say that an internal motif is repeated in some fashion. In the context of chemistry, that motif is a spatial arrangement of atoms. We may classify the nature of an object’s symmetry based on the fashion in which its repeated motifs are made manifest. In describing the symmetric positioning of atoms in a molecule, there are only a few different operations that are relevant for chemical systems, and these operations are referred to as ‘symmetry elements’. When a particular symmetry element is present, the molecule is said to ‘possess’ that symmetry element. The four symmetry elements that may be used to characterize a molecular structure are:
Plane of symmetry. If a plane can be placed in space such that for every atom of the molecule not in the plane there is an identical atom (which is to say, the same atomic number and isotope) on the other side of the plane at equal distance from it (i.e., a ‘mirror image’), the molecule is said to possess a plane of symmetry. The Greek letter σ is often used to represent both the plane of symmetry and the ‘operation’ of mirror reflection that it performs. An example of a molecule possessing a plane of symmetry is methylcyclobutane, as illustrated in Figure B.1. Note that a planar molecule always has at least one σ , since the plane of the molecule satisfies the above symmetry criterion in a trivial way (the set of reflected atoms is the empty set). Note also that if we choose a Cartesian coordinate system in such a way that two of the Cartesian axes lie in the symmetry plane, say x and y, then for every atom found at position (x,y,z) where z = 0 there must be an identical atom at position (x,y,−z).
Proper rotation axis. If a molecule can be rotated about some axis so that the positions originally occupied by every atom are subsequently occupied by identical atoms, the molecule is said to possess a proper rotation axis. The axis and the rotation operation performed about it are typically represented by the notation Cn, where n is the order of the rotation. The order is the largest value of n for which it is true that a rotation of 2π /n radians about the axis reproduces the original structure; this is also referred to as a n-fold rotation axis.
Essentials of Computational Chemistry, 2nd Edition Christopher J. Cramer
2004 John Wiley & Sons, Ltd ISBNs: 0-470-09181-9 (cased); 0-470-09182-7 (pbk)

558 |
|
APPENDIX B |
||
|
|
|
|
Hb′ |
|
|
Ha′ |
|
Hb |
|
H |
|
|
H |
|
|
|
Hc′ |
|
|
H |
H |
a |
Hc |
|
|
|
||
|
|
|
|
|
H |
s |
|
|
C3 |
|
S2 |
H3C |
|
|
O |
|
O |
i |
|
|
|
||
|
|
H3C |
|
|
|
|
O |
CH3 |
|
O |
|
|
|
|
|
|
|
|
|
Figure B.1 Symmetry elements possessed by various molecular conformations. The molecules illustrated here have no elements beyond those indicated, but arbitrary molecules may be characterized by many different symmetry operations
An example of a molecule with a three-fold rotation axis is the conformation of sym -1,3,5- triethylcyclohexane shown in Figure B.1. Note that all molecules possess a trivial C1 axis (indeed, an infinite number of them). Note also that if we choose a Cartesian coordinate system where the proper rotation axis is the z axis, and if the rotation axis is two-fold, then for every atom found at position (x,y,z) where x and y are not simultaneously equal to 0 (i.e., not on the z axis itself) there will be an identical atom at position (−x,−y,z). If the rotation axis is four-fold, there will be an identical atom at the three positions (−x,y,z), (x,−y,z), and (−x,−y,z). Note finally that for linear molecules the axis of the molecule is a proper symmetry axis of infinite order, i.e., C∞.
Improper rotation axis. Rotation about an improper axis is analogous to rotation about a proper symmetry axis, except that upon completion of the rotation operation, the molecule is mirror reflected through a symmetry plane perpendicular to the improper rotation axis. These axes and their associated rotation/reflection operations are usually abbreviated Sn, where n is the order of the axis as defined above for proper rotational axes. Note that an S1 axis is equivalent to a σ plane of symmetry, since the initial rotation operation simply returns every atom to its original location. Note also that the presence of an S2 axis (or indeed any S axis of even order n) implies that for every atom at a position (x,y,z) that is not the origin, there will be an identical atom at position (−x,−y,−z); the origin in such a system is called a ‘point of inversion’, since one may regard every atom as having an identical
SYMMETRY AND GROUP THEORY |
559 |
partner related by inversion through the origin, and the inversion operation itself is usually denoted i. An example of a molecule containing an S2 axis is the chair conformation of 2,5-dioxo-1,4-tetrahydropyran (Figure B.1). Lastly, note that the presence of higher order improper axes implies the simultaneous presence of one or more proper rotation axes. In particular, improper axes Sn where n is odd imply a coincident Cn axis and n perpendicular C2 axes, and improper axes Sn where n is even imply a coincident Cn/2 axis.
Point of inversion. The action of a point of inversion is described above in the context of improper rotation axes. Note that planes of symmetry and points of inversion are somewhat redundant symmetry elements, since they are already implicit in improper rotation axes. However, they are somewhat more intuitive as separate phenomena than are Sn axes, and thus most texts treat them separately.
B.2 Molecular Point Groups and Irreducible Representations
An individual molecular structure may possess no symmetry elements at all, or a single symmetry element, or some combination of multiple symmetry elements. It turns out that there are a finite number of possible combinations, and each such combination defines what is referred to as a point group. The names of the various molecular point groups together with a flow chart indicating how to assign a molecule to a point group are provided in Figure B.2. [In crystallography, solids can be characterized by space groups, which are analogous to point groups but more numerous as additional symmetry elements relating different molecules in the crystal must also be considered. No further discussion of space groups is provided here.]
There is a special algebra associated with the different point groups, and the mathematical field of group theory is devoted to this topic. Group theory is a fascinating topic, but only its most basic aspects are addressed here. To begin, all point groups other than the nonsymmetric C1 group are characterized by two or more so-called irreducible representations, or irreps for short. Operationally, an irreducible representation defines how a signed or phased fragment (e.g., an orbital) of the symmetric structure ‘transforms’ under the various possible symmetry operations that compose the point group.
For example, the Cs point group contains two irreps, usually called a and a . Fragments belonging to the a irrep are unchanged upon reflection through the symmetry plane of the molecule. Irreps leaving fragments unchanged under all symmetry operations of the point group are referred to as ‘totally symmetric’ irreps. The a irrep of the Cs point group, on the other hand, reverses the phase of a fragment on reflection through the mirror plane.
A much more detailed example is provided in Figure 6.7, where the C2v point group to which the water molecule belongs is characterized by four irreps. The totally symmetric a1 irrep includes orbitals unchanged by rotation about the C2 axis or reflection through either of the two vertical mirror planes. The a2 irrep includes orbitals that are unchanged by rotation about the C2 axis but that are inverted by reflection through either of the two vertical mirror planes (Figure 6.7 does not list any such orbitals since none exist in

560 |
|
|
|
|
|
|
|
APPENDIX B |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
yes |
|
|
|
|
|
|
yes |
|
|
|
|
|
|
||||
|
Linear |
|
|
|
|
|
Presence |
|
|
|
|
|
D∞h |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
molecule? |
|
|
|
|
|
|
|
|
|
of sh? |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
no |
||||||||||||
|
no |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
no |
|
|
|
|
|
|
C∞v |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Presence |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Presence |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
of Cn axis? |
|
|
|
|
|
|
|
|
|
|
|
|
yes |
|
|
Cs |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
of sh? |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
no |
|
||||||||
|
yes |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Multiple Cn |
|
yes |
|
|
|
|
Presence of |
|
yes |
Ci |
|||||||||||||
|
|
|
|
|
T, O, and I |
|
|
|
|
inversion |
|
|
|
|
|
|||||||||
|
axes, n ≥ 3? |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
center? |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
no |
|
||||
|
no |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
no |
|
n C2 axes |
|
|
|
|
|
|
|
|
|
C1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Presence |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
of S2n axis? |
|
|
|
|
|
|
|
|
perpendicular |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
to Cn axis? |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
no |
|
|
|
yes |
|
|
|
|
|
|
|||||||
|
yes |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yes |
|
|||
|
|
|
|
|
|
|
Presence |
|
|
|
|
|
|
Presence |
|
|
Dnh |
|||||||
|
S2n |
|
|
|
|
of sh? |
|
|
|
|
|
|
of sh? |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
no |
|
|
|
|
yes |
|
|
no |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Cnh |
|
|
|
|
|
|
yes |
|
||||
|
|
|
|
|
|
|
Presence |
|
|
|
Presence |
|
|
Dnd |
||||||||||
|
|
|
|
|
|
|
of n sv? |
|
|
|
|
|
|
of n sd? |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
no |
|
|
|
|
yes |
|
|
no |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Cn |
|
Cnv |
|
|
Dn |
|
|
|
|
|
|
||||||
Figure B.2 Flow chart for point-group assignment. A symmetry plane that is perpendicular to a proper axis of rotation is a σh plane, one that includes the unique proper axis of rotation is a σv plane, and one that includes the highest order proper axis of rotation and bisects the remaining two-fold axes of rotation is a σd plane
a minimal basis set representation, but the dxy orbital on oxygen or the antisymmetric combination of two py orbitals on the H atoms would belong to this irrep in a polarized basis set representation). The b1 irrep includes orbitals that are inverted by rotation and reflection through the σxz symmetry plane, but left unchanged by reflection through the σyz symmetry plane, and the b2 irrep includes orbitals that are inverted by rotation and reflection through the σyz symmetry plane, but left unchanged by reflection through the σxz symmetry plane.
562 |
|
|
|
APPENDIX B |
|
|
|
|
|
Table B.5 Product rules for the C2h point groupa |
|
||
|
|
|
ag |
au |
bg |
bu |
|
||||||
|
ag |
|
ag |
au |
bg |
bu |
|
au |
|
au |
ag |
bu |
bg |
|
bg |
|
bg |
bu |
ag |
au |
|
bu |
|
bu |
bg |
au |
ag |
a Objects unchanged by rotation belong to a type irreps, while objects changing phase on rotation belong to b type irreps; objects unchanged by reflection through the horizontal σ belong to −g type irreps, while objects changing phase on reflection belong to −u type irreps.
|
|
Table B.4 Product rules for the C2v point groupa |
|
||
|
|
a1 |
a2 |
b1 |
b2 |
|
|||||
a1 |
|
a1 |
a2 |
b1 |
b2 |
a2 |
|
a2 |
a1 |
b2 |
b1 |
b1 |
|
b1 |
b2 |
a1 |
a2 |
b2 |
|
b2 |
b1 |
a2 |
a1 |
a See text for irrep definitions.
orbitals, so their product must be taken to determine the state symmetry. Figure 14.4 provides examples of this process. In more complex open-shell systems, the sequential product of all of the singly occupied orbitals determines the electronic state symmetry.
Some complications can arise. Although in many point groups the product of any two irreps is another irrep (as is true for the examples in Tables B.1 through B.5), in some cases the product of two irreps can only be expressed as a linear combination of two or more different irreps. A determinant that does not belong to a single irrep is not a true wave function, but must be combined with other determinants to construct a wave function having a pure state symmetry. Such situations are beyond the scope of this text.
B.4 Symmetry in the Evaluation of Integrals and Partition
Functions
Mathematical functions and operators can be assigned to irreps just as orbitals can be. This has enormous implications for practical computations because the integral over all space of any product that does not contain the totally symmetric representation vanishes, i.e., there is no point evaluating it. The Fock and Hamiltonian operators both belong to the totally symmetric irrep of any point group, because they depend only on interparticle distances and the 2 operator, and these quantities are unaffected by changes in the coordinate system brought about by rotations, reflections, etc. Thus, in evaluating Fock matrix elements of
the form
Fµν = φµ(1)F φν (2)dr(1)dr(2) (B.1)
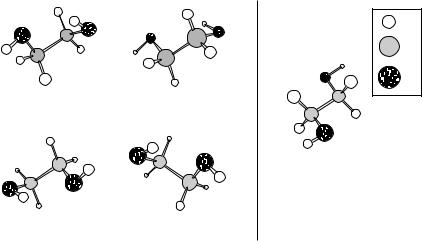
SYMMETRY AND GROUP THEORY |
563 |
H
C
O
(180,60,−60) |
(180,−60,60) |
(180,180,180)
(−60,60,180) |
(60,−60,180) |
Figure B.3 The conformer of 1,2-ethanediol shown on the left may be generated, to within enantiomeric equivalence, by four different combinations of the left-to-right dihedral angles (ωHOCC, ωOCCO, ωCCOH). The conformer on the right, on the other hand, is unique. To account for the greater phase-space volume associated with the four-fold degenerate conformer, computation of its free energy must include a term of −RT ln4
if the product of the irreps to which φµ and φν belong does not contain the totally symmetric representation, the integral need not be evaluated, as already discussed in the context of Figure 6.7. This point is further discussed in the context of transition dipole moments in Section 14.5. Note that we use the language ‘contains’ the totally symmetric representation to account for cases where the product of the irreps is a linear combination of irreps, any one of which is the totally symmetric one.
Finally, recall that the presence of certain symmetry elements reduces the rotational partition function as described in Section 10.3.5 and Table 10.1. In addition, if a molecule can adopt the same conformation (to within enantiomerism) using different values for internal degrees of freedom, then this ‘structural degeneracy’ contributes to the free energy a term of −RT lnn where n is the number of otherwise identical conformations that employ different values for the internal degrees of freedom. For example, the two conformations of 1,2- ethanediol shown in Figure B.3 belong to the C1 and C2h point groups, respectively. The former is 4-fold degenerate, while the latter has no degeneracy. This effect can be important in the evaluation of Boltzmann-averaged conformational populations in potentially symmetric molecules.

Appendix C
Spin Algebra
C.1 Spin Operators
Electrons (and many other particles) have associated with them an intrinsic angular momentum that has come to be called ‘spin’. One of the greatest successes of relativistic quantum mechanics is that spin is seen to arise naturally within the relativistic formalism, and does not need to be added post facto as it is in non-relativistic treatments. As with orbital angular momentum, spin angular momentum has x, y, and z components, and the operators Sx , Sy , and Sz, together with orthonormal eigenfunctions α and β of electron spin, are defined from
Sx α = |
21 hβ¯ |
(C.1) |
Sx β = |
21 hα¯ |
(C.2) |
Sy α = |
21 ihβ¯ |
(C.3) |
Sy β = |
− 21 ihα¯ |
(C.4) |
Szα = |
21 hα¯ |
(C.5) |
Szβ = |
− 21 hβ¯ |
(C.6) |
where i = √−1.
Thus, α and β are eigenfunctions of the operator Sz, with eigenvalues of 1/2 and −1/2, respectively, in atomic units (recall that the value of h¯ is 1 in atomic units, see Table 1.1). The spin operator S is defined by
S = Sx + Sy + Sz |
(C.7) |
and repeated application of Eqs. (C.1) through (C.6) reveals that
S2α = 21 ( 21 + 1)h¯ 2α |
(C.8) |
Essentials of Computational Chemistry, 2nd Edition Christopher J. Cramer
2004 John Wiley & Sons, Ltd ISBNs: 0-470-09181-9 (cased); 0-470-09182-7 (pbk)

566 |
|
|
|
|
APPENDIX C |
|
|
|
|
|
and |
|
|
|
|
S2β = 21 ( 21 + 1)h¯ 2β |
|
|
|
|
|
|
|
|
|
|
|
|
|
(C.9) |
||
That is, |
α |
and |
β |
are also |
eigenfunctions of the operator S2 |
with eigenvalues |
s |
s |
+1) where, |
|
|
|
1 |
|
( |
|
|||||
for a single electron, s is |
2 . |
|
|
|
|
|
||||
For an N -electron spin function, the total spin angular momentum is additive, i.e., |
||||||||||
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
S = |
|
|
|
|
(C.10) |
|
|
|
|
|
S(i) |
|
|
|
||
i=1
where S(i) is the operator of Eq. (C.7) applied to electron i. The individual Cartesian components of the spin angular momentum are also additive. Thus, for a normalized N -electron spin function , Eqs. (C.5) and (C.6) imply that
N |
|
|
|
Sz = sz(i) |
(C.11) |
i=1
where sz(i) is the eigenvalue ± 12 of the Sz operator for electron i. Thus is an eigenfunction of the z component of the total spin angular momentum with an eigenvalue equal to the sum of the eigenvalues of the individual electrons.
Consider the operator S2 for a many-electron spin function. From Eq. (C.10) and also Eqs. (C.1) to (C.6) it follows that
N N
S2 = i=1 |
S2(i) + 2 i<j Sx (i)Sx (j ) + Sy (i)Sy (j ) + Sz(i)Sz (j ) |
(C.12) |
One may ask under what circumstances are many-electron wave functions eigenfunctions of S2, and that question is addressed next.
C.2 Pureand Mixed-spin Wave Functions
For ease of notation only the two-electron case is considered here. Generalization to more electrons is entirely straightforward, if algebraically tedious. In the simplest case, both electrons are spin-paired in the same orbital, in which event we have
CSS = √2 |
a(2)α(2) |
a(2)β(2) |
|
||||
1 |
|
a(1)α(1) |
a(1)β(1) |
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
= |
√ |
|
a(1)a(2)[α(1)β(2) − α(2)β(1)] |
(C.13) |
|||
2 |
|||||||
where the superscript CSS emphasizes that is a closed-shell state and a is the normalized spatial part of the doubly occupied molecular orbital. If we evaluate S2 for this wave
SPIN ALGEBRA |
567 |
function we have
CSS |S2|CSS = 12 a2(1)a2(2) [α(1)β(2) − α(2)β(1)]|S2 |[α(1)β(2) − α(2)β(1)]
= 21 [ α(1)β(2)|S2 |α(1)β(2) − α(1)β(2)|S2 |α(2)β(1) |
|
− α(2)β(1)|S2 |α(1)β(2) + α(2)β(1)|S2 |α(2)β(1) ] |
(C.14) |
Note that since the spatial part of the molecular orbital is independent of spin, it may be integrated out (to 1). As for the remaining expectation values, if we evaluate Eq. (C.12) for the spin product function α(1)β(2) we find
S2α(1)β(2) = S2(1)α(1)β(2) + S2(2)α(1)β(2) + 2Sx (1)Sx (2)α(1)β(2)
+2Sy (1)Sy (2)α(1)β(2) + 2Sz(1)Sz(2)α(1)β(2)
=12 ( 12 + 1)α(1)β(2) + 12 ( 12 + 1)α(1)β(2) + 12 β(1)α(2) + 12 β(1)α(2)
− 21 α(1)β(2) |
(C.15) |
where we employ atomic units to avoid writing h¯ 2 repeatedly and evaluate the one-electron spin operators using Eqs. (C.1) through (C.6) and (C.8) and (C.9.) Similarly, we have
S2α(2)β(1) = 12 ( 12 + 1)α(2)β(1) + 12 ( 12 + 1)α(2)β(1) + 12 β(2)α(1) + 12 β(2)α(1)
− 21 α(2)β(1) |
(C.16) |
Using Eq. (C.15) allows us to evaluate the first integral on the r.h.s. of the last equality in Eq. (C.14) as
α(1)β(2)|S2 |α(1)β(2) = α(1)β(2) 12 ( 12 + 1)α(1)β(2)dω(1)dω(2)
+α(1)β(2) 12 ( 12 + 1)α(1)β(2)dω(1)dω(2)
+α(1)β(2) 12 β(1)α(2)dω(1)dω(2)
+α(1)β(2) 12 β(1)α(2)dω(1)dω(2)
−α(1)β(2) 12 α(1)β(2)dω(1)dω(2)
=12 ( 12 + 1) + 12 ( 12 + 1) + 0 + 0 − 12
= 1 |
(C.17) |
where the orthonormality of the α and β spin functions for each electronic spin coordinate ω permits the trivial evaluation of the individual integrals. Since the fourth integral
