Cramer C.J. Essentials of Computational Chemistry Theories and Models

low-energy systems than high-energy ones, so tunneling effects tend to predominate over non-classical reflection, and the inclusion of quantum mechanical tunneling can be critical to predicting accurate rate constants. Within a TST (or VTST) framework, one writes

where κ is called the transmission coefficient. The transmission coefficient is a function of temperature and, importantly, of the shape of the PES in the region about the activated complex. In the classical limit κ = 1 but, particularly at low temperatures, κ can become arbitrarily large.

Qualitatively, κ depends on the shape of the barrier (both height and width), the mass of the particle (the lighter the particle, the greater the probability of tunneling), and the temperature, the latter because T dictates the Boltzmann population of the reactant and activated-complex energies. In the context of a many-atom system, tunneling through the barrier may occur along any one or more coordinates, and the mass in question for each case may be considered to be the reduced mass of the normal mode. Thus, tunneling effects can be present even when the reaction coordinate itself is dominated only by heavy-atom motion.

Highly accurate prediction of transmission coefficients including many degrees of freedom is a very difficult quantum mechanical problem. A simplifying approximation is to consider tunneling only in the degree of freedom corresponding to the reaction coordinate. Within this one-dimensional formalism, various levels of approximation are available.

The simplest approximation is that of Wigner (1932), which takes

where ν‡ is the imaginary frequency associated with the reaction coordinate (the notation Im(x) means that we take only the imaginary part of the frequency, which is to say that we treat it as though it is a real number rather than a complex one). The Wigner correction works well provided that h Im(ν‡) kBT .

A more robust approximation to κ has been provided by Skodje and Truhlar (1981), generalizing earlier work by Bell (1959) for parabolic barriers. For notational convenience

where V ‡ is the zero-point-including potential energy difference between the TS structure and the reactants, and V is 0 for an exoergic reaction and the (positive) zero-point-including potential energy difference between reactants and products for an endoergic reaction. In the case where α ≤ β, the corresponding expression is

An inspection of the power series expansion for the exponential in Eqs. (15.40) and (15.41) indicates that neither expression diverges as α and β become arbitrarily close to equal (an analogous consideration of the power series expansion for the sine function in Eq. (15.40) indicates the first term on the r.h.s. to be similarly free from singularities).

A still more sophisticated approach involves fitting the reaction coordinate to a so-called Eckart potential (Eckart 1930). The Eckart potential permits an exact, analytic solution of the probability of tunneling through the barrier (and of non-classical reflection) from the time-independent Schrodinger¨ equation for systems of fixed energy E. When that result is numerically integrated over all energies, weighted by the Boltzmann probability of the reacting system having a particular energy at a given temperature T , a very good estimate of κ in the limit of tunneling along a single dimension is obtained. [Note that when transition state theory is formulated for a system of constant energy, as opposed to constant temperature, it is called microcanonical TST (µTST) or Rice –Ramsperger–Kassel–Marcus (RRKM) theory for the unimolecular case; a microcanonical variational TST (µVTST) can be applied in a fashion analogous to VTST, with the choice of dividing surface location s now potentially different at each energy E.]

It should be noted, however, that even the best one-dimensional tunneling estimate is still likely to underestimate the full tunneling contribution, since tunneling may occur through dimensions of the PES other than the reaction coordinate. Multi-dimensional tunneling approximations are sufficiently complex, however, that they will not be further discussed here.

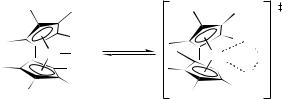
Another important point that must be borne in mind is that failure to account for tunneling, or to recognize its contribution in the first place, can lead to significant errors in the interpretation of experimental data. For example, Watson (1990) analyzed an Eyring plot of apparent rate constants for methane metathesis by methyllutetiocene (Figure 15.5) to infer

Figure 15.5 Transition-state structure for rate-determining hydrogen atom transfer in the methane metathesis reaction of methyllutetiocene. Note that the kinetics for this narcissistic reaction may be followed by using a 13C label either in the reacting methane or in the methyl group of the starting organometallic

kIn

1/T

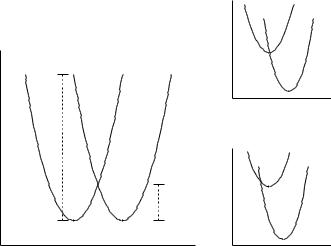
Figure 15.6 Typical changes in rate constants as a function of temperature for light-isotope (above) and heavy-isotope (below) substituted systems. In the high-temperature regime A, Arrhenius or TST plots will be essentially linear and yield good estimates of the activation parameters. In the intermediate region B, such plots may still be linear if the sampled temperature range is too small, but any activation parameters inferred therefrom will be of little utility. Additionally, KIE values in this region are very sensitive to the temperature. In the low-temperature regime C, the rate constant is almost entirely a result of tunneling, and little information about the PES can be gleaned from kinetic analysis

an activation enthalpy of 11.6 kcal mol−1. However, Sherer and Cramer (2003) found for the hydrogen-atom-transfer rate-determining step that Eqs. (15.40) and (15.41) predict the tunneling transmission coefficient κ to drop from 93 to 4 over the experimental temperature range of 300 to 400 K. When the apparent rate constants were divided by their corresponding κ values, an Eyring plot of the corrected ‘true’ semiclassical rate constants provided an activation enthalpy of 19.2 kcal mol−1. This latter result agreed well with a value of 20.3 kcal mol−1 computed from DFT, and illustrates the magnitude of the quantitative difference that may arise when tunneling is ignored in experimental Eyring analyses.

Figure 15.6 forms the basis for a more general discussion of tunneling, reaction rates, and kinetic isotope effects. The rate constant for an exergonic chemical reaction does not actually go to zero as the temperature goes to zero. Instead, after the temperature drops sufficiently, all reactant systems will be in their lowest energy state, that state will have some rate of tunneling through the barrier, and that rate is the non-zero asymptote that will be approached. Of course, an analysis that neglects tunneling would interpret a rate that is independent of temperature as corresponding to an activation enthalpy of zero (see Section 15.3.1.1) which may be very far from correct.

Moreover, because tunneling is less efficient for heavy isotopes, the transition to tunnelingdominated kinetics occurs at lower temperatures for heavier isotopes (Figure 15.6, region B),

leading to regions where KIEs will change rapidly as a function of temperature, which may also confuse interpretation. These effects are not limited to esoterically low temperatures: enzymes catalyzing proton, hydride, and hydrogen atom transfers can exhibit large rate contributions from tunneling at biological temperatures (Kohen and Klinman 1998).

15.4 Condensed-phase Dynamics

Solvent effects on reaction coordinates have already been discussed in a general fashion in Section 11.1.2. In terms of estimating condensed-phase rate constants, we consider three levels of approximation. In the simplest model, referred to as separable equilibrium solvation (SES), we assume that the effects of a surrounding condensed phase are limited simply to changing the free energy along the MEP. In that case, the condensed-phase free energy of activation is simply the sum of the gas-phase free energy of activation and the free energies of solvation of the activated complex and the reactant(s) (see Figure 11.4), and we may use Eq. (15.27) to compute the rate constant directly from the condensed-phase Go,‡. The free energy of the activated complex in solution may either be evaluated for the gas-phase TS structure, or may be taken as the maximum free energy along the solvated MEP, which would be a variational-like treatment. Operationally, we may most readily compute the solvation free energy for each point on the MEP by assuming the solvent to be fully equilibrated to that point and using any convenient solvation model (a continuum model being the most efficient choice).

At the next level of approximation, we continue to imagine the solvent to be fully equilibrated to the reacting system at every point, but instead of working with the solvated MEP from the gas-phase surface, we find the equilibrium solvation path (ESP) which is the MEP on the fully solvated surface (see Figure 11.1). While both the gas-phase and solvated surfaces are defined entirely in terms of solute coordinates, the ESP may be quite different from the gas-phase MEP because solvation effects may ‘push’ the path in directions orthogonal to the gas-phase reaction coordinate (see Figure 11.5). With the ESP in hand, TST (or VTST) analysis may be carried out in the usual way to obtain a condensed-phase rate constant.

The beauty of the prior approximations is that by assuming a mean-field influence of solvation we can continue to work in a phase space having the same dimensionality as that for the gas phase; that being the case, analysis using the tools of TST is mechanically identical for the two phases. When the solvent is not fully equilibrated with the complete reaction path, however, the reacting system can no longer legitimately be described exclusively in terms of solute coordinates.

Note that the region where solvent is least well equilibrated to the solute is expected to be in the vicinity of the activated complex, since it has so short a lifetime. Since non-equilibrium solvation is less favorable than equilibrium solvation, the non-equilibrium free energy of the activated complex is higher than the equilibrium free energy, and the non-equilibrium lag in solvent response thus slows the reaction. This effect is sometimes referred to as solvent ‘friction’ and can be accounted for by inclusion in the transmission factor κ.

Explicit inclusion of all solvent degrees of freedom, e.g., in an MD simulation, is not a very effective approach to modeling the non-equilibrium solvent influence, however. One

issue that should be apparent is that one can no longer really define a TS structure under such conditions – on the enormously high-dimensional PES constructed from all solute and solvent coordinates there will be a huge number of saddle points having similar energies in regions between reactants and products, and the related problem of running trajectories through this potentially high-energy volume of phase space to estimate rate constants has already been noted in Chapter 12.

To simplify matters, it is usually assumed that the influence of the solvent can be modeled with so-called effective solvent coordinates. A typical choice is to treat the solvent coordinate as having a harmonic potential that is linearly coupled to the solute. If one extends this approach to use an infinite number of solvent harmonic oscillators one obtains the so-called generalized Langevin equation for solute dynamics (Zwanzig 1973). In the other limit of reducing consideration of the solute to a single coordinate, one obtains Kramers–Grote –Hynes theory (Kramers 1940; Grote and Hynes 1980). The development of more sophisticated treatments for the solvent coordinates in non-equilibrium solvation models remains an active area of research.

15.5 Non-adiabatic Dynamics

15.5.1General Surface Crossings

When two (or more) potential energy surfaces corresponding to different electronic states of a chemical system are close to one another in energy, the electronic wave function should really be written as a linear combination of the different adiabatic wave functions. For simplicity, let us consider the case of only two states, in which case we would write

where ψ1 and ψ2 are the two adiabatic states that depend on the electronic coordinates q and the nuclear coordinates Q and the coefficients also depend on the nuclear coordinates because the mixing of the states will vary with different geometries. The situation is illustrated for a single internal coordinate in Figure 15.7. Note that since the coefficients c1 and c2 depend only on nuclear coordinates, each is a nuclear wave function.

In this case, the Schrodinger¨ equation becomes

where the Hamiltonian operator now includes nuclear kinetic energy as well as the nuclear repulsion, i.e.,

where mk is the mass of nucleus k in atomic units, 2 is defined as in Eq. (4.4), and Hel and VN are defined in Eq. (4.16) and the following discussion. To determine a given c as a function of nuclear coordinates Q, we can multiply both sides of Eq. (15.43) on the left

Figure 15.7 Near approach (or avoided crossing) of two electronic states as a function of nuclear coordinate Q. The inset expands the region of the avoided crossing to facilitate the definition of quantities appearing in the Landau – Zener surface-hopping-probability model

by the adiabatic state corresponding to that c and integrate. After taking advantage of the orthonormality of the adiabatic states, and noting that each adiabatic electronic wave function is an eigenfunction of the electronic Hamiltonian with an associated energy eigenvalue, we derive

where Ei is the energy eigenvalue for the ith electronic state ψi and the vector operator is defined as

Note that Eq. (15.45) is itself a Schrodinger¨ equation for nuclear eigenfunction ci . The Born–Oppenheimer approximation, previously discussed in Section 4.2.3, involves assuming a value of zero for all of the integrals in Eq. (15.45) involving the nuclear or 2 operator acting on electronic wave functions (cf. Eq. (9.37)). Under that assumption, the nuclear and electronic wave functions are separable, but spontaneous changes in electronic states, i.e., surface-to-surface crossings, are not permitted. Any model addressing such state –state interconversions must instead start from Eq. (15.45) (possibly generalized to a larger number of electronic states).

Unfortunately, Eq. (15.45) does not admit to simple analytic solutions under realistic sets of chemical conditions. Moreover, if we now try to extend Eq. (15.43) to its time-dependent

them is Marcus theory (Marcus 1964). The full scope of Marcus theory is very broad, and we consider here only the simplest application of the model. We will take the generic electron transfer reaction

For this simple case, Marcus theory predicts the rate constant for electron transfer to be

where ZAB is the collision frequency for the reactants (typically in the range of 109 to 1010 sec−1 for reactions in non-viscous liquids at ambient temperatures), GoAB is the free energy change for the electron transfer, λ is the so-called reorganization energy, R is the universal gas constant, and T is the temperature.

The reorganization energy term derives from the solvent being unable to reorient on the same timescale as the electron transfer takes place. Thus, at the instant of transfer, the bulk dielectric portion of the solvent reaction field is oriented to solvate charge on species A, and not B, and over the course of the electron transfer only the optical part of the solvent reaction field can relax to the change in the position of the charge (see Section 14.6). If the Born formula (Eq. (11.12)) is used to compute the solvation free energies of the various equilibrium and non-equilibrium species involved, one finds that

where q is the amount of charge transferred (1 for the reaction of Eq. (15.49)), ε∞ is the fast dielectric constant (sometimes called the optical dielectric constant, equal to the square of the index of refraction – around 2 for typical solvents), ε0 is the slow, or bulk, dielectric constant, rA and rB are the radii of species A and B, respectively, and rAB is the distance between them at reaction. The quantity in Eq. (15.51) is sometimes called λo because it considers only ‘outer-sphere’, which is to say solvent, reorganization. More sophisticated approaches can be used when inner-sphere reorganization is also important, e.g., for ligated metal systems where the metal–ligand bond lengths might vary significantly as a function of charge. In such instances, inner-sphere reorganization energies can often be estimated from calculations of relaxation energies when the geometry of the species for the initial charge state is allowed to relax to the final charge state.

The exact form of Eq. (15.50) is made more intuitive by considering the simple reaction coordinate diagrams of Figure 15.8. In these cases, we consider two parabolic potential energy surfaces corresponding to the two sides of Eq. (15.49). The reaction coordinate may, in particularly simple instances, be thought of as a generalized solvent coordinate. Thus, when the solvent is optimally configured for A− + B, the energy of the curve for state A + B− is quite high. If the free energies of the left and right sides of Eq. (15.49) are the same (which would happen if A and B were different isotopes of the same metal, for instance), the separation of the two curves at either minimum is exactly λ. From the mathematics of parabolae, this requires the intersection of the two curves to take place at λ/4 energy units

Figure 15.8 Electron-transfer reaction coordinate diagrams used in Marcus theory. Diagram (a) refers to a case with no net free energy of reaction, in which case the intersection of the two curves occurs at λ/4 above the minima and is taken as the barrier to the electron transfer (a barrier associated with solvent reorganization in the simplest limit). When the overall driving force is equal in magnitude to λ (b), the two curves cross at the equilibrium solvent configuration of the first state, and reaction is barrierless. However, when the driving force becomes still greater (c), the crossing of the two curves proceeds to the left on the reaction coordinate, and occurs at higher energy than the minimum of the reactant curve. This situation creates the inverted region where rate decreases with increasing exergonicity

above the two equal minima. This situation in illustrated in the first reaction coordinate diagram of Figure 15.8, and rationalizes the denominator of the exponential in Eq. (15.50): if GoAB is zero, then the argument of the exponential is λ/4RT which is indeed the ‘barrier’ for reaction in the system with no thermochemical driving force in either direction.

Note that Marcus theory in the form of Eq. (15.50) makes a rather surprising prediction. If GoAB is equal to λ in magnitude but of opposite sign, which is to say the exergonicity of the electron transfer exactly cancels the reorganization energy, than the argument of the exponential is zero and the rate is predicted to be diffusion-controlled. However, if the driving force becomes greater still, then the argument of the exponential returns to positive, and the rate is predicted to decrease (Figure 15.8). This corresponds to the so-called inverted region of Marcus theory. That is, as one of a pair of reactants in an electron-transfer reaction is varied so that the reaction becomes more and more favorable in a free-energy sense, the rate is predicted to reach a maximum and then decrease. Experimental verification of this prediction did not occur until many years after the initial publication of the theory, in part because the required driving force is so high and in part because of the technical challenges associated with measuring very large rate constants. Nevertheless, an inverted region has

now been demonstrated in several instances, and this validation of Marcus theory no doubt contributed to it being the subject of the Nobel Prize in 1992.

A key point that must be made is that quantum mechanical tunneling through the Marcustheory barrier when it is non-zero can increase the rate for electron transfer just as is true for any other activated process. Because the electron is so light a particle, tunneling can be a major contributor to the overall rate. Models for electron tunneling will not, however, be presented here.

15.6 Case Study: Isomerization of Propylene Oxide

Synopsis of Dubnikova and Lifshitz (2000) ‘Isomerization of Propylene Oxide. Quantum Chemical Calculations and Kinetic Modeling’.

When the commodity chemical propylene oxide is heated to high temperature in the gas phase in a shock tube, unimolecular rearrangement reactions occur that generate the C3H6O isomers allyl alcohol, methyl vinyl ether, propanal, and acetone (Figure 15.9). Dubnikova and Lifshitz carried out a series of calculations to determine the mechanistic pathway(s) for each isomerization, with comparison of activation parameters to those determined from Arrhenius fits to experimental rate data to validate the theoretical protocol.

Because of the complexity of the molecular hypersurface, the authors chose the B3LYP level in combination with the cc-pVDZ basis set for their search for TS structures. Based on judgment and intuition, they chose initial geometries for TS structures and optimized them subject to the constraint of there being a single imaginary frequency in the product stationary

O

acetone

O

methyl vinyl ether

Figure 15.9 Isomerizations of propylene oxide. What plausible geometries might be proposed as starting guesses for TS structures? Once a TS structure is found, will it be obvious for which process it is the TS? What features of the TS may have an impact on the level of theory used to determine its energy?