Cramer C.J. Essentials of Computational Chemistry Theories and Models

As we seek an expression for k1, we may rearrange this to

where K‡ is the equilibrium constant between the activated complex and the reactants. Using the usual relationship between free energy and the equilibrium constant, we may write

where the difference in free energy between the activated complex and the reactants is referred to as the activation free energy, G‡. Using the thermodynamic concepts of Chapter 10 (see Eqs. (10.1) and (10.3)–(10.6)), we may write the free energy of a species as

where Q is the partition function. Combining Eqs. (15.16) and (15.17) we may write.

K‡ = e−[(U‡,0 −P V‡−kB T ln Q‡ )−(UA,0 −P VA −kBT ln QA )]/ kBT

Note that the zero-point-energy-including difference in internal energies between A and A‡ in the exponential term is easily computable from an electronic structure calculation (for the electronic energy) and a frequency calculation (to determine the ZPVE) for the minimum energy and TS structures corresponding to A and A‡, respectively. In addition, the availability of frequencies for A permits ready computation of QA, as described in Chapter 10. Some attention needs to be paid, however, to the nature of the partition function for the activated complex, Q‡.

Following up on the discussion in Section 15.2 about the nature of the activated complex, the TS structure should be recognized as a species that is a minimum in 3N − 7 degrees of freedom – the ‘missing’ degree of freedom is the reaction coordinate. Thus, we may readily define the electronic, translational, and rotational components of the partition function associated with the TS structure in the usual way. For the vibrational component, we will separate

out the partition function for the reaction coordinate degree of freedom (see Eq. (10.28)) and write

where Q‡ is the reduced partition function over the 3N − 7 bound degrees of freedom and ω‡ is the ‘vibrational frequency’ associated with the reaction coordinate. If we use a power series expansion for the exponential function of ω‡ on the r.h.s. of Eq. (15.20), truncating after the first two terms, we have

Notice that the only two unknowns remaining are k‡ and ω‡. In this case, the vibrational frequency ω‡ should not be thought of as the imaginary frequency that derives from the standard harmonic oscillator analysis, but rather the real inverse time constant associated with motion along the reaction coordinate. However, it is exactly motion along the reaction coordinate that converts the activated complex into product B. That is, k‡ = ω‡. Eliminating their ratio of unity from Eq. (15.21) leads to the canonical TST expression

For the bimolecular reaction case involving reactants A and B, the derivation above generalizes to

A point of occasional confusion arises with respect to units. In Eq. (15.22), all portions are unitless except for kBT / h, which has units of sec−1, entirely consistent with the units expected for a unimolecular rate constant. In Eq. (15.23), the same is true with respect to the r.h.s., but a bimolecular rate constant has units of concentration−1 sec−1, which seems paradoxical. The point is that, as with any thermodynamic quantity, one must pay close attention to standard-state conventions. Recall that the magnitude of the translational partition function depends on specification of a standard-state volume (or pressure, under ideal gas conditions). Thus, a more complete way to write Eq. (15.23) is

where the various Qo terms have values of one and carry the standard-state volume units used for the translational partition function (the same generalization applies to Eq. (15.22),

computed for any temperature within the range of the data points and compared directly to a theoretical computation of this quantity (extrapolation outside the range of the data points can be dangerous because enthalpy and entropy are themselves both dependent on temperature, so it represents an approximation to assume their constancy over a given measurement range).

An alternative analysis having a long history, however, is to simply plot ln k vs. 1/T , this

where A is the so-called pre-exponential factor and Ea is the Arrhenius activation energy. Rearranging Eq. (15.30) readily illustrates that a plot of ln k vs. 1/T will have slope −Ea/R and intercept ln A. Simple algebra allows us to express the relationships between the Arrhenius quantities and the thermodynamic quantities as

Because these two different conventions exist (as well as other conventions, e.g., one based on collision theory, that will not be discussed here), when the term ‘activation energy’ is used without qualification, it is critical for accurate comparisons that it be established whether this term refers to an Arrhenius activation energy, a TST activation free energy, a difference in stationary-point potential energies, a difference in zero-point-including stationary-point potential energies, etc. The term ‘barrier’ is also often used ambiguously, and care should be taken to establish its meaning in a given situation.

One point of interest deriving from the equations of TST (and Arrhenius theory) is that the upper limit for the 298 K rate constant of a unimolecular reaction that takes place with zero activation energy (of whatever sort) is roughly 1013 sec−1. This is, in some sense, a conceptually obvious result since that is on the order of a molecular vibrational frequency, which is thought of as the ‘mechanism’ by which a transition state goes to its products.

15.3.1.2 Kinetic isotope effects

As noted in Chapter 10, the zero-point energy, and the translational, rotational, and vibrational partition functions all depend on the isotopic masses of the atoms. Thus, so too does the rate constant for a given reaction. A difference in rates observed for two different isotopically substituted reactants is referred to as a kinetic isotope effect (KIE), usually expressed as a ratio of rates. Isotope effects are divided into two classes: primary isotope effects refer to situations where the isotopic substitution involves one of the two atoms involved in a

breaking (or making) bond, while secondary isotope effects cover all other possibilities. In general, then, a KIE may be computed as

QR,heavy

‡

= Qlight QR,heavy e−( ZPVE‡light − ZPVE‡heavy)/ kBT (15.33) Q‡heavy QR,light

From a theoretical perspective, isotope effects are fairly trivially computed. The stationary points on the PES and their electronic energies are independent of atomic mass, as are the molecular force constants. Thus, one simply needs to compute the isotopically dependent zero-point energies and translational, rotational, and vibrational partition functions, and evaluate Eq. (15.33).

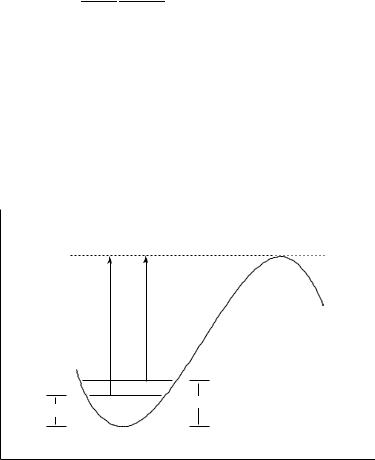
Primary isotope effects tend to be dominated by the difference in zero-point energies, as illustrated in Figure 15.2. Because the reaction coordinate is the breaking bond, and because there is little or no ZPVE associated with this mode in the TS structure, the full difference in reactant ZPVEs enters into the difference in zero-point-including potential energy barriers.

Reaction coordinate

Figure 15.2 The dominant contribution to a primary KIE is the differential loss of zero-point vibrational energy in the reaction coordinate when an isotopically substituted bond is broken. Because the light isotopomer has a higher vibrational frequency, it has more ZPVE, and a lower potential energy of activation (thus primary isotope effects expressed as klight/kheavy are essentially always greater than 1). Effects from other normal modes are ignored in this diagram (cf. Figure 15.3)

To a rough approximation, then, in the limit of a fully broken bond in the TS structure, the primary KIE is

kheavy

where ωR,‡ refers to the frequency in the reactants of the bond being broken in the TS structure. One of the largest possible differences in isotopic frequencies involving elements occurs for hydrogen/deuterium substitutions, with X–H bonds typically having stretching frequencies about 35% larger than X–D bonds. Using this relationship and a light isotope frequency of 3100 cm−1, Eq. (15.34) suggests that the maximum primary KIE for a hydrogen/deuteriumsubstituted system at 298 K is about 7. Of course, if the bond is not fully broken in the TS structure, smaller values may be observed/computed. Larger values may also be observed, owing to quantum mechanical tunneling, as described in Section 15.3.3. When heavier elements are used, isotope effects become smaller, but a number of experimental techniques have proven to be sufficiently accurate to measure very small differences (see, for instance, Keating et al. 1999).

Secondary KIEs are also typically much smaller than primary KIEs, because the isotopically substituted modes are not lost in the TS structure (see Figure 15.3). In addition,

12 hw‡light 12 hw‡heavy

∆V ‡heavy ∆V ‡light

E

Reaction coordinate

Figure 15.3 Secondary KIEs are associated with normal modes other than the reaction coordinate, one of which is shown in this diagram. The heavy and light vibrational frequencies both change on going from the reactant (R) to the TS structure (‡); because in this example the mode is ‘tighter’ in the TS structure, the difference between the heavy and light ZPVEs increases, and this causes the potential energy of activation to be larger for the light isotopomer than the heavy one (an example of an inverse secondary KIE). In a real many-atom system there are potentially a large number of modes that will contribute to the secondary KIE, some in a normal fashion and some in an inverse fashion

secondary KIEs can be ‘inverse’, which is to say that the light atom rate over the heavy atom rate can be less than one. In this case, no particular simplifications of Eq. (15.33) are general, and each partition function may play a role in addition to those of the ZPVEs. This is particularly true because different vibrational modes may cancel one another in the secondary KIE. That is, one mode may lead to a large normal KIE but be canceled by another mode that leads to a large inverse KIE, such that more subtle effects associated with, say, rotational motion, may be made manifest.

One caveat that must be observed when comparing computed and experimental isotope effects is that experimental measurements can sometimes be for multistep reactions. When a particular elementary reaction is not rate-determining, that is, it is not the bottleneck in the overall process, then it does not matter whether or not that reaction has associated with it a large KIE; it will not influence the observed overall rate. A separate caveat with light atoms at low to moderate temperatures is that tunneling effects may play a significant role.

15.3.2Variational Transition-state Theory

Canonical TST defines the free energy of the activated complex based on the TS structure. This is convenient because, as it is a stationary point, we can use the machinery of the rigid-rotor-harmonic-oscillator approximation to compute the necessary partition functions to define its (reduced-dimensionality) free energy. However, it is by no means guaranteed that the free energy associated with the TS structure really is the highest free energy of any point along the MEP – it is only guaranteed that it is the highest point of potential energy along the MEP. As a simple example, it might be the case that the potential energy wells associated with some normal modes tighten up after the TS structure is reached, even though the bottoms of those wells are at a point on the MEP slightly below the energy of the TS structure. The increase in ZPVE resulting from those tighter potentials may exceed the drop in bottom-of-the-well energy such that the free energy of the non-stationary point is higher than that of the TS structure.

Variational transition-state theory (VTST), as its name implies, variationally moves the reference position along the MEP that is employed for the computation of the activated complex free energy, either backwards or forwards from the TS structure, until the rate constant is minimized. Notationally

where s is a position on the MEP at which kVTST is evaluated. By convention, s = 0 refers to the saddle point, and negative and positive values are displaced to the reactant and product sides of the saddle point, respectively.

To compute the r.h.s. of Eq. (15.35), we need to define how we compute the partition function (and the ZPVE) for the non-stationary point s. In this case, we simply continue to take advantage of our decision to treat the activated complex as a species having 3N − 7 bound degrees of freedom. In order to define this space for an arbitrary point on the MEP,

we simply project out motion along the MEP at point s and evaluate the partition functions (and the ZPVE) for the remaining degrees of freedom, all of which are bound and at their local minima for that choice of s, in the usual fashion. In practice, minimization of the rate constant with respect to s is accomplished by standard search techniques for situations where analytic gradients of the function to be minimized are not available. Since the partition functions depend on both s and T , changes in T may lead to changes in the value of s minimizing Eq. (15.35). In other words, the variational transition state can move with changes in temperature.

Such detailed surveys of the potential energy surface are computationally fairly demanding since not only are energies sought at every point but also gradients (to assess the degree to which one is still on the MEP) and force constants for all bound degrees of freedom (to compute the vibrational partition functions). If the potential energy surface for the reacting system can be described by an analytic function, then the computational complexity is not much worse than for any typical propagation of a molecular mechanics MD trajectory. However, while molecular mechanics can accurately describe regions of the PES in the close vicinity of minima, it is much more difficult to develop analytic functions for regions within which bond breaking (or making) are taking place and, moreover, to connect any such functions to the ‘usual’ ones about minima so that the entire PES can be described in a smooth, differentiable way.

One alternative to having a global analytic function is simply to compute, on the fly, energies, derivatives, and force constants whenever they are required. Such an approach, usually called ‘direct dynamics’ (Truhlar and Gordon 1990), in principle permits the use of sophisticated quantum mechanical methods at every point. While this will typically improve on the quality of the computed quantities compared to a global analytic function, this improvement comes at the expense of potentially having to do many, many such QM calculations (this latter point is especially telling when one is actually propagating a trajectory, as opposed to simply looking for the variational TS). These constraints have provided much of the motivation for the development of rapid MM and QM/MM models, like the MCMM and VB methods discussed in Chapters 2 and 13, that can accurately reproduce features of the PES in the vicinity of TS structures, where VTST optimization takes place.

Note that the conventional TST expression is simply the special case of VTST where evaluation is done exclusively for s = 0. As such, the VTST rate constant will always be less than or equal to the conventional TST rate constant (equal in the event that s = 0 minimizes Eq. (15.35)). Put differently, when very accurate potential energy surfaces are available, the conventional TST rate constant is typically an overestimate of the exact classical rate constant. (Note that it is possible, however, for a compensating or even offsetting error to arise from overestimation of the barrier height if the potential energy surface is not very accurate.)

Allison and Truhlar have compared TST and VTST to accurate solution of the timedependent Schrodinger¨ equation for a number of three-atom chemical reactions (it is only for such small systems that the accurate solution of the time-dependent Schrodinger¨ equation is practical) and those results are listed in Table 15.1. On the high-quality surfaces available for this comparison, VTST is typically accurate to within 50% at temperatures above 600 K.

Table 15.1 Logarithmically averaged percent errors in TST and VTST compared to accurate quantal rate constants for a series of 3-atom reactionsa

a Allison and Truhlar 1998. Logarithmically averaged percent errors treat each factor of 2, whether an overestimate or an underestimate, as a 100% error.

At the highest temperatures, VTST is about five times more accurate than canonical TST, but even canonical TST is still accurate to within about a factor of 2. Note that improved performance of VTST as temperature increases is to be expected since entropic effects increasingly dominate under those conditions, and it is primarily entropy that moves the optimal dividing surface away from the potential energy saddle point. At low temperatures, TST appears to outperform VTST, but that is an artifact of not considering tunneling contributions to the rate constant (see Section 15.3.3). Tunneling effects are included in the accurate quantal rate constants; since TST usually overestimates the classical rate, it is accidentally in better agreement with the quantal rate, which is always increased over the exact classical rate by tunneling.

Note that, with the minimized rate constant in hand, a generalized activation free energy can be defined as the difference between the free energy of the reactants and that for the point smin. Note also that for the computation of isotope effects, VTST proceeds exactly like conventional TST, except that there is no requirement at a given temperature that the value of s that minimizes the rate constant for the light-atom-substituted system will be the same value of s that minimizes the rate constant for the heavy-atom-substituted system. Each must be determined separately, at which point the ratio of rate constants for that temperature may be expressed.

15.3.3Quantum Effects on the Rate Constant

The metaphor invoked in Section 15.2 of a reacting system as a cloud wandering through a mountain pass is, by virtue of being macroscopic, necessarily a classical metaphor. In visualizing that situation, we accept as a given that those portions of the cloud below the level of the pass (i.e., at too low an energy) fail to go through and portions above the pass always do. Like the cloud in the mountain pass, the probability of transmission from

reactants to products in a classical system is a Heaviside function of the energy, as illustrated in Figure 15.4. In a quantum system, however, the transmission probability is sigmoidal in shape, reflecting the phenomena of tunneling and non-classical reflection. Tunneling refers to the ability of a quantum system having an energy below the saddle point to ‘tunnel’ through the barrier to the products side, while non-classical reflection refers to the possibility that a quantum system above the saddle-point energy will suffer from destructive interference in a way that prevents it from crossing to products. This situation is compared to the classical one in Figure 15.4.

Insofar as tunneling increases the rate constant by allowing lower-energy systems to be reactive and non-classical reflection decreases the rate constant by reducing the reactivity of higher-energy systems, one might imagine that the two could safely be assumed to cancel. However, a thermally equilibrated Boltzmann population has a much larger percentage of

Reactant energy

Figure 15.4 Probabilities of reaction (P ) for systems moving towards a parabolic barrier for a reaction with a zero-point-including potential energy of activation V ‡. Classical systems ( ) below the barrier height have zero probability of reaction and above the barrier height have unit probability (i.e., the ‘curve’ describes a Heaviside function). Quantum systems (- - - - - - ), on the other hand, have increasingly non-zero probabilities as the barrier energy is approached from below because of tunneling and increasingly less than unit probabilities as the barrier energy is approached from above because of non-classical reflection. Note that because of the Boltzmann distribution of energies in a thermalized population of reacting systems (-· -· -· -· referenced to the right ordinate), typically many more molecules have energies in the region where tunneling can increase the reaction rate than have energies in the region where non-classical reflection can reduce the reaction rate. As a result, the former is the more quantitatively important of the two quantum phenomena