Cramer C.J. Essentials of Computational Chemistry Theories and Models

484 13 HYBRID QUANTAL/CLASSICAL MODELS

A key point made by the authors is that the neglect of quantum effects in purely classical simulations, particularly zero-point vibrational energy, can have very large effects on computed kinetic quantities. Thus, when the free energy of activation is computed using the QM/MM potential energies but a purely classical formalism for the vibrational partition function (i.e., by using a continuous integral in place of the discrete sum that is used for a QM harmonic oscillator; see Eq. (10.26)), the rate is underestimated by a factor of 34 compared to the complete QM/MM prediction. A still larger discrepancy is seen in the kinetic isotope effect: the purely classical treatment of vibrations predicts a KIE of 1.3, while the fully QM/MM protocol predicts 3.5 after accounting for a small tunneling effect. The latter method is in much better agreement with the experimental value of 3.3.

Having successfully matched the several experimental observables available for the enolase system, Alhambra and co-workers then examine the reaction coordinate to better understand the factors discriminating H from D reactivity. They discover that the TS for the reaction of H is much later than that for reaction of D, because the rapidly increasing zeropoint energy of the N – H bond compared to the N – D bond offsets the drop in reaction coordinate potential energy and moves the free-energy bottleneck for H further towards products.

The authors finish by predicting a quantity that has not yet been measured, the secondary KIE that would be obtained with – ND2 in place of – NH2 as the reactive base. They also note the critical role of the Mg2+ counterions in facilitating the reaction. The binding to the two cations of the phosphoenolpyruvate tetraanion compared to the reactant trianion is predicted to be increased by some 240 kcal mol−1; this offsets the highly unfavorable pKa of the C-2 proton sufficiently to render the overall reaction thermochemistry only 2.8 kcal mol−1 endergonic.

One difficulty associated with the authors’ methodology is that, in the absence of having substantial experimental data in hand, it is not in general obvious that a random selection of a frozen MM structure from an equilibrated trajectory will provide a useful configuration. In this instance, the authors were able to validate the quality of their framework geometry and go on to perform more in depth analyses of microscopic features of the reaction; an a priori prediction of the reaction’s free-energy profile, however, would require a more complicated consideration of an ensemble of structures. A detailed protocol for such an endeavor was subsequently described (Alhambra et al. 2001), and has been applied to other systems.

Bibliography and Suggested Additional Reading

Aqvist,˚ J. and Warshel, A. 1993. ‘Simulation of Enzyme Reactions Using Valence Bond Force Fields and Hybrid Quantum/Classical Approaches’, Chem. Rev., 93, 2523.

Elstner, M., Frauenheim, T., Kaxiras, E., Seifert, G., and Suhai, S. 2000. ’A Self-consistent Charge Density-functional Based Tight-binding Scheme for Large Biomolecules’, Phys. Stat. Sol. B, 217, 357.

Field, M. J. 2002. ’Simulating Enzyme Reactions: Challenges and Perspectives’ J. Comput. Chem., 23, 48.

Gao, J. 1996. ‘Methods and Applications of Combined Quantum Mechanical and Molecular Mechanical Potentials’, in Reviews in Computational Chemistry , Vol. 7, Lipkowitz, K. B. and Boyd, D. B., Eds., VCH: New York, 119.

Method for the Treatment of Boundary Atoms in Combined QM/MM Calculations’, J. Phys. Chem. A, 102, 4714.

Gao, J. and Thompson, M. A., Eds., 1998. Methods and Applications of Hybrid Quantum Mechanical and Molecular Mechanical Methods, ACS Symposium Series, Vol. 712, American Chemical Society: Washington, DC.

Orozco, M. and Luque, F. J. 2000. ‘Theoretical Methods for the Description of the Solvent Effect on Biomolecular Systems’, Chem. Rev., 100, 4187.

Reuter, N., Dejaegere, A., Maigret, B., and Karplus, M. 2000. ‘Frontier Bonds in QM/MM Methods: A Comparison of Different Approaches’, J. Phys. Chem. A, 104, 1720.

Ryde, U. 2003. ‘Combined Quantum and Molecular Mechanics Calculations on Metalloproteins’ Curr. Opin. Chem. Biol., 7, 136.

Thery,´ V., Rinaldi, D., Rivail, J.-L., Maigret, B., and Ferenczy, G. G. 1994. ‘Quantum Mechanical Computations on Very Large Molecular Systems: The Local Self-consistent Field Method’, J. Comput. Chem., 15, 269.

Warshel, A. 1991. Computer Modeling of Chemical Reactions in Enzymes and in Solutions, Wiley: New York.

Zhang, Y. K., Lee, T. S., and Yang, W. T. 1999. ‘A Pseudobond Approach to Combining Quantum Mechanical and Molecular Mechanical Methods’, J. Chem. Phys., 110, 46.

References

Abraham, R. J. and Siverns, T. M. 1972. Tetrahedron, 28, 3015.

Alhambra, C., Gao, J., Corchado, J. C., Villa,` J., and Truhlar, D. G. 1999. J. Am. Chem. Soc., 121, 2253.

Alhambra, C., Corchado, J., Sanchez,´ M. L., Garcia-Viloca, M., Gao, J., and Truhlar, D. G. 2001.

J. Am. Chem. Soc., 105, 11326.

Amara, P. and Field, M. 2003. Theor. Chem. Acc., 109, 43.

Amara, P., Field, M. J., Alhambra, C., and Gao, J. 2000. Theor. Chem. Acc., 104, 336. Aqvist,˚ J. and Warshel, A., 1992. J. Mol. Biol., 224, 7.

Bakowies, D. and Thiel, W. 1996. J. Phys. Chem., 100, 10580.

Bandyopadhyay, P., Gordon, M. S., Mennucci, B., and Tomasi, J. 2002. J. Chem. Phys., 116, 5023. Banks, J. L., Kaminski, G. A., Zhou, R. H., Mainz, D. T., Berne, B. J., and Friesner, R. A. 1999. J.

Chem. Phys., 110, 741.

Chambers, C. C., Giesen, D. J., Hawkins, G. D., Vaes, W. H. J., Cramer, C. J., and Truhlar, D. G. 1999. In: Rational Drug Design, Truhlar, D. G., Howe, W. J., Hopfinger, A. J., Blaney, J. M., and Dammkoehler, R. A., Eds., Springer: New York, 51.

Chandrasekhar, J., Shariffskul, S., Jorgensen, W. L. 2002. J. Phys. Chem. B, 106, 8078. Chang, Y.-T., Minichino, C., and Miller, W. H. 1992. J. Chem. Phys., 96, 4341. Corchado, J. C. and Truhlar, D. G. 1998. J. Phys. Chem. A, 102, 1895.

Cramer, C. J., and Pak, Y. 2001. Theor. Chem. Acc., 105, 477. Cramer, C. J. and Truhlar, D. G. 1992. Chem. Phys. Lett., 198, 74.

Cramer, C. J. and Truhlar, D. G. 1993. Chem. Phys. Lett., 202, 567 (erratum). Cui, Q. 2002. J. Chem. Phys., 117, 4720.

Deng, L., Woo, T. K., Cavallo, L., Margl, P. M., and Ziegler, T. 1997. J. Am. Chem. Soc., 119, 6177. Depaepe, J.-M. and Ryckaert, J.-P. 1995. Chem. Phys. Lett., 245, 653.

Eurenius, K. P., Chatfield, D. C., Brooks, B. R., and Hodoscek, M. 1996. Int. J. Quantum Chem., 60, 1189.

Ferenczy, G. G., Rivail, J.-L., Surjan,´ P. R., and Naray´-Szabo,´ G. 1992. J. Comput. Chem., 13, 830.

486 13 HYBRID QUANTAL/CLASSICAL MODELS

Florian,´ J. and Warshel, A. 1997. J. Phys. Chem. B, 101, 5583. Freedman, H. and Truong, T. N. 2003. Chem. Phys. Lett., 381, 362. Freindorf, M. and Gao, J. 1996. J. Comput. Chem., 17, 386.

French, A. D., Kelterer, A.-M., Cramer, C. J., Johnson, G. P., and Dowd, M. K. 2000. Carbohydr. Res., 326, 305.

Gao, J. 1994. J. Am. Chem. Soc., 116, 1563.

Gao, J. and Xia, X. 1992. Science, 258, 631.

Gao, J., Amara, P., Alhambra, C., and Field, M. J. 1998. J. Phys. Chem. A, 102, 4714. Garcia-Viloca, M. and Gao, J. 2004. Theor. Chem. Acc., 111, 280.

Humbel, S., Sieber, S., and Morokuma, K. 1996. J. Chem. Phys., 105, 1959. Kaminski, G. and Jorgensen, W. L. 1996. J. Phys. Chem., 100, 18010. Kaminski, G. and Jorgensen, W. L. 1998. J. Phys. Chem. B, 102, 1787. Kerdcharoen, T. and Morokuma, K. 2002. Chem. Phys. Lett., 355, 257.

Kim, Y., Corchado, J. C., Villa,` J., Xing, J., and Truhlar, D. G. 2000. J. Chem. Phys., 112, 2718. Kongsted, J., Osted, A., Mikkelsen, K. V., Christiansen, O. 2003. J. Phys. Chem. A, 107, 2578. Lee, P. H. and Maggiora, G. M. 1993. J. Phys. Chem., 97, 10175.

Loeffler, H. H., Yague, J. I., and Rode, B. M. 2002. J. Phys. Chem. A, 1106, 9529. Luzhkov, V. and Warshel, A. 1992. J. Comput. Chem., 13, 199.

Martin, M. E., Aguilar, M. A., Chalmet, S., Ruiz-Lopez,´ M. F. 2002. Chem. Phys., 284, 607. Maseras, F. and Morokuma, K. 1995. J. Comput. Chem., 16, 1170.

Matsubara, T., Maseras, F., Koga, N., and Morokuma, K. 1996. J. Phys. Chem., 100, 2573. Mo, Y. and Gao, J. 2000. J. Phys. Chem. A, 104, 3012.

Papazyan, A. and Warshel, A. 1997. J. Phys. Chem. B, 101, 11254. Philipp, D. M. and Friesner, R. A. 1999. J. Comput. Chem., 20, 1468. Pratt, L. R. and Chandler, D. C. 1977. J. Chem. Phys., 67, 3683.

Pu, J., Gao, J., and Truhlar, D. G. 2004. J. Phys. Chem. A, 108, 632.

Rickard, G. A., Karadakov, P. B., Webb, G. A., and Morokuma, K. 2003. J. Phys. Chem. A, 107, 292. Shao, L., Yu, H. A., and Gao, J. L. 1998. J. Phys. Chem. A, 102, 10366.

Sherer, E. C. and Cramer, C. J. 2001. J. Comput. Chem., 22, 1167.

Svensson, M., Humbel, S., and Morokuma, K. 1996. J. Chem. Phys., 105, 3654.

Svensson, M., Humbel, S., Froese, R. D. J., Matsubara, T., Sieber, S., and Morokuma, K. 1996. J. Phys. Chem., 100, 19357.

Swart, M. 2003. Int. J. Quant. Chem., 91, 177.

Ten-no, S., Hirata, F., and Kato, S. 1993. Chem. Phys. Lett., 214, 391.

Udier-Blagovic, M., Morales de Tirado, P., Pearlman, S. A., and Jorgensen, W. L. 2004. J. Comput. Chem., 25, 1322.

Vreven, T., Mennucci, B., da Silva, C. O., Morokuma, K., and Tomasi, J. 2001. J. Chem. Phys., 115, 62.

¨

Vreven, T., Morokuma, K., Farkas, O., Schlegel, H. B., Frisch, M. J. 2003. J. Comput. Chem., 24, 760. Warshel, A. and Levitt, M. J. 1976. J. Mol. Biol., 103, 227.

Warshel, A. and Weiss, R. M. 1980. J. Am. Chem. Soc., 102, 6218.

Wiberg, K. B., Keith, T. A., Frisch, M. J., and Murcko, M. 1995. J. Phys. Chem., 99, 9072. Zhang, Y., Lee, T.-S, and Yang, W. 1999. J. Chem. Phys., 110, 46.

E

Figure 14.1 The singly excited state on the right may be qualitatively viewed as deriving from movement of an electron out of the ground-state HOMO into the indicated higher energy orbital (perhaps following absorption of a photon carrying the appropriate quantum of energy). Note, however, that the optimized orbitals of the ground state are at best approximations to those of the excited state

spin function. However, as described in more detail in Section 14.4 and Appendix C, the Slater determinant of Eq. (14.2) is not a pure spin state, but is instead an equal mixture of singlet and triplet states (the triplet being the so-called ‘up-down’ or ‘Sz = 0’ triplet). It turns out that the corresponding pure spin states in this instance cannot be written as single Slater determinants, rather they require a linear combination of two. It is again somewhat cumbersome, however, constantly to specify the spin state rigorously in this manner, so for ease of presentation we will simply specify the spin state in a shorthand fashion, as a left superscript on the wave function, taking as implicit that the correct wave function uses the proper linear combination of determinants and is not a single determinant as written, i.e.,

is the singlet wave function generated from the appropriate combination of determinants having electrons of opposite spin singly occupying orbitals N /2 and a and

is the analogous triplet. Following the general notational scheme already introduced in Chapter 7, we will use the right suband superscripts in ia to indicate a state generated by removing one electron from occupied orbital i and placing it into previously empty orbital a.

14.1DETERMINANTAL/CONFIGURATIONAL REPRESENTATION OF EXCITED STATES 489

Having dispensed with notational details, let us think more carefully about the chemical picture implied by Figure 14.1. By picturing an excited state as being a different occupation of the orbitals of the ground state, we are providing something of a privileged status to the ground-state orbitals. One must recall that these orbitals, in the HF procedure, are variationally optimized given an average electrostatic repulsion that depends on the shape and occupation number of all of the other MOs. When the excited state of Figure 14.1 is generated, the occupation number of the HOMO is reduced by 1 and the occupation number of the newly occupied orbital is increased by 1, and thus the HF field acting on every orbital has changed. This means that none of the occupied orbitals are optimal for the excited state, and as a result the energy of the excited state, e.g.,

evaluated using Eq. (14.3) for the wave function (i.e., the Slater determinant formed from the optimized orbitals for the ground state), will be unphysically too high.

It is somewhat tempting to impose an incorrect dynamical view on the excited state when it is generated by ground-state absorption of a photon. One might imagine that the ‘instantaneous’ absorption process generates the wave function of Eq. (14.3), which then relaxes to the optimal wave function for the excited state by adjustment of all of the orbitals. This physical picture, however, ignores the common timescale of all electronic motion. Even as the electron is ‘moving’ from one orbital to the next, the orbitals whose occupation numbers are not changing are relaxing in response to changing electron–electron interactions.

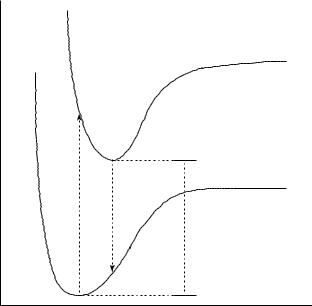
To digress for a moment, a timescale separation that usually is valid is the Born– Oppenheimer separation of the nuclear and electronic motions. Thus, as illustrated in Figure 14.2, when the optimal geometry of the ground state is not the same as that for the excited state, we may view the absorption of radiation as taking place at the ground-state geometry, and the energy involved is called the ‘vertical’ excitation energy. On the timescale of nuclear dynamics, the geometry of the excited state ultimately relaxes to its own optimum. The energy difference E between the two systems taking each to be at its own optimal geometry is referred to as the ‘adiabatic’ excitation energy. The same conceptual framework may be applied to the reverse process, emission. Note that excitation and emission energies are often expressed not in energy units but instead in terms of the wavelength of radiation corresponding to that energy according to

where h is Planck’s constant, c the speed of light in a vacuum, and λ the radiation wavelength. A larger E value is equivalent to a shorter wavelength, so one says that vertical excitations are blue-shifted (since blue light is on the short wavelength side of the visible spectrum) relative to adiabatic excitation energies, while vertical emissions with smaller E values are red-shifted (red being at the opposite end of the visible spectrum) relative to the same adiabatic standard. The difference between the vertical excitation and emission energies (or wavelengths) is referred to as the Stokes shift.

Generic coordinate

Figure 14.2 Schematic relationship between vertical absorption and emission energies and the adiabatic energy difference between the ground and excited states. [Note that a more rigorous treatment requires inclusion of ZPVE and thermal contributions in the adiabatic energy difference, and consideration of Franck – Condon overlap between quantized vibrational states for the vertical processes; some of these points are discussed in Section 14.5.]

In terms of computing adiabatic energy differences, if the Born–Oppenheimer PES for the excited state can be computed, geometry optimization of that state may be carried out using standard techniques. But, as we have been discussing above, we have not yet devised a scheme for computing the excited-state surface, since ground-state orbitals are not appropriate for minimum-determinantal excited-state wave functions. How then to obtain a better excitedstate wave function?

The simplest approach, of course, is to maintain the minimum-determinantal description and reoptimize all of the orbitals. In practice, however, such an approach is practical only in instances where the ground-state and the excited-state wave functions belong to different irreducible representations of the molecular point group (cf. Section 6.3.3). Otherwise, the variational solution for the excited-state wave function is simply to collapse back to the ground-state wave function! And, even if the two states do differ in symmetry, the desired excited state may not be the lowest energy such state within its irrep, to which variational optimization will nearly always lead.

In certain favorable instances, one can coax the SCF equations to converge to different determinants of the same electronic state symmetry. For instance, phenylnitrenes have two different closed-shell singlet states, as re-illustrated in Figure 14.3 (cf. Section 8.5.3),

14.1DETERMINANTAL/CONFIGURATIONAL REPRESENTATION OF EXCITED STATES 491

out-of-plane p orbital belonging to b2 irreducible representation

Figure 14.3 Electronic configurations of phenylnitrene, differing in occupation of the nitrogen p orbitals, labeled according to their spin and spatial symmetries. Relative energy orderings for the four configurations are indicated in parentheses; T0 is the triplet ground state, and Sn represents the nth lowest singlet excited state

differing in whether the occupied nitrogen p orbital is in the plane of the aromatic ring (S2) or perpendicular to it and conjugated with the π system (S3). As both states are closedshell, both belong to the totally symmetric irreducible representation (e.g., the two states are 1A1 since phenylnitrene belongs to the C2v point group), but the different symmetries of the alternative lone pair orbitals (one being b1 and the other b2) makes it relatively straightforward to converge variationally optimized wave functions that may be written as

(for HF example, see Kim, Hamilton, and Schaefer 1992; for corresponding DFT example, see Smith and Cramer 1996; Johnson and Cramer 2001). Note that in this case the ellipsis in each wave function carries a subscript to emphasize that while the orbitals thereby implied in Eqs. (14.7) and (14.8) are qualitatively similar, they are not identical (since each set was variationally optimized subject to different HOMOs). This point is not merely technical, but represents a critical problem associated with the approach, namely that there is no guarantee that the two wave functions of Eqs. (14.7) and (14.8) are orthogonal, as they should be.

The issue of orthogonality is an important one. Every excited state must be orthogonal to the ground state (as well as to all of the other excited states), and any technology for

describing excited states that fails to enforce such orthogonality must be viewed with caution. One might, of course, be tempted to say that the failure of an excited state to be orthogonal to the ground state would be sufficiently damning to warrant no further use of the excited-state wave function. However, there is some room for ambiguity, insofar as the excited-state wave function must be orthogonal to the exact ground-state wave function, but we are almost never working with that wave function, only some approximation thereto. Thus, an exact excitedstate wave function may very well fail to be orthogonal to, say, the HF approximation to the ground-state wave function.

In some cases, orthogonality is ensured by the individual natures of the two states. As already alluded to above, if the electronic states belong to two different irreps of the molecular point group, and the product of the two irreps fails to contain the totally symmetric representation, then the two states are necessarily orthogonal (see Appendix B). Taking again the phenylnitrene system in Figure 14.3 as an example, the lowest energy singlet is open-shell and has a single electron occupying each of the two nitrogen p orbitals. By analogy to Eqs. (14.3), (14.7), and (14.8), this formally two-determinantal wave function is

where the k subscripts on all orbitals emphasize their possible differences with those optimized for the wave functions of Eqs. (14.7) and (14.8). The electronic state symmetry of Eq. (14.9) is 1A2. Since the product of A2 with A1 in the C2v point group is A2, which is not the totally symmetric representation, the orthogonality of the A2 wave function of Eq. (14.9) with the A1 wave functions of Eqs. (14.7) and (14.8) is ensured.

A different guarantee of orthogonality arises if the two states in question have different spin. Continuing with the phenylnitrene system, the ground state is the triplet version of Eq. (14.9), i.e.,

Orthogonality of the singlet and triplet spin coordinates ensures that the wave function of Eq. (14.10) is orthogonal to all of those in Eqs. (14.7) –(14.9).

Methods for generating excited-state wave functions and/or energies may be conveniently divided into methods typically limited to excited states that are well described as involving a single excitation, and other more general approaches, some of which carry a dose of empiricism. The next three sections examine these various methods separately. Subsequently, the remainder of the chapter focuses on additional spectroscopic aspects of excited-state calculations in both the gas and condensed phases.

14.2 Singly Excited States

For an average molecule, there are typically one or more low-energy excited states that may be reasonably well described as valence-MO-to-valence-MO single electronic excitations, and the language of spectroscopy reflects this point. Thus certain states are referred to as n → π , π → π , etc., indicating the orbital from which the electron is excited on the left

and the orbital into which it is excited on the right. Finding wave functions for these states is sometimes facilitated by this relative simplicity of their character.

14.2.1SCF Applicability

Ideally, one would like to study excited states and ground states using wave functions of equivalent quality. Ground-state wave functions can very often be expressed in terms of a single Slater determinant formed from variationally optimized MOs, with possible accounting for electron correlation effects taken thereafter (or, in the case of DFT, the optimized orbitals that intrinsically include electron correlation effects are use in the energy functional). Such orbitals are determined in the SCF procedure.

However, the problem of variational collapse typically prevents an equivalent SCF description for excited states. That is, any attempt to optimize the occupied MOs with respect to the energy will necessarily return the wave function to that of the ground state. Variational collapse can sometimes be avoided, however, when the nature of the ground and excited states prevents their mixing within the SCF formalism. This situation occurs most commonly in symmetric molecules, where electronic states belonging to different irreducible representations do not mix in the SCF, and also in any situation where the ground and excited states have different spin.

As an example of the former, consider the electronic states of fluorovinylidene illustrated in Figure 14.4. There are two different low lying triplet states, one having A electronic state symmetry and the other A . Furthermore, within each respective irreducible representation, the states indicated are the lowest energy triplets. Thus, wave functions for each may be determined via an SCF approach. In this case, HF theory is not particularly attractive as an

Figure 14.4 Valence MO occupations for three different electronic states of fluorovinylidene. The triplet states belong to different irreducible representations of the molecular point group because the singly occupied orbitals in which they differ belong alternatively to either the a or a irreps