Cramer C.J. Essentials of Computational Chemistry Theories and Models

474 13 HYBRID QUANTAL/CLASSICAL MODELS

two QM atoms have been included in some studies and deliberately not included in others. There is no strong consensus on which, if either, approach is better.

4.Torsional energies involving two or three MM atoms and two or one QM atoms, respectively, are computed using the standard force-field formulation. Torsional energies involving one MM atom and three QM atoms have, like bond angles, been included in some studies and not in others.

5.Those MM point charges that are very close to the QM system, either coincidentally or because the capping hydrogen atoms bring electron density out to the MM boundary atoms, can have unphysically large influences on the electronic structure of the QM region, even when those portions of the Fock operator involving the basis functions of the capping atoms do not include their influence directly. As a result, some studies have zeroed charges on near-boundary atoms, others have scaled them, and still others have selectively kept and discarded particular interactions (Eurenius et al. 1996; Bakowies and Thiel 1996). There is increasing evidence that it is better to maintain all QM/MM charge interactions. Amara and Field (2003) have shown that these electrostatic interactions can be made considerably more stable by replacing MM point charges near the QM/MM boundary with spherical Gaussian charge distributions centered on the MM atoms in question.

6.All remaining terms associated with HQM/MM and HMM are calculated in the usual way according to Eq. (13.4).

The use of a hydrogen atom as a capping atom is clearly motivated by simplicity. It is a reasonable choice based on other considerations as well, however. In general, the position of the QM/MM boundary is selected so that it will not cut across any particularly polar or polarizable bonds. This in principle allows the correct separation of the two electrons in the (single) bond to the one that will remain in the QM region and the one that will be eliminated in the MM region. In practice, then, the bonds that are inevitably cut in biomolecules, for instance, are C – C bonds between sp3 carbon atoms. Hydrogen is then a reasonable choice for a capping atom because the electronegativities of H and C are not too different. Nevertheless, a potentially better choice is a pseudo-halogen having seven valence electrons and an electronegativity similar to that of carbon. The ‘lone pairs’ on such a capping atom will then resemble the electrons from the other bonding orbitals that would reside on the atom if the system were fully QM, which may offer a better representation of the system; Zhang, Lee, and Yang (1999) have provided an initial description of a method employing this protocol, using a pseudopotential for the core electrons that provides the appropriate electronegativity behavior.

To date, the use of link atoms has been associated with extra instability in MD simulations at the QM/MM level because of, inter alia, the stiff force constants maintaining linearity of bonds crossing the boundary and the large electrostatic interactions involving atoms near the boundary. Progress in this area, addressing the above and other issues, is expected to continue briskly.

13.3.3Frozen Orbitals

In practice, the source of the greatest instability in the link atom approach is the strong interactions that can develop between the wave function in regions near the link atom and nearby MM atoms carrying partial atomic charges. As noted above, one can attempt to eliminate some of those interactions by fiat, but this tends to lead to other instabilities.

A significant contributor to this problem is the point charge nature of molecular mechanics charges. Smeared-out charge densities are more physically realistic and less prone to computational problems. This suggests that a worthwhile approach would be to have some sort of buffer layer between the polarizable QM region and the point-charge-represented MM region that would be itself represented by a continuous unpolarizable charge density, i.e., one that is not reoptimized as part of an SCF procedure.

While the details are somewhat mathematically tedious, the conceptual basis can be explained relatively simply. The full system is now partitioned into three regions, which may be called the MM region, the auxiliary region, and the QM region. The new auxiliary region is characterized by nuclei having their normal nuclear charges, and electron density expressed in some set of basis functions. Equation (13.1) may now be generalized to yield a Hamiltonian

Compared to Eq. (13.1), there are three new terms, all involving the auxiliary region. However, two of these terms are entirely classical, Haux and Haux/MM. The first is simply the electrostatic interaction of the frozen density and its nuclei with themselves, while the second is the interaction of the frozen density and its nuclei with the MM point charges and non-bonded LJ terms between the two regions.

As for the HQM/aux term, it is in principle not much different than HQM/MM, except that instead of adding one-electron integrals over atomic partial charges to the Fock operator it adds two-electron integrals with the orbitals for one electron being frozen. There is one additional subtle point, and that is that the MOs of the optimized QM wave function must be orthogonal to the MOs describing the frozen density.

Thus far, there have been two reasonably carefully described models implementing the broad philosophy outlined above. However, in reducing the above outlines to practical calculation, certain issues must be considered. First, it would be nice if the frozen density region would remain a constant throughout the course of a simulation (if it has to be recalculated constantly, it is really not much different from the fully QM region). One means to accomplish this is to associate the density with localized orbitals, e.g., spn hybrids on first-row atoms if the system is a protein. In addition, the generation of the frozen density is usually accomplished by a fully QM calculation on the sum of the QM and auxiliary regions, followed by the freezing of the auxiliary portion of the density. As such, the auxiliary region cannot be too large. To date, it has been limited to the atoms at the QM/MM boundary.

The first reported approach along these lines was the localized self-consistent-field (LSCF) method of Ferenczy et al. (1992), originally described for the NDDO level of theory. In this case, the auxiliary region consists of a single frozen orbital on each QM boundary atom,

usually taken to be that atom’s contribution to a localized orbital from a fully QM calculation on a slightly expanded region (that might itself have been capped at some boundary if necessary). The population of the orbital – as fully paired spin density – may either be treated as a free variable, or computed from the density matrix of the original QM calculation. At the NDDO level, once the spatial orientation of the orbital and its s to p ratio have been set, its orthogonality to all other orbitals may be very simply enforced in QM/MM calculations. To maintain an overall zero charge on the QM + auxiliary regions, it is necessary that the total number of electrons in the auxiliary orbitals be equal to the total number of such orbitals, so some care must be taken to ensure excess charge does not introduce problems. The LSCF method, then, looks very much like the link atom method, except that the orbitals describing QM-atom–capping-atom bonds are not optimized as part of the SCF, but are instead treated as frozen throughout. Extension of the LSCF formalism to ab initio HF and DFT levels of QM theory has been described by Philipp and Friesner (1999).

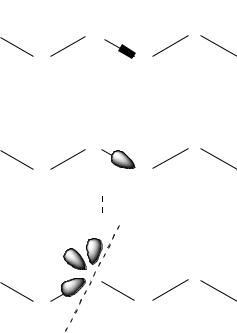
In comparison, a larger auxiliary region is employed in the generalized hybrid orbital (GHO) approach described by Gao et al. (1998). In this case, it is better to think of the QM/MM boundary as passing through an atom instead of through bonds, as certain carbon atoms are assigned both QM and MM character. On those atoms, three sp3 orbitals are held frozen with paired-spin-density populations equal to one minus one-third of the partial atomic charge the atom would carry for MM purposes, i.e., there is an attempt to spread out the character of the boundary atom over its frozen orbitals. The remaining orbital, pointing to the QM region, is frozen in shape by orthogonality constraints, but its population and contribution to the various MOs is free to vary according to the SCF procedure. Thus, there is again a similarity to the link atom procedure, in that there is a fully optimized MO representing each bond at the QM/MM frontier, but in this case the orbital is surrounded by a much more realistic charge environment from the hybrid atom nucleus and its three frozen auxiliary orbitals. The three different approaches are compared schematically in Figure 13.6.

A subtle but key difference in the methodologies is that the orbital containing the two electrons in the C –X bond is frozen in the LSCF method, optimized in the context of an X –H bond in the link atom method, and optimized subject only to the constraint that atom C’s contribution be a particular sp hybrid in the GHO method. In the link atom and LSCF methods, the MM partial charge on atom C interacts with some or all of the quantum system; in the GHO method, it is only used to set the population in the frozen orbitals.

The GHO approach has been designed in such a way that the QM/MM atoms at the boundary are intended to be transferable. Thus, hybrid atoms have modified semiempirical parameters and force-field parameters for use in computing the QM and MM portions of the QM/MM energy according to Eq. (13.4), supplemented by MM bond stretching, angle bending, and torsional terms whenever any one atom in the relevant linkage is a purely MM atom. The modifications have been made for the combination of the AM1 Hamiltonian and the CHARMM force field so as best to reproduce structural, energetic, and charge results from fully AM1 calculations for a spectrum of molecules bearing functional groups similar to those found in proteins. A CHARMM/PM3 implementation has also been reported (GarciaViloca and Gao 2004) as has the formalism for an ab initio Hartree – Fock GHO method (Pu, Gao, and Truhlar 2004).

Figure 13.6 Comparison of QM/MM partitioning schemes across covalent bonds. Included MM bond stretch, angle bend, and torsion terms are indicated; those that are boxed are ignored by some authors. Frozen orbitals are in gray for the LSCF and GHO methods

Analytic derivatives have been reported for both the LSCF and GHO models, making them attractive options for MD simulations (Amara et al. 2000). Their generalization to ab initio levels of theory through the use of core pseudopotentials (along the lines of the pseudohalogen capping atoms described above) ensures that they will see continued development.

13.4 Empirical Valence Bond Methods

A method that has certain connections with QM/MM techniques even if it does not usually involve simultaneous evaluation of QM and MM operators during a particular calculation is the empirical valence bond method (EVB; Warshel and Weiss 1980). At the heart of the EVB method is the notion that arbitrarily complex reactions may be modeled as the influence of a surrounding environment on a fundamental process that may be represented by some combination of valence bond resonance structures. For example, the proton transfer from one water molecule to another may, at any point along the reaction path, be envisaged as involving some admixture of the two VB wave functions corresponding formally to

That is, these two wave functions are taken as the basis functions that are linearly combined to describe the system at an arbitrary point along the proton-transfer coordinate (the proton that is transferred has been labeled with an asterisk and the two oxygen atoms labeled a and b for ease of subsequent discussion).

Most chemists are quite comfortable thinking of chemical structure and reactivity in terms of valence bond notions – the resonance structures so often invoked in organic chemistry are one example of this phenomenon – so this approach has conceptual appeal. From a computational standpoint, the issue is how to derive a Hamiltonian operator that will act on VB wave functions so as to deliver useful energies.

13.4.1Potential Energy Surfaces

VB wave functions like those in Eqs. (13.8) and (13.9) are in some sense MM-like representations of a chemical system. We insist, for instance, that the system described by Eq. (13.8) always has H bound to Oa, irrespective of the length of the bond at any given moment. Obviously, however, if the separation between those two atoms is large, it is absurd to imagine that there is a bond between them. Put more quantum mechanically, one would say that the contribution of that VB basis function to the ‘correct’ adiabatic ground state is very small. Thinking of the adiabatic wave function as a linear combination of the VB basis functions, we would say that the coefficient of 1 in a CI-like expansion should be small, which is equivalent to saying that it must be at rather high energy relative to states making larger contributions.

All of these qualitative considerations suggest that a first step to designing a Hamiltonian for the VB system would be to use a simple force field where the making and breaking O –H bonds are described by a Morse potential, the other OH bonds and bond angles in each of the two molecular fragments are described by harmonic potential functions, and interactions between the two fragments are modeled by standard electrostatic and LJ potential functions. That is, we would have for the uncharged VB Hamiltonian

where the fragments a and b are the molecules containing the oxygen atoms having the same label. Although the bond involving H is unique in using a Morse potential, all MM terms are otherwise standard and assume a defined connectivity consistent with Eq. (13.8).

For the charged VB wave function, we take

where, with the exception of the final term, differences between Eqs. (13.10) and (13.11) simply reflect the differences in O –H connectivity between Eqs. (13.8) and (13.9). The final term, 2, is a parameter that is adjusted to make the relative energies of the two VB wave functions correct at their respective minima. In the current example 2 may be determined as the energy of proton transfer from one water molecule to another in the gas phase (we are still considering only a two-molecule system), which energy is available from mass spectral measurements.

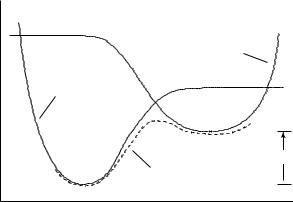
If we were to partially optimize the geometries of the systems having the two possible connectivities, holding fixed only the difference in the two bond lengths from Oa and Ob each to H , we would obtain the set of energy curves for the two VB Hamiltonians shown in Figure 13.7. A crude definition of the energy for the reaction coordinate would then be simply to take the minimum of H1 or H2 as one proceeds from left to right in the proton transfer process. Mathematically, that process is equivalent to taking as our energy the lowest eigenvalue of the 2 × 2 matrix

where H11 is taken to be H1, H22 is taken to be H2, and H12 and H21 are taken to be zero. The matrix then being diagonal, the lowest eigenvalue is simply the lower of H1 or H2.

However, Eq. (13.12) is not simply an odd exercise in matrix algebra. Instead, it suggests a more chemical approach to obtaining the energy of the reacting system. Along the way from the VB structure of Eq. (13.8) to that of Eq. (13.9), the system obviously passes through a region where it is best described as a mixture of these two extreme resonances. The mathematical way in which this mixing can be accomplished is to allow the off-diagonal matrix elements in Eq. (13.12) to be non-zero. The most widely used approximation for these off-diagonal elements in a case like the one discussed thus far is

where A, B, and rOO,‘eq’ are parameters to be optimized against experimental data. Thus, the coupling is designed to decrease exponentially as the two heavy atoms separate from some maximally coupled distance (for more complicated approaches to model H12 see, for example, Chang, Minichino, and Miller 1992 and Kim et al. 2000). With a non-zero coupling, diagonalization of H in Eq. (13.12) will give a curve for the lowest eigenvalue, H0 shown in Figure 13.7, that smoothly connects the two VB extrema. In addition, the eigenvector

matrix elements may be determined in part from QM calculations. However, that could be said of almost any force-field parameter.

A closer relationship between EVB and QM/MM is apparent when some components of the matrix elements are computed ‘on the fly’ at a quantum mechanical level. Mo and Gao (2000), for instance, have described such a technique in the absence of an MM region where an EVB Hamiltonian that includes QM-computed terms is coupled with a surrounding QM region in a non-SCF fashion. The extension of this methodology to include an MM region follows naturally from the QM/MM couplings described above.

It should be apparent that when taken to its QM limit the EVB process simply becomes multi-state CI (see Chapter 14) for a QM system coupled to a classical environment. However, the enormous cost that would be associated with carrying out such a CI calculation at a level sufficiently accurate to compete with an empirically parameterized set of potential functions has inhibited any developments along these lines. Of course, there are interesting systems where data for empirical parameterization are lacking, but the cost of the multi-state CI treatment is still sufficiently expensive that it has not yet attracted any attention.

13.5 Case Study: Catalytic Mechanism of Yeast Enolase

Synopsis of Alhambra et al. (1999) ‘Quantum Mechanical Dynamical Effects in an Enzymecatalyzed Proton Transfer Reaction’.

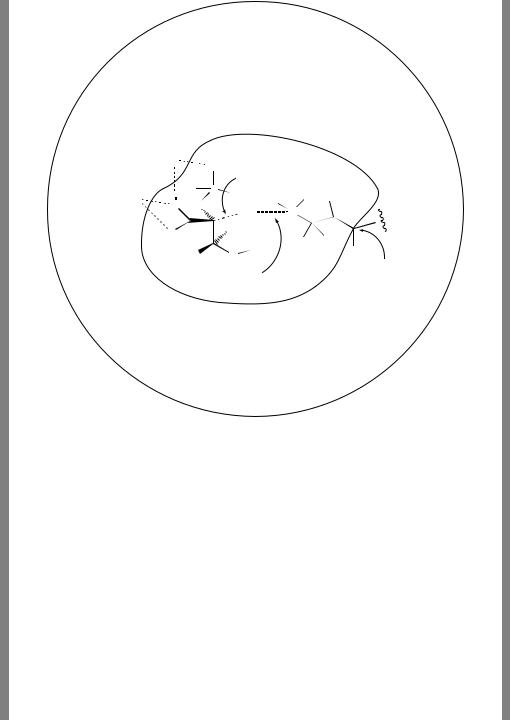
The enzyme enolase catalyzes the dehydration of D-2-phosphoglycerate to phosphoenolpyruvate, a crucial step in the synthesis of carbohydrates for energy storage. A remarkable feature of this reaction is that the rate determining step is removal of a proton from the C-2 position of the reactant that is expected to have a pKa of no less than 32. The base used for this removal is a lysine ε-amino group; additional driving force for the reaction is stabilization of the intermediate tetraanion (the reactant is a trianion) by coordination to two magnesium ions (Figure 13.8).

Alhambra and co-workers adopted a QM/MM strategy to better understand quantum mechanical effects, and particularly the influence of tunneling, on the observed primary kinetic isotope effect of 3.3 in this system (that is, the reaction proceeds 3.3 times more slowly when the hydrogen isotope at C-2 is deuterium instead of protium). In order to carry out their analysis they combined fully classical MD trajectories with QM/MM modeling and analysis using variational transition-state theory. Kinetic isotope effects (KIEs), tunneling, and variational transition state theory are discussed in detail in Chapter 15 – we will not explore these topics in any particular depth in this case study, but will focus primarily on the QM/MM protocol.

The authors’ approach does not actually use a trajectory to investigate the kinetics of the enolase-catalyzed reaction. Rather, the trajectory is designed to create a ‘reasonable’ configuration of the MM part, which is then held frozen as an environment surrounding the QM part, which is subjected to more detailed investigation. Thus, they began from a crystal structure of the enzyme with substrate bound, and propagated a classical trajectory (i.e., no portion was treated via QM) for 50 ps to equilibrate the system. The force field used in this case was CHARMM22. Then, rbreaking and rmaking in Figure 13.8 were held in the region of 1.58 and 1.21 A,˚ respectively, by adding strong harmonic constraints on these bond lengths, and the trajectory was propagated for an additional 10 ps. In principle, this

enolase + water cap

CGHO

rmaking

Figure 13.8 A 25-atom quantum subsystem embedded in an 8863-atom classical system to model the catalytic step in the conversion of D-2-phosphoglycerate to phosphoenolpyruvate by enolase. What factors influence the choice of where to set the boundary between the QM and MM regions? Alhambra and co-workers found, using variational transition-state theory with a frozen MM region that was selected from a classical trajectory so as to make the reaction barrier and thermochemistry reasonable, that the breaking and making bond lengths were 1.75 and 1.12 A,˚ respectively, for H, but 1.57 and 1.26 A,˚ respectively, for D

portion of the trajectory should be representative of the protein structure in the region of the TS for the reaction.

From this 10 ps region, random structures were selected, and QM/MM calculations were carried out at the AM1/CHARMM22 level, with the boundary carbon atom of the lysine side-chain modeled using the GHO approach. In these calculations, the geometry of the MM region was held frozen, but the QM region was optimized to find reactant, product, and transition-state structures. When the computed free energies of activation and of the overall reaction from these structures matched sufficiently closely to experiment, it was assumed that the MM structure was representative of a typical protein configuration in the vicinity of the TS, and a more detailed analysis of the kinetics was undertaken to better understand the experimentally observed isotope effects.