Cramer C.J. Essentials of Computational Chemistry Theories and Models

Ban, F., Rankin, K. N., Gauld, J. W., and Boyd, R. J. 2002. ‘Recent Applications of Density Functional Theory Calculations to Biomolecules’, Theor. Chem. Acc., 108, 1.

Cramer, C. J. 1998. ‘Bergman, Aza-Bergman, and Protonated Aza-Bergman Cyclizations and Intermediate 2,5-Arynes: Chemistry and Challenges to Computation’ J. Am. Chem. Soc., 120, 6261.

Frauenheim, T., Seifert, G., Elstner, M., Hajnal, Z., Jungnickel, G., Porezag, D., Suhai, S., and Scholz, R. 2000. ‘A Self-consistent Charge Density-functional Based Tight-binding Method for Predictive Materials Simulations in Physics, Chemistry and Biology’, Phys. Stat. Sol. B, 217, 41.

Geerlings, P., de Proft, F. and Langenaeker, W. 2003. ‘Conceptual Density Functional Theory’, Chem. Rev., 103, 1793.

Ghosh, A. and Taylor, P. R. 2003. ‘High-level ab initio Calculations on the Energetics of Low-lying Spin States of Biologically Relevant Transition Metal Complexes: A First Progress Report’, Curr. Opin. Chem. Biol., 7, 113.

Jensen, F. 1999. Introduction to Computational Chemistry , Wiley: Chichester.

Koch, W. and Holthausen, M. C. 2001. A Chemist’s Guide to Density Functional Theory, 2nd Edn., Wiley, Chichester.

Laird, B. B., Ross, R. B., and Ziegler, T., Eds., 1996. Chemical Applications of Density-functional Theory , ACS Symposium Series, Volume 629, American Chemical Society: Washington, DC.

Levine, I. N. 2000. Quantum Chemistry , 5th Edn., Prentice Hall: New York.

Perdew, J. P., Kurth, S., Zupan, A., and Blaha, P. 1999. ‘Accurate Density Functional with Correct Formal Properties: A Step Beyond the Generalized Gradient Approximation’, Phys. Rev. Lett., 82, 2544.

Raghavachari, K. 2000. ‘Perspective on “Density Functional Thermochemistry. III. The Role of Exact Exchange”’ Theor. Chem. Acc., 103, 361.

St-Amant, A. 1996. ‘Density Functional Methods in Biomolecular Modeling’ in Reviews in Computational Chemistry , Vol. 1, Lipkowitz, K. B. and Boyd, D. B., Eds., VCH: New York, 217.

Stowasser, R. and Hoffmann, R. 1999. ‘What Do the Kohn-Sham Orbitals and Eigenvalues Mean?’ J. Am. Chem. Soc., 121, 3414.

Worthington, S. E. and Cramer, C. J. 1997. ‘Density Functional Calculations of the Influence of Substitution on Singlet-triplet Gaps in Carbenes and Vinylidenes’ J. Phys. Org. Chem., 10, 755.

Ziegler, T. 1991. ‘Approximate Density Functional Theory as a Practical Tool in Molecular Energetics and Dynamics’ Chem. Rev., 91, 651.

References

Adamo, C. and Barone, V. 1998. J. Chem. Phys., 108, 664.

Adamo, C. and Barone, V. 2002. J. Chem. Phys., 116, 5933.

Adamo, C., Barone, V., Bencini, A., Totti, F., and Ciofini, I. 1999. Inorg. Chem., 38, 1996. Baker, J., Muir, M., and Andzelm, J. 1995. J. Chem. Phys., 102, 2063.

Baker, J., Scheiner, A., and Andzelm, J. 1993. Chem. Phys. Lett., 216, 380. Bally, T. and Sastry, G. N. 1997. J. Phys. Chem. A, 101, 7923.

Bauschlicher, C. W., Jr, and Gutsev, G. L. 2002. Theor. Chem. Acc., 108, 27. Boese, A. D., Martin, J. M. L., and Handy, N. C. 2003. J. Chem. Phys., 119, 3005. Bloch, F. 1929. Z. Physik , 57, 545.

Burke, K., Enzerhof, M., and Perdew, J. P. 1997. Chem. Phys. Lett., 265, 115.

Burke, K., Perdew, J. P., and Wang, Y. 1998. In: Electronic Density Functional Theory. Recent Progress and New Directions , Dobson, J. F., Vignale, G., and Das, M. P., Eds., Plenum Press: New York, 81.

Ceperley, D. M. and Alder, B. J. 1980. Phys. Rev. Lett., 45, 566.

Choi, C. H., Kertesz, M., and Karpfen, A. 1997. J. Chem. Phys., 107, 6712.

302 8 DENSITY FUNCTIONAL THEORY

Chong, D. P., van Lenthe, E., van Gisbergen, S., and Baerends, E. J. 2004. J. Comput. Chem., 25, 1030.

Cohen, A. J. and Tantirungrotechai, Y. 1999. Chem. Phys. Lett., 299, 465. Cramer, C. J. and Barrows, S. E. 1998. J. Org. Chem., 63, 5523.

Cramer, C. J. and Smith, B. A. 1996. J. Phys. Chem., 100, 9664.

Cramer, C. J., Dulles, F. J., and Falvey, D. E. 1994. J. Am. Chem. Soc., 116, 9787. Cramer, C. J., Smith, B. A., and Tolman, W. B. 1996. J. Am. Chem. Soc., 118, 11283. Cullen, J. 2004. J. Comput. Chem., 25, 637.

Curtiss, L. A., Raghavachari, K., Redfern, P. C., and Pople, J. A. 2000. J. Chem. Phys., 112, 7374. Curtiss, L. A., Raghavachari, K., Trucks, G. W., and Pople, J. A. 1991. J. Chem. Phys., 94, 7221. Curtiss, L. A., Redfern, P. C., Raghavachari, K., and Pople, J. A. 1998. J. Chem. Phys., 109, 42. Dirac, P. A. M. 1930. Proc. Camb. Phil. Soc., 26, 376.

Dovesi, R., Orlando, R., Roetti, C., Pisani, C., and Saunders, V. R. 2000. Phys. Stat. Sol. B, 217, 63. Elstner, M., Qui, C., Munih, P., Kaxiras, E., Frauenheim, T., and Karplus, M. 2003. J. Comput. Chem.,

24, 565.

Fermi, E. 1927. Rend. Accad. Lincei., 6, 602.

Filatov, M. and Shaik, S. 1998. Chem. Phys. Lett., 288, 689.

Frenking, G., Antes, I., Bohme,¨ M., Dapprich, S., Ehlers, A. W., Jonas, V., Neuhaus, A., Otto, M., Stegmann, R., Veldkamp, A., and Vyboishchikov, S. F. 1996. In: Reviews in Computational Chemistry , Vol. 8, Lipkowitz, K. B. and Boyd, D. B., Eds., VCH: New York, 63.

Gilbert, T. M. 2004. J. Phys. Chem. A, 108, 2250. Grafenstein,¨ J. and Cremer, D. 2001. Mol. Phys., 99, 981.

Grafenstein,¨ J., Kraka, E., and Cremer, D. 1998. Chem. Phys. Lett., 288 593. Grafenstein,¨ J., Kraka, E., and Cremer, D. 2004. J. Chem. Phys., 120, 524.

Gritsenko, O. V., Ensing, B., Schipper, P. R. T., and Baerends, E. J. 2000. J. Phys. Chem. A, 104, 8558.

Gritsenko, O. V., Schipper, P. R. T., and Baerends. E. J. 1996. Int. J. Quantum Chem., Quantum Chem. Symp., 30, 1375.

Guner, V., Khuong, K. S., Houk, K. N., Chuma, A., and Pulay, P. 2004. J. Phys. Chem. A, 108, 2959. Guner, V., Khuong, K. S., Leach, A. G., Lee, P. S., Bartberger, M. D., and Houk, K. N. 2003. J. Phys.

Chem. A, 107, 11445.

Gunnarsson, O. and Lundqvist, B. I. 1976a. Phys. Rev. B , 13, 4274. Gunnarsson, O. and Lundqvist, B. I. 1976b. Phys. Rev. B , 15, 6006 (erratum).

Hamprecht, F. A., Cohen, A. J., Tozer, D. J., and Handy, N. C. 1998 J. Chem. Phys., 109, 6264. He, Y., Grafenstein,¨ J., Kraka, E., and Cremer, D. 2000. Mol. Phys., 98, 1639.

Hobza, P. and Sponer, J. 1999. Chem. Rev., 99, 3247.

Hoe, W.-M., Cohen, A. J., and Handy, N. C. 2001. Chem. Phys. Lett., 341, 319. Hohenberg, P. and Kohn, W. 1964. Phys. Rev., 136, B864.

Jensen, F. 2002a. J. Chem. Phys., 116, 7372.

Jensen, F. 2002b. J. Chem. Phys., 117, 9234.

Jensen, F. 2003. J. Chem. Phys., 118, 2459.

Johnson, W. T. G. and Cramer, C. J. 2001. Int. J. Quantum Chem., 85, 492. Johnson, B. G., Gill, P. M. W., and Pople, J. A. 1993. J. Chem. Phys., 98, 5612. Jonas, V. and Thiel, W. 1995. J. Chem. Phys., 102, 8474.

Jones, G. A., Paddon-Row, M. N., Sherburn, M. S., and Turner, C. I. 2002. Org. Lett., 4, 3789. Kang, J. K. and Musgrave, C. B. 2001. J. Chem. Phys., 115, 11040.

Khait, Y. G. and Hoffmann, M. R. 2004. J. Chem. Phys., 120, 5005.

Kinnunen, T. and Laasonen, K. 2001. J. Organomet. Chem., 628, 222.

Kohn, W. and Sham, L. J. 1965. Phys. Rev., 140, A1133.

Kormos, B. L. and Cramer, C. J. 2002. J. Phys. Org. Chem., 15, 712. Kummel,¨ S. and Perdew, J. P. 2003. Mol. Phys., 101, 1363.

Lein, M., Dobson, J. F., and Gross, E. K. U. 1999. J. Comput. Chem., 20, 12. Lii, J.-H., Ma, B., and Allinger, N. L. 1999. J. Comput. Chem., 20, 1593.

Lim, M. H., Worthington, S. E., Dulles, F. J., and Cramer, C. J. 1996. In: Density-Functional Methods in Chemistry , ACS Symposium Series, Vol. 629, Laird, B. B., Ross, R. B., and Ziegler, T., Eds., American Chemical Society: Washington, DC, 402.

Liu, H., Elstner, M., Kaxiras, E., Frauenheim, T., Hermans, J., and Yang, W. 2001. Proteins, 44, 484. Lovell, T., McGrady, J. E., Stranger, R., and Macgregor, S. 1996. Inorg. Chem., 35, 3079.

Lynch, B. J. and Truhlar, D. G. 2003a. J. Phys. Chem. A, 107, 3898.

Lynch, B. J. and Truhlar, D. G. 2003b. J. Phys. Chem. A, 107, 8996.

Lynch, B. J., Zhao, Y., and Truhlar, D. G. 2003. J. Phys. Chem. A, 107, 1384.

Ma, B., Schaefer, H. F., III, and Allinger, N. L. 1998. J. Am. Chem. Soc., 120, 3411. Patchkovskii, S. and Ziegler, T. 2002. J. Chem. Phys., 116, 7806.

Perdew, J. P. and Zunger, A. 1981. Phys. Rev. B, 23, 5048.

Perdew, J. P., Burke, K., and Enzerhof, M. 1997. Phys. Rev. Lett., 78, 1396.

Perdew, J. P., Chevary, J. A., Vosko, S. H., Jackson, K. A., Pederson, M. R., Singh, D. J., and Fiolhais, C. 1992. Phys. Rev. B , 46, 6671.

Poater, J., Duran, M., and Sola,` M. 2001. J. Comput. Chem., 22, 1666.

Pokon, E. K., Liptak, M. D., Feldgus, S., and Shields, G. C. 2001. J. Phys. Chem. A, 105, 10483. Poli, R. and Harvey, J. N. 2003. Coord. Chem. Rev., 32, 1.

Proynov, E., Chermette, H., and Salahub, D. R. 2000. J. Chem. Phys., 113, 10013. Redfern, P. C., Blaudeau, J. -P., and Curtiss, L. A. 1997. J. Phys. Chem. A, 101, 8701.

Rienstra-Kiracofe, J. C., Tschumper, G. S., Schaefer, H. F., III, Nandi, S., and Ellison, G. B. 2002.

Chem. Rev., 102, 231.

Ruiz, E., Salahub, D., and Vela, A. 1995. J. Am. Chem. Soc., 117, 1141. Scheiner, A. C., Baker, J., and Andzelm, J. W. 1997. J. Comput. Chem., 18, 775.

Snijders, G. J., Baerends, E. J., and Vernooijs, P. 1982. At. Data Nucl. Data Tables., 26, 483. St-Amant, A., Cornell, W. D., Halgren, T. A., and Kollman, P. A. 1995. J. Comput. Chem., 16, 1483. Staroverov, V. N., Scuseria, G. E., Tao, J. and Perdew, J. P. 2003. J. Chem. Phys., 119, 12129. Thomas, L. H. 1927. Proc. Camb. Phil. Soc., 23, 542.

van Lenthe, E. and Baerends, E. J. 2003. J. Comput. Chem., 24, 1142. Vosko, S. J., Wilk, L., and Nussair, M. 1980. Can. J. Phys., 1980, 1200.

Wiest, O., Montiel, D. C., and Houk, K. N. 1997. J. Phys. Chem. A, 101, 8378.

Woodcock, H. L., Schaefer, H. F., III, and Schreiner, P. R. 2002. J. Phys. Chem. A, 106, 11923. Xu, X. and Goddard, W. A., III. 2004a. Proc. Natl. Acad. Sci (USA), 101, 2673.

Xu, X. and Goddard, W. A., III. 2004b. J. Phys. Chem. A, 108, 2305. Yang, W. and Lee, T.-S. 1995. J. Chem. Phys., 103, 5674.

Zhang, Y. and Wang, W. 1998. J. Chem. Phys., 109, 2604.

Zhao, Y., Pu, J., Lynch, B. J., and Truhlar, D. G. 2004. Phys. Chem. Chem. Phys., 6, 673. Zheng, Y. C. and Almlof,¨ J. Chem. Phys. Lett., 214, 397.

9

Charge Distribution and

Spectroscopic Properties

9.1 Properties Related to Charge Distribution

We know from the fundamental theorems of DFT that the charge distribution (i.e., the density) determines the external potential, and that this determines the Hamiltonian operator, and that this in turn ultimately determines the wave function. So, in a formal sense, one might say that the charge distribution determines all molecular properties. For purposes of presentation, however, we will distinguish between properties that are rather direct measures of the charge distribution, and others, such as rotational and vibrational frequencies, that may be regarded as being decoupled from the charge distribution except to the extent that the molecular potential energy surface is intimately connected with it.

This chapter concerns itself with the prediction of a variety of measurable spectroscopic properties, including molecular multipole moments and polarizabilities, electron spin resonance (ESR) hyperfine coupling constants, nuclear magnetic resonance (NMR) chemical shifts and spin–spin coupling constants, and molecular rotational, vibrational, and photoelectron spectra. Because the modeling of electronic spectroscopy – the prediction of energy separations and transition probabilities between distinct electronic states – is somewhat more complex than these others in implementation, its discussion is deferred until Chapter 14. In addition, some ‘unmeasurable’ properties are examined, the most important of which, because it forms the basis for much chemical reasoning, is the concept of partial atomic charge.

9.1.1Electric Multipole Moments

In Cartesian coordinates, the expectation values of multipole moment operators are computed as

Essentials of Computational Chemistry, 2nd Edition Christopher J. Cramer

2004 John Wiley & Sons, Ltd ISBNs: 0-470-09181-9 (cased); 0-470-09182-7 (pbk)

306 9 CHARGE DISTRIBUTION AND SPECTROSCOPIC PROPERTIES

where the sum of k, l, and m determines the type of moment (0 = monopole, 1 = dipole, 2 = quadrupole, etc.), Zi is the nuclear charge on atom i, and the integration variable r contains the x, y, and z coordinates of all of the electrons j . When is expressed as a single Slater determinant, we may write

atoms electrons

where ψj and rj are the molecular orbital occupied by electron j and its Cartesian coordinate system, respectively. Equation (9.2) is also valid for DFT, where the various ψ are occupied KS orbitals. For ease of notation, we will restrict our discussion to situations where Eq. (9.2) holds, but all of the qualitative details we will consider are equally valid within the more general formalism of Eq. (9.1).

The simplest moment to evaluate is the monopole moment, which has only the component k = l = m = 0, so that the operator becomes 1 and, independent of coordinate system, we have

ij

where N is the total number of electrons (the simplification of the second term on the r.h.s. follows from the normalization of the MOs). The monopole moment is thus the difference between the sum of the nuclear charges and the number of electrons, i.e., it is the molecular charge.

For the dipole moment, there are three possible components: x, y, or z depending on which of k, l, or m is one (with the others set equal to zero). These are written µx , µy , and µz. Experimentally, however, one rarely measures the separate components of the dipole moment, but rather the total magnitude, µ, which can be determined as

µ = µx 2 + µy 2 + µz 2 (9.4)

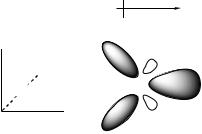
The dipole moment measures the degree to which positive and negative charge are differentially distributed relative to one another, i.e., overall molecular polarity. Thus, for instance, if the electronic wave function has a large amplitude at some positive x value while the nuclear charge is concentrated at some negative x value, inspection of Eq. (9.2) indicates that the dipole moment in the x direction will be negative. If they are both concentrated at the same position and the total electronic charge is equal to the total nuclear charge, the first and second terms on the r.h.s. of Eq. (9.2) cancel, and the dipole moment is zero. Figure 9.1 illustrates the concept for the case of the water molecule. The nuclear charges are shown here lying flat in the xy plane, and entirely at the nuclear positions. The electrons of the

H

y

z

O

x

H

Figure 9.1 Contributions to the dipole moment of the water molecule

hydrogen atoms, however, are pulled to the positive x direction relative to the H nuclei by bonding interactions with the more electronegative O atom (the polarization is exaggerated here by depicting the σ orbitals with surfaces that fail to encompass the nuclear positions). In addition, the oxygen atom contributes two electrons into its in-plane lone pair, the orbital for which is localized at large, positive values of x, while only contributing a single electron each to the σ orbitals, resulting in another net polarization of negative charge in the positive x direction. The sum of these and other effects is such that water has a dipole moment of 1.8 D in the direction indicated (parallel with the x axis by symmetry). Note that the out-of-plane p orbital may be thought of as ‘cancelling’ two protons in the oxygen nucleus when the dipole moment is computed, since it is circularly symmetric about the nucleus when projected into the xy plane. (Since it is also symmetric above and below the xy plane, as are all other orbitals, there is no z component to the dipole moment.)

Note that, if the total number of electrons is equal to the total nuclear charge, then the dipole moment is independent of the choice of origin. This is again fairly obvious from inspection of Eq. (9.2), since any change in origin will affect the total contribution of the first term on the r.h.s. by the same amount as the second term, and the terms have opposite sign; thus, so long as the sum of the atomic numbers is equal to the number of the electrons the net effect of moving the origin is zero. However, if it is not the case that the two are equal, i.e., the system carries a positive or negative charge, then the dipole moment is not independent of origin, since moving it will cause a larger change in the magnitude of the first term on the r.h.s. compared to the second for cations, and of the second term compared to the first for anions. One can show in general that only the first non-zero electric moment of a molecule is independent of origin. For a charged molecule, this is the monopole, for a neutral molecule, the dipole, for a neutral molecule with zero dipole moment (perhaps by symmetry, e.g., CO2), it is the quadrupole, etc. Any other, higher moment that is reported from a calculation must specify the origin that was chosen in order to be meaningful. The most common choices are the center of charge and the center of mass.

Electrical moments are useful because at long distances from a molecule the total electronic distribution can be increasingly well represented as a truncated multipole expansion, and thus molecular interactions can be approximated as multipole –multipole interactions (charge –charge, charge –dipole, dipole –dipole, etc.), which are computationally particularly

simple to evaluate. At short distances, however, the multipole expansion may be very slowly convergent, and the multipole approximation has less utility.

9.1.2 Molecular Electrostatic Potential

A (truncated) multipole expansion is a computationally convenient single-center formalism that allows one to quantitatively compute the degree to which a positive or negative test charge is attracted to or repelled by the molecule that is being represented by the multipole expansion. This quantity, the molecular electrostatic potential (MEP), can be computed exactly for any position r as

Note that this assumes no polarization of the molecule in response to the test charge. The MEP is an observable, although in practice it is rather difficult to design appropriate experiments to measure it. Computationally, it is usually evaluated within the formalism of either HF or DFT theories, in which case one may write

where r and s run over the indices of the AO basis set, P is the one-electron density matrix defined by Eq. (4.57) or its appropriate analog for UHF and DFT, and the orbitals ϕ are those comprising the basis set.

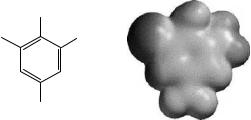
The MEP is particularly useful when visualized on surfaces or in regions of space, since it provides information about local polarity. Typically, after having chosen some sort of region to be visualized, a color-coding convention is chosen to depict the MEP. For instance, the most negative potential is assigned to be red, the most positive potential is assigned to be blue, and the color spectrum is mapped to all other values by linear interpolation. If this is done on the molecular van der Waals surface, one can immediately discern regions of local negative and positive potential, which may be informative for purposes of predicting chemical reactivity. Figure 9.2 provides an example of this procedure for a particular example.

Mapping of the electrostatic potential to grid points in three dimensions has also proven useful for comparative molecular field analysis (CoMFA). This procedure is used to identify common features in the electrostatic potentials of several molecules when the goal is to correlate such commonality with another chemical property, e.g., pharmaceutical activity. In the latter instance, a group of molecules having high activity are oriented about a common origin (finding the correct orientation for each molecule is a key challenge in CoMFA) and the electrostatic potential of each is evaluated at each grid point. A subsequent averaging of the values at every point may identify key regions of positive or negative potential associated

NO2

Figure 9.2 MEP of the radical anion produced by one-electron reduction of the dinitroaromatic shown at left. The spectrum is mapped so that red corresponds to maximum negative charge density and deep blue to minimum (here shown in grayscale). This depiction indicates that the buildup of negative charge density is larger on the nitro group ortho to the amino group than on that para to NH2. Such polarization is consistent with the observed reactivity of the molecule under reducing conditions (Barrows et al. 1996)

with activity and that information may be used for the design of future drug candidates. Full scale CoMFA typically considers more fields than only the electrostatic potential (e.g., steric or non-polar fields), but there is a strong tendency for electrostatic effects to influence pharmaceutical activity and specificity.

For very large molecules (like biopolymers) the ESP can be very useful for analyzing function, but direct calculation from quantum mechanics is restricted to fairly low levels of theory (Khandogin, Hu, and York 2000). An alternative method that shows promise is to assemble the full molecular density from high-level calculations on small constituent fragments (Exner and Mezey 2002).

9.1.3Partial Atomic Charges

A very old concept in chemistry is to associate molecular polarity with charge build-up or depletion on the individual atoms. In rationalizing hydrogen bonding in water, for instance, we speak of the oxygen being ‘negative’ and the hydrogen atoms ‘positive’. Part of the driving force for this conceit is that it allows one to conveniently ignore the wave character of the electrons and deal only with the pleasantly more particulate atoms, these atoms reflecting electronic distribution by the degree to which they carry positive or negative charge. Absolutely critical to the efficiency of most force-field methodologies is that they compute electrical interactions as atom-centered charge –charge interactions, so the development of methods for assigning accurate partial charges to atoms in molecules has seen considerable research.

The concept of a partial atomic charge, however, is ill defined. One often sees it written that the atomic partial charge is not a quantum mechanical observable. This is, however, a bit misleading. One can define unambiguous procedures making use of well-defined quantum mechanical operators for computing the partial atomic charge, and such procedures are in principle subject to experimental realization (e.g., the atoms-in-molecules charges defined in Section 9.1.3.3). However, there is no universally agreed upon ‘best’ procedure

(cf. Eq. (9.7)), and f is a damping factor raised to the nth power. New electronic populations are then computed according to

In the original PEOE method, the damping function f was simply taken to be the constant 0.5, which led to practical convergence in the atomic partial charges within about five iterations. No et al. (1990a, 1990b) subsequently proposed a modification in which different damping factors were used for different bonds (MPEOE) and observed that this, together with some other minor changes, gave improved charge distributions when compared to known multipole moments. More recently, Cho et al. (2001) proposed computing the damping factor as

where rkk is the distance between the two atoms and rvdw is a parametric van der Waals radius. The use of Eq. (9.10) delivers geometry-dependent atomic charge (GDAC) values, which were found to improve additionally on computed electrical moments.

Another Class I charge model that is also sensitive to geometry is the QEq charge equilibration model of Rappe´ and Goddard (1991). From representing the energy u of an isolated atom k as a Taylor expansion in its charge truncated at second order, one can derive

where u˜ is the energy of the neutral isolated atom, χ is the electronegativity (experimentally the average of the atomic IP and EA), and J is the idempotential, which is formally equal to IP − EA. With this formula in hand, we may write the electrostatic energy of a collection of N atoms as

where J is a matrix of Coulomb integrals for which we have already defined the diagonal elements as the idempotentials. The off-diagonal elements are computed as (aa|bb) where a and b are STOs on the centers k and k , respectively (thereby introducing geometry dependence). QEq charges q are then determined from minimization of U subject to the constraint that the total molecular charge remain constant. Note the close conceptual similarities between QEq and SCC-DFTB described in Section 8.4.4.

Eq. (9.12) does not require any specification of bonding – all atoms electrically interact with all other atoms. Sefcik et al. (2002) have combined QEq electrostatics with Morse potentials for non-electrostatic non-bonded interactions between all atom pairs to create a