Cramer C.J. Essentials of Computational Chemistry Theories and Models

atoms, Rienstra-Kiracofe et al. (2002) and Bauschlicher and Gutsev (2002) have separately noted that B3LYP with large basis sets seems to be particularly robust.

Finally, atomic and molecular proton affinities (PAs) have also been evaluated for various functionals for ammonia, water, acetylene, silane, phosphine, silylene, hydrochloric acid, and molecular hydrogen. For G2 and G3 theories, the mean unsigned error in PAs is 1.1 and 1.3 kcal mol−1, respectively. At the SVWN, BLYP, BP86, BPW91, B3LYP, B3P86, and B3PW91 levels (using the 6-311+G(3df,2p) basis set), the corresponding errors are 5.8, 1.8, 1.5, 1.5, 1.3, 1.1, and 1.2 kcal mol−1, respectively (quantitatively similar results have also been obtained with more modern functionals). The much cheaper hybrid DFT methods are thus entirely competitive with G2 and G3, although the data set is perhaps too small to come to any firm conclusions on this topic (cf. Pokon et al. 2001).

8.6.2Geometries

Analytic first derivatives are available for almost all density functionals, and as a result geometry optimization can be carried out with facility. The performance of the various functionals is usually quite good when it comes to predicting minimum energy structures. As summarized in Table 8.5, bond lengths at the LDA level for molecules composed of firstand second-row atoms are typically as good as those predicted from MP2 optimizations, with both these levels being somewhat improved over HF theory. The use of GGA functionals does not usually result in much improvement over the LDA level. However, the GGA functionals tend to systematically overestimate bond lengths. As noted in Section 6.4.2, the HF level tends to systematically under estimate bond lengths. Thus, it should come as no surprise that the hybrid ACM functionals, which mix the two, give noticeable improvement in predicted bond lengths (of course, the improvements are on the order of 0.005 A,˚ and it should be noted that most molecular properties are very little affected by such small variations in bond lengths). Very small improvements in geometrical accuracy are usually noted with increasing basis-set size beyond those listed in Table 8.5. Accuracies in bond angles for all flavors of DFT average about 1◦, the same as is found for HF and MP2. Similarly, the limited amount of data available for dihedral angles suggests that HF, MP2, and DFT all perform equivalently in this area.

Table 8.5 also indicates that the most popular functionals fail to be as accurate for molecules containing third-row main-group elements as they are for molecules made up of elements from the first two rows. The LYP correlation functional seems to perform particularly badly, while the PW91 functional is more robust.

It is, however, for the transition metals themselves that DFT has proven to be a tremendous improvement over HF and post-HF methods, particularly for cases where the metal atom is coordinatively unsaturated. The narrow separation between filled and empty d-block orbitals typically leads to enormous non-dynamical correlation problems with an HF treatment, and DFT is much less prone to analogous problems. Even in cases of a saturated coordination sphere, DFT methods typically significantly outperform HF or MP2. Jonas and Thiel (1995) used the BP86 functional to compute geometries for the neutral hexacarbonyl complexes of Cr, Mo, and W, the pentacarbonyl complexes of Fe, Ru, and Os, and the tetracarbonyl

see Hamprecht et al. (1998).

d A 96-molecule set with the 6-311++G(3df,3pd) basis set, see Staroverov et al. (2003).

complexes of Ni, Pd, and Pt. Over the 10 unique metal–carbon bond lengths for which experimental data are available, they observed no error in excess of 0.01 A˚ except for W, where the error was 0.017 A˚ . At the HF and MP2 levels using equivalent basis sets, the corresponding average absolute errors are 0.086 and 0.028 A,˚ and the maximum deviations are 0.239 and 0.123 A˚ (Frenking et al. 1996).

To the extent DFT shows systematic weaknesses in geometries, it is in those areas where it similarly does poorly for energetics. Thus, van der Waals complexes tend to have interfragment distances that are too large because the dispersion-induced attraction is not properly modeled (although it may accidentally be mimicked by BSSE). Hydrogen bonds are somewhat too short as a rule, and indeed, most charge transfer complexes have their polarities overestimated so that they are too tightly bound. Finally, the tendency noted above in Section 8.5.6 for DFT to overdelocalize structures can show up in geometrical predictions. Thus, for instance, in 1,3-butadiene DFT tends to predict the formal single bond to be a bit too short and the formal double bonds to be somewhat too long (and this extends to other conjugated π systems). As already noted above in Section 8.5.6, this can also lead to a tendency to favor higher symmetry structures over ones of lower symmetry since the former tend to have more highly delocalized frontier orbitals (see also Section 9.1.6). Finally, loose transition state structures can result from this phenomenon; for instance, the C–Cl bond lengths in the TS structure illustrated in Figure 6.12 are 2.45 and 2.39 A˚ at the BLYP/6- 31G(d) and B3LYP/6-31G(d) levels of theory, respectively. Of course, this is a significant improvement over HF theory, and insofar as TS structures tend to be fairly floppy, the remaining geometrical errors may have only small energetic consequences.

Wiest, Montiel, and Houk (1997) have studied carefully a large number of TS structures for organic electrocyclic reactions and, based on comparison to experiment (particularly including kinetic isotope effect studies) and very high levels of electronic structure theory,

concluded that the B3LYP functional is particularly robust for predicting geometries in this area. This is consistent with the good behavior of this functional when applied to minimum-energy structures composed only of first-row atoms as already noted above. Cramer and Barrows (1998) have emphasized, however, that overdelocalization problems can arise in ionic examples of such electrocyclic reactions, and caution may be warranted in these instances.

8.6.3 Charge Distributions

Over the 108 molecules in Test Set B of Table 8.5, Scheiner, Baker, and Andzelm computed the mean unsigned errors in predicted dipole moments to be 0.23, 0.20, 0.23, 0.19, and 0.16 D at the HF, MP2, SVWN, BPW91, and B3PW91 levels of theory, respectively, using the 6-31G(d,p) basis set. These results were improved somewhat for the DFT levels of theory when more complete basis sets were employed.

Cohen and Tantirungrotechai (1999) compared HF, MP2, BLYP, and B3LYP to one another with respect to predicting the dipole moments of some very small molecules using a very large basis set, and their results are summarized in Table 8.6. In general the performances of MP2, the pure BLYP functional, and the hybrid B3LYP functional are about equal, although both DFT functionals do very slightly better than MP2 for several cases. HF theory shows its typical roughly 10–15 percent overestimation of dipole moments, and its historically well-known reversal of moment for carbon monoxide.

In addition to the moments of the charge distribution, molecular polarizabilities have also seen a fair degree of study comparing DFT to conventional MO methods. While data on molecular polarizabilities are less widely available, the consensus appears to be that for this property DFT methods, pure or hybrid, fail to do as well as the MP2 level of theory, with conventional functionals typically showing errors only slightly smaller than those predicted by HF (usually about 1 a.u.), while the MP2 level has errors only 25 percent as large. In certain instances, ACM functionals have been more competitive with MP2, but still not quite as good.

Table 8.6 Dipole moments (D) for eight small molecules at four levels of theory using the very large POL basis seta

a From Cohen and Tantirungrotechai 1999.

(continued overleaf )

(continued overleaf )

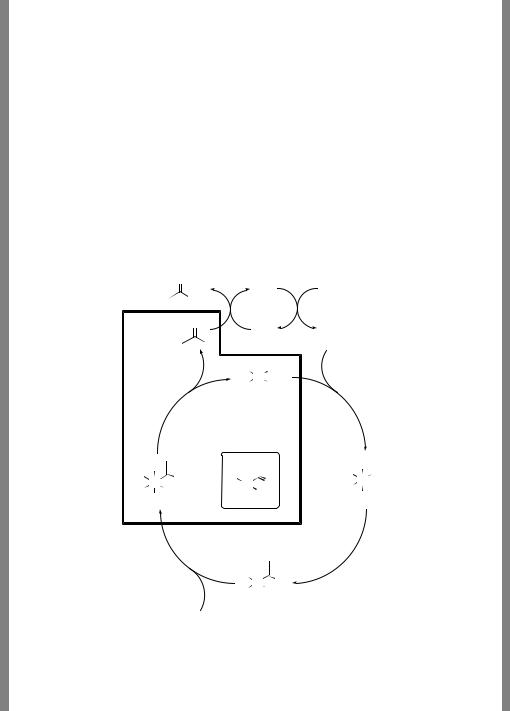
8.7Case Study: Transition-Metal Catalyzed Carbonylation of Methanol

Synopsis of Kinnunen and Laasonen (2001), ‘Reaction Mechanism of the Reductive Elimination in the Catalytic Carbonylation of Methanol. A Density Functional Study’.

Acetic acid is made industrially by the condensation of methanol and carbon monoxide catalyzed by either a diiododicarbonylrhodium species or the corresponding iridium complex. The proposed catalytic cycle for this process is illustrated in Figure 8.5. Experimentally establishing a complete catalytic mechanism can be quite challenging, since reactive intermediates in the cycle may be present at such low concentrations that they are very difficult to detect. Theory can therefore play a useful role in establishing the energetic profiles for proposed catalytic steps, with the ultimate goal being the design of improved catalysts based on a fundamental understanding of the mechanism.

To that end, Kinnunen and Laasonen model the reductive elimination pathways from the anionic acetyltriiododicarbonyl rhodium and iridium anions, and from the acetyldiiodotricarbonyl iridium neutral using the B3LYP functional in combination with an unpolarized

O

OH

O

H2O

MeI

I

ICO

M

ICO

reductive elimination

I

M O

I CO I

CO

Figure 8.5 Catalytic cycle for the metal-catalyzed carbonylation of methanol, with the reductive elimination step highlighted. In the case of iridium, the diiodotricarbonyl species has also been suggested as a possible precursor to reductive elimination. What are the issues of stereochemistry associated with the intermediates? What special basis-set requirements will be involved in modeling this system?