Reactive Intermediate Chemistry

902 REACTIONS ON THE FEMTOSECOND TIME SCALE

with pulsed lasers. But even with the temporal resolutions on the picosecond time scale reached in the 1970s, the time-dependent parameters observable experimentally related to changing populations of reactants and products—to reaction kinetics. Dynamic details remained hidden; the atomic-scale events transpiring at the transition state, or within the transition state region, continued to be objects of speculation, theoretical conjecture, or computation-based modeling. Direct evidence was not accessible.

Reaction dynamics as opposed to reaction kinetics strives to unravel the fundamentals of reactions—just how they transpire, how intramolecular vibrational energy redistributions provide energy to the modes most involved along the reaction coordinate, how specific reaction states progress to specific product states, why product energy distributions and ratios of alternative products are as they are, and, of course, how fast the basic processes on an atomic scale and relevant timeframe occur.

Dynamics deals with the nature of transition regions, treating them today as far more substantial ranges of configurations in time and space than one might infer from a simple, rigid calculated transition structure. The transition state concept enlarged to a transition region perspective is just ‘‘the full family of configurations through which the reacting particles evolve en route from reagents to products’’ at or close to the minimum energy required for the reaction to occur.4

Molecular hydrogen has a vibrational period of only 7.6 fs, while vibrational modes involving heavier atoms are slower. The motions of atoms in activated molecules, the various vibrations and rotations leading to chemical reactions, will generally take place over time periods of 10 to 100 or 1000 fs, the femtosecond time scale. One femtosecond is 10 15 s; ‘‘femton’’ is Swedish for 15, making the femtosecond unit, the next beyond the nicely classical milli-, micro-, nano-, picosecond sequence, easy to remember.

Intramolecular vibrational energy relaxation typically redistributes energy throughout all vibration modes in a molecule in 1 ps, so the observational window for following the contributions of specific vibrations to overall reactions is narrow. One may have significant reaction events taking place much faster than the time required for complete vibrational energy redistribution—a basic presumption of transition state theory. Or a reaction may involve transition regions spacious enough to allow transition structures to exhibit the characteristics of reactive intermediates and persist over times much longer than typical vibrational periods.

To secure detailed descriptions of chemical transformations as they occur within the transition state region based on direct, real-time experimental observations is the ambitious goal of femtochemistry.5 It is chemistry on the femtosecond time scale, the time scale appropriate to the dynamic details responsible for transformations taking place over the transition state region as bond-breaking and bond-mak- ing chemical events evolve. Sometimes the methods used are termed femtosecond transition state spectroscopy (FTS), a descriptor that emphasizes the intent to observe manifestations of chemical transformations in detail as reactants are converted to products over the femtosecond time domain while traversing the transition state region of the potential energy surface.

3. TIME-RESOLVED FEMTOSECOND DYNAMICS

Today, ultrafast pulsed-laser techniques, high-speed computers, and other sophisticated instrumentation make it possible to measure the time evolutions of reactants, intermediates, transition structures, and products following an abrupt photoactivation of a starting material. Detailed theoretical calculations, experienced judgments based on the literature, and newly accessible femtosecond-domain experimental data providing observed intensities of chemical species versus time can provide insights on the atomic-scale events responsible for overall reaction outcomes.

Such experiments depend on a pump–probe–detect strategy.3,6 In a typical femtosecond study, a narrowly defined laser pulse is amplified and split into two components. The pump and probe pulses may each be manipulated by various nonlinear optical interactions and frequency conversion schemes to afford pulses centered at different wavelengths and having defined energies, shapes, durations, and phases. The pump component that excites the sample is typically of higher energy and intensity. The probe component is sent along a variable length path route, then directed along with the pump pulse for delivery to the sample. The probe pulse will arrive at the sample with a small time delay, as defined by the speed of light and a longer path length (Fig. 20.2).

The adjustable optical path length for the probe pulse is defined by a computer controlled translation stage for the time delay desired; given the speed of light, small variations in path length correspond to appropriate changes in the time delay. An optical path increment of 1 mm corresponds to a time delay of 3.3 fs: The translation stage does not have to be adjusted long distances to give suitable pulse delays!

The combined pump and probe beams are focused onto a supersonic beam of reactant in helium within a vacuum chamber containing a time-of-flight mass spectrometer. The pump pulse promotes the reactant to some excited state; the probe

sample + He

Figure 20.2. Schematic outline of typical pump–probe–detect experiments with femtosecond pulses, a molecular beam source, and mass spectrometric detection of transient species. Computer control and data processing instruments, as well as various optical components, are not shown. The time separation t between pump and probe pulses is dictated by the difference in optical path lengths, d, traversed by the two components of the original pulse.

904 REACTIONS ON THE FEMTOSECOND TIME SCALE

pulse, arriving shortly thereafter, ionizes an excited neutral species that is then detected by mass spectrometry. Variations in the pulse delay time and time-dependent ion intensities reveal the rise and fall of excited species and neutral fragments.

The pump and probe pulses employed may be subjected to a variety of nonlinear optical mixing processes; they may be prepared and characterized by intensity, duration, spectral band width, and polarization. They may arrive in the reaction chamber at a desired time difference, or none. The probe pulse may lead to ionizations followed by detections of ions by mass spectrometry, but many alternatives for probing and detection have been used, such as laser-induced fluorescence, photoelectron spectroscopic detection, absorption spectroscopy, and the like.

Another alternative involves focusing the probe pulse onto the silver photocathode of an electron gun, providing a well-defined pulse of electrons through the photoelectric effect so that time-dependent electron diffraction data for shortlived intermediates may be obtained.

4. COHERENCE

The success of femtosecond time-resolved experiments depends on having lasers able to provide sufficiently short and intense pulses, together with an effective integration of all the other instrumentation, optical components, and computers necessary for the enterprise, and on the susceptibility of starting material to photoexcitation. These requirements are readily understood. Success also depends on coherent formation of the excited system through the pump pulse, a consideration not so readily grasped.

For a time there was concern over just how the uncertainty principle would limit what could be achieved with ultrafast laser pulses. The potential problem turned out to be chimerical, not a problem, once coherence came to be appreciated.7–9 This conceptual advance was essential to the successful development of experimental femtosecond chemistry; it did not progress through better lasers and nonlinear optical tricks and faster computers alone.

The concepts and applications of coherent light within the physics and optics literatures were developed vigorously in parallel with advances in lasers and nonlinear optics. They were introduced within the context of molecular systems through nuclear magnetic resonance (NMR) spectroscopy, especially over the past 30 years. The importance of coherence in studies of chemical dynamics came to be appreciated only more recently.7

If the pump pulse is ultrashort, and t E h=2p, where t ¼ st andE ¼ sE, then won’t the uncertainty in E be too large for useful experiments? This anticipation or anxiety turned out not to be the case. A 60-fs width pulse implies an uncertainty in energy, E, of 0.7 kcal/mol, a very large uncertainty when compared with the precision routinely achieved in various spectroscopic measurements—but small in relation to typical bond dissociation energies!

Femtosecond laser pulses are not monochromatic. The pulse duration is very well defined and very short, which means that its frequency in not precisely known,

COHERENCE 905

given the uncertainly principle. A femtosecond laser pulse is a coherent combination over a range of frequency components: the in-phase generation of the components defines the pulse shape, energy, and intensity. It excites a molecule to a number of close-lying energy levels, to give a coherent preparation of a superposition of states having very nearly identical molecular geometrical parameters. The femtosecond laser pulse delivers excitation energy to the molecule under study, sets the time reference for following subsequent chemical events, and, just as importantly, excites many molecular states coherently. The atoms of the excited molecules are initially localized in phase space; all vibrational states formed start to progress toward products in phase.

The energy landscape relevant to a molecular reaction is given by the potential energy surface, a function of electron distributions and nuclear coordinates. The total energy of an isolated molecule is constant and equal to the sum of the potential energy (of the molecule) and the kinetic energy (of the molecule and its constituent atoms). The kinetic energy cannot be negative, so an excited molecule may look for reaction options at energies at or below the energy imparted upon excitation and at or above the potential energy surface.

Ultrafast laser excitation gives excited systems prepared coherently, as a coherent superposition of states. The state wave function (a probability wave) is a coherent sum of matter wave functions for each molecule excited. The exponential terms in the relevant time-dependent equation, the phase factors, define phase relationships between constituent wave functions in the summation.

X

ðr; tÞ ¼ cj jðrÞexpð iEjt=hÞ

j

The matter wave function is formed as a coherent superposition of states or a state ensemble, a ‘‘wave packet.’’ As the phase relationships change the wave packet moves, and spreads, not necessarily in only one direction; the localized launch configuration disperses or propagates with the wave packet. The initially localized wave packets evolve like single-molecule trajectories.

The initial ground-state equilibrium geometry of reactant molecules is largely preserved in the initially formed electronically excited species, with uncertainties at atomic positions much smaller than the range of changes of distances between atoms characteristic of the reaction being followed. This remarkable outcome is encompassed by quantum mechanics and the wave-particle duality of matter recognized by de Broglie (1924) and expressed as l ¼ h=p: the wave length (l) associated with a particle is equal to Planck’s constant (h) divided by the momentum of the particle (p). Coherent laser-pulse excitation ensures that the structural evolution of the excited molecules will follow single molecular trajectories, until the excited molecules and ensemble coherences atrophy through intramolecular or possibly intermolecular perturbations.

When Schro¨dinger introduced matter wave groups or wave packets in 1926 they were strictly theoretical, quantum mechanical formalisms. There were no experimentally accessible ways to prepare matter wave packets from molecules. Now

906 REACTIONS ON THE FEMTOSECOND TIME SCALE

they can be generated with excellent spatial resolution and temporal definition, coherently, over times much shorter than the periods associated with molecular vibrations and rotations. Once created, the matter wave packets evolve over time and reflect chemical dynamics events on the femtosecond time scale.

The photochemical excitation delivered by a narrowly defined pump laser pulse achieves three indispensable things: it sets time ¼ 0, energizes the reactant molecules, and localizes them in space. It induces molecular coherence as excitation of each of the individual molecules involved leads to a coherent superposition of separate wave packets, a highly localized, geometrically well-defined and moving packet—analogous to a classical system, one that can be described using classical concepts of atomic positions and momentum.

5. REPRESENTATIVE FEMTOSECOND DYNAMICS STUDIES

As recently as 15 years ago direct experimental scrutiny of atomic-scale events in the femtosecond time domain was not possible. That long dreamed of goal, to follow in real time the processes involved as molecules are energized and proceed rapidly through transition regions to give reaction products, has now been attained. Exactly what molecules do and how they do it, and how fast they do it on this extremely fast time scale, is a very young but rapidly maturing branch of chemistry: femtochemistry.

The examples gathered here deal primarily with relatively simple organic reactions, though the photodissociation of one inorganic diatomic molecule is included as an historically important paradigmatic process. The examples cover but a fraction of the field, but may serve to illustrate the powers and limitations of the area at its present state of development.

5.1. Sodium Iodide

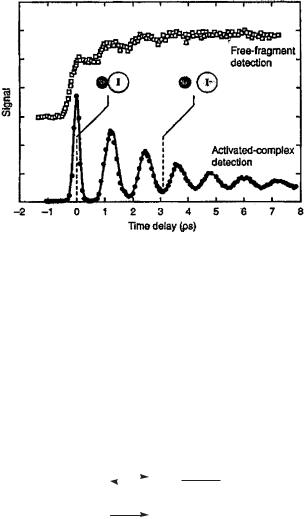
Excitation of NaI to an energy well above the exit channel for formation of Na and I atoms provides a wave packet for bound but highly excited molecules on a steep repulsive potential wall. It moves quickly to a constant energy space and vibrates within the transition state region. The probe pulse induced fluorescence signal indicative of a short, covalent species within the transition state region shows a periodic rise and fall, and an overall damping. The characteristic time for the oscillation depends on the pump pulse wavelenth: When it is centered at 311 nm to is 1.2 ps.10 The oscillation is damped, not exponentially but in steps, for conversion to Na and I atoms occurs most efficiently when the [Na I]z internuclear distance matches the distance at the surface crossing. The signals proportional to covalent [Na I]z

The excited-state potential energy curve for [Na I]z has a covalent inter part and, at longer bond distances, an ionic part, a consequence of a crossing of covalent

Figure 20.3. The time evolution of photoexcited sodium iodide. The signal intensity proportional to covalent ([Na I]z) structures oscillates following the femtosecond pump pulse; the [Na I]z vibrates between covalent and ionic structures before crossing to the lower potential energy surface and dissociating to give Na and I atoms.13 [Reproduced with permission from A. H. Zewail, J. Phys. Chem. A. 2000, 104, 5660.]

and ionic potential energy curves. The oscillation is thus between covalent bonding at short [Na I]z distances and ionic bonding at longer distances. The crossing from the potential heading toward Naþ and I down onto the surface leading to Na and I atoms is rather inefficient. The probability of crossover leading to homolytic dissociation is at a maximum at the shorter [Na I]z bond lengths, and vice versa.

Na—I* crossing Na + I

Monitoring the formation of Na atoms by laser induced fluorescence spectroscopy (at another wavelength) as a function of time shows a stepwise growth in the Na atom intensity, following the implications of the periodic vibration of the [Na I]z species exactly. Thus product formation depends on both a vibrational mode and a curve crossing; both play a role along the reaction coordinate.

This experimental work on the dissociation of excited NaI clearly demonstrated behavior one could describe with the vocabulary and concepts of classical motions.10–13 The incoherent ensemble of molecules just before photoexcitation with a femtosecond laser pump pulse was transformed through the excitation into a coherent superposition of states, a wave packet that evolved as though it represented a single vibrationally activated molecule.

908 REACTIONS ON THE FEMTOSECOND TIME SCALE

5.2. Methyl Iodide

The dissociation of methyl iodide to give an iodine atom and a methyl radical has been studied extensively by a variety of experimental and theoretical techniques. Femtosecond resolved studies augmented the accumulated store of information and insight on this reaction by defining the essential two-dimensional (2D) nature of the reactive vibrational modes leading to products.14,15

Two-photon photoexcitation of CH3I in a molecular beam with a narrow laser pulse at l ¼ 315 nm provides 184 kcal/mol of energy and generates coherent wave packets in two Rydberg states, repulsive states that may lead to C I bond cleavage. The states are well recognized and characterized by spectroscopists; they involve promotions of a 5p p nonbonding electron from iodine to a s* orbital, giving specific 6p or 7s Rydberg states in specific vibronic levels. The signals for the two CH3I* states decayed very quickly, with lifetimes of 166 6 and 131 6 fs. Much longer decays were seen following excitations to the respective excited states of CD3I: the lifetimes were 331 26 and 415 20 fs.

The pronounced isotope effects on excited-state lifetimes imply some involvement of one or more vibration modes in addition to the C I bond distance lengthening along in the reaction coordinate. Quantum molecular dynamics calculations solving the time-dependent Schro¨dinger equation based on a 2D reaction coordinate model, with the CH3 symmetrical stretching along one dimension and the C I bond length along the other, provided a persuasive rationale for the experimental observations. The dissociation takes place initially along the symmetric CH3 vibrational coordinate of the Rydberg states; the wave packets tunnel through a barrier across a seam to access the exit channel leading through elongation of C I to the methyl radical and iodine atom products. The lifetime ratios for CH3I and CD3I Rydberg excited states stem from tunneling and the large differences in reduced mass and zero-point energies of the reactants.

5.3. 1,3-Dibromopropane

A femtosecond time-resolved study of reactions following excitation of 1,3-dibro- mopropane to a (n,5p) Rydberg state uncovered a striking instance of coherent dynamics in a relatively large molecular environment, one characterized by 27 internal degrees of freedom.16,17

The multiphoton ionization mass spectrum of 1,3-dibromopropane shows molecular ions at 200/202/204 amu, thanks to the bromine-79 and bromine-81 isotopes, weak ion intensities for BrCH2CH2CH2 at 121/123, and a base peak at 41,

Figure 20.4. The time evolution of one isotopic version of BrCH2CH2CH2Br* (202 amu) and of the allyl cation (41 amu) formed from the BrCH2CH2CH2 radical upon ionization by the probe pulse. Both intensity versus time profiles show constant periods of 680 fs, with a phase shift of exactly one-half a period.16 [Reproduced with permission from C. Ko¨tting, E. W. G. Diau, J. E. Baldwin, and A. H. Zewail, J. Phys. Chem. A 2001, 105, 1677. Copyright

# 2001 American Chemical Society.]

corresponding to the allyl cation. The 2,2-d2-labeled system gives the corresponding ions at 202/204/206, 123/125, and at both 42 and 43.

The excitation of the unlabeled dibromide followed by a time-delayed probe pulse gives a time-dependent intensity profile for the 202 amu signal. It shows a rapid decay component near time zero (time constant t0) followed by a slower decay (t1). The slower decay exhibits a periodic coherent modulation (tc) and a gradual dephasing (Fig. 20.4).

The two species of 202 amu are taken to be the initially formed Franck–Condon structure and the parent species giving coherent resonance motion; loss of a bromine atom gives BrCH2CH2CH2, which is detected after ionization by the probe pulse as C3H5, at 41 amu. The decay of BrCH2CH2CH2 leads to cyclopropane, a product not ionized by the probe pulse, and hence not seen through mass spectrometry.

Data analysis of the transient signals leads to a deconvolution providing values for the constants t0 ¼ 50 fs, t1 ¼ 2:5 ps, and tc ¼ 680 fs.

The signal for the 41 amu transient, a measure of the time-dependent rise and fall of BrCH2CH2CH2, rises (t1 ¼ 2:5 ps) and then decays (t2 ¼ 7:5 ps), and it shows the same periodic coherent modulation, with a characteristic oscillation time tc ¼ 680 fs, phased shifted by p radians! The local peaks of signal intensity proportionate to the BrCH2CH2CH2 radical concentration match the local troughs of signal decay for the 202 amu periodic modulation; they are 180 out of phase.

910 REACTIONS ON THE FEMTOSECOND TIME SCALE

The most stable ground-state conformation of 1,3-dibromopropane is a C2- symmetric gauche-gauche structure, shown in two perspectives below.

the reciprocal gives the period of the oscillation, 670 fs, a value quite comparable to the observed coherence (tc ¼ 680 fs).

The excited dibromide executes this vibrational mode and the vibrational coherence persists as some trajectories find the C Br bond-cleavage exit channel, a reaction favored when the dihedral angle is close to 60 . The proper phasing of two vibrations, the BrCCC dihedral-angle-modifying torsional mode and the C Br stretching vibration, leads to the cleavage of the C Br bond.

This reading of the situation is supported by parallel studies of BrCH2CD2CH2Br. The fact that time-dependent decays of 42 and 43 amu signals—stand-ins for the BrCH2CD2CH2 radical—both show tc ¼ 7:5 ps, that is, no isotope effect, implies that the decay process does not involve rupture of a C D bond. The loss of HBr or DBr occurs after the monobromo radical is ionized by the probe pulse.

5.4. 1,4-Dehydrobenzene and the Bergman Rearrangement

Photoexciting 1,4-dibromobenzene in a molecular beam with 307-nm pump pulse photons leads to sequential loss of both bromine atoms within 100 fs; the excited dibromide has a lifetime of 50 fs and the monobromide of 80 fs. The p-benzyne generated decays relatively slowly, showing a lifetime of 400 ps.18 It presumably leads to (Z)-3-hexene-1,5-diyne through a valence isomerization of the sort associated with the Bergman rearrangement.

Similar femtosecond observations of the dynamics of 1,2- and 1,3-dehydroben- zene molecules starting from 1,2- and 1,3-dibromobenzene show that each dibromide gives rise to 76 amu intermediates within 100 fs, and that the 76 amu species have lifetimes of 400 fs! Whether o- and m-benzyne intermediates isomerize to p- benzyne and then decay, or just how such isomerizations might occur, remain open to further inquiry.

5.5. 1,4-Cyclohexadiene to Benzene

1,4-Cyclohexadiene may be converted to molecular hydrogen and benzene either thermally or photochemically. The thermal reaction on the ground-state potential energy surface is orbital symmetry ‘‘allowed’’ and is generally considered a concerted pericyclic process. Studies using femtosecond resolved mass spectrometry detected another pathway: A pump pulse excitation of the diene at E ¼ 186 kcal/mol provides an electronically excited state well above the energies required for concerted loss of molecular hydrogen or for loss of a hydrogen atom with formation of a cyclohexadienyl radical.19 The excited starting material of 80 amu decays in 95 10 fs. A transient of 79 amu corresponding to the C6H7 radical is seen: it has a rise time of 50 30 fs and a decay time of 110 30 fs.

A transient at 78 amu is also observed ; since it has the same dynamic characteristics seen for the 79 transient species it may be ascribed to fragmentation of the m=z ¼ 79 cation formed by ionization of the cyclohexadienyl radical induced by the probe pulse.

Careful theoretical analysis indicates a large difference in energy between the concerted pathway and the stepwise, consecutive release of two hydrogen atoms by the excited diene. The concerted elimination may well be strongly favored, and yet the nonconcerted pathway for the elimination to form benzene does contribute. The mechanism for the reaction under the given reaction conditions must include it along with the dominant concerted hydrogen molecular elimination. Further, theoretical assessments of the excited diene at the conical intersection leading rapidly to the ground-state surface suggest that it is highly asymmetrical, and that concerted loss of molecular hydrogen from the ground-state species well above the minimum energy required for the concerted elimination of molecular hydrogen will be controlled by vibrational energy redistribution into the reaction coordinate.

5.6. Norrrish Type-I Cleavages

Photoexcitation of an aliphatic ketone leads to cleavage of a C C bond linking the carbonyl function and an alkyl residue. This a-cleavage process, known as a