
Molecular Heterogeneous Catalysis, Wiley (2006), 352729662X
.pdf416 Chapter 10
and are therefore intrinsically unstable. Carbonium ions decompose into carbenium ions and neutral molecules. The carbenium ions prefer either to back-donate a proton to the zeolite lattice or adsorb as alkoxy species.
Lewis Acidity in Zeolites
Chapter 4
One can distinguish the reactivity of soft cations such as Zn2+ or Ga+ from that of hard cations such as Na+ or Ca2+ through the di erent mix of covalent and electrostatic interactions with these cations. Whereas probe molecules such as CO bind to the hard cations by induced polarization, their binding to soft cations is stronger as it involves additional covalent interaction with d-electrons of the cation. Hard cations can influence the reactivity by creating strong electrostatic fields which stabilize ionic transition states that form as the result of charge-transfer reactions. This is seen in photochemical radical reactions. Soft cations can activate C–H bonds heterolytically or homolytically. Zn2+ , for example, activates alkanes in a heterolytic manner, thus producing a [Zn-alkyl]+ intermediate and a zeolitic proton. Ga+, on the other hand, activates alkanes by oxidative addition, thus forming an [HGa-alkyl]+ intermediate. The adsorbed alkyl intermediate can undergo a subsequent β-C–H scission reaction to form the alkene product.
Pretransition-State Configuration
Chapters 4 and 7
The most stable adsorption state of a reactant molecule on the surface of a catalyst, in the cavity of a zeolite, or within the cleft of an enzyme, typically does not have the appropriate configuration of the reactants necessary to allow them to react directly. Therefore, they typically have to reorient themselves before the reaction can proceed. This requires energy. On a metal surface, this is the energy required to bring fragments close together. This requires overcoming the repulsive lateral interaction energy, especially if they have to share surface metal atoms. In the zeolite cavity, the adsorbed molecules may have to rotate partially to reorient themselves, or else they can first form an intermediate with partially broken hydrogen bonds. In the enzyme, there is reorientation of the reactants to maximize their interaction with peptide functional groups, as well as an adaptation of the framework to optimize the interaction geometry. The small energetic cost of this pretransition-state orientation can have a large e ect on the actual transition-state energies. The transition state are typically lowered substantially as a result of these more favorable reactantcatalyst structures.
Associative Versus Direct Mechanisms
Chapter 4.
The creation of a new bond between two di erent molecules or molecular fragments through consecutive reaction steps is typically called a direct reaction mechanism. In each individual reaction step, a chemical bond between the molecule or molecular fragment and the catalyst surface is formed. The molecular fragments bonded to the catalyst surface can subsequently react with a second adsorbed molecule. In an associative reaction mechanism, a cluster of at least two molecules adsorbs at the reaction center. Bond formation and cleavage reaction, now occur as a single event within the adsorbate cluster consisting of several molecules. This is assisted by transient chemical bond formation with the catalyst surface.
Postscript 417
Di usion in Zeolites
Chapter 4
Di usion in most zeolites cannot be accurately described as Knudsen di usion since the number of collisions between molecules is large compared with that with the micropore wall. Only in the wide-pore zeolite faujasite does the di usion constant show Knudsentype behavior which follows an m−1/2 dependence. In the narrow and medium pore size zeolites, the diameter of the pore is on the order of the diameter of the molecules that we wish to study. The di usion is then dominated by the interactions between molecule and zeolite wall. Once inside the zeolite, the molecules move in the shallow potential of the micropore, hence their rate of di usion becomes mass independent. Di usion inhibition occurs as the result of very narrow pore-size openings. The motion of the zeolite framework atoms controls the di usion barrier.
If molecules can pass one another in the pore, then an increased pore occupation may increase the di usion rates since molecule–molecule interactions may be weaker than molecule–zeolite channel interactions. When molecules cannot pass one another, the phenomenon known as single file di usion may arise. In single file di usion, which tends to occur in one dimensional porous systems, the large reduction in di usion rate is represented by an e ective di usion constant proportional to the center of mass of the file of molecules occluded in the zeolite channel.
When a reaction becomes di usion limited, the product molecules of a zeolite-catalyzed reaction equilibrate. No equilibration, however, can take place between the inner and outer parts of the zeolite. Equilibration within the zeolite occurs with di erent chemical potentials (due to the confined space) than in the gas or liquid phase. The product selectivity in such cases is controlled by inner zeolite equilibration.
Zeolite Medium E ects
Chapter 4
Activation of molecules by protonation depends on zeolite cavity shape and size. Charge separation is screened by the polarization of zeolite lattice oxygen atoms. The stability of intermediate cations strongly depends upon the steric inhibition due to zeolite curvature. The framework of cation-exchanged zeolites behaves as a Lewis base. Heterolytic reactions are promoted in which a proton is accepted by the basic zeolite framework.
Structure Dependence of Zeolite Reactivity
Chapter 4
The dominant interactions between the zeolite framework and the hydrocarbon are van der Waals dispersion interactions that take place between the polarizable zeolite oxygen atoms and the adsorbed hydrocarbon. These interactins are in addition to those between the hydrocarbon and the protons or cations which lead to the activation of the hydrocarbon. The overall van der Waals interaction between hydrocarbon and zeolite cavity depends strongly on the match of hydrocarbon size and shape and that of the zeolite cavity. As a consequence, at the same partial pressure and temperature, the micropore occupation of di erent zeolites may vary significantly for the same adsorbents. This has an important consequence on zeolite catalysis that depends on the concentration of reactant molecules adsorbed at reaction centers. Second, it will strongly a ect the rates of di usion which are strongly micropore occupation dependent.
418 Chapter 10
Oxygen-atom Reactivity
Chapters 4 and 5
In oxides such as V2O5 or MoO3, the M=O bond, which has a bond order of three, is strong, and can help to abstract hydrogen atoms from the reactants. The M=O bond, however, is too strong to be able to insert its oxygen atom into the reactant substrate. In contrast, cation-bridging oxygen atoms are readily inserted into hydrocarbon reactants. The bridging oxygen atom is more weakly bonded with a lower bond order. In addition, energy is gained because of oxide reconstruction upon the oxygen transfer. This can take on various forms. Locally, the octahedrally coordinated cations can be converted into tetrahedrally coordinated cations. In some instances there are more dramatic changes such as those which occur as a result of glide shear planes.
In addition, the bridging oxygen atoms of cationic clusters are highly reactive. In zeolites, the protonation energy of the oxygen atom bridging a cationic cluster occluded in the zeolite is higher than the protonation energy of the basic zeolite-lattice oxygen atoms. Oxygen atoms coordinated to cations of high valency are highly electrophilic and reactive (e.g. [AgO]+). Oxygen atoms bonded to atoms in low-valency states are usually less reactive (e.g. AgOAg).
Proton Transfer Mechanism
Chapters 4 and 6
Since H2O will readily form a hydronium H3O+ in the presence of a proton, the coadsorption of H2O near a reaction complex in which heterolytic bond splitting occurs with generation of a proton can significantly lower the activation energy of such a reaction.
Instead of direct proton transfer to a basic Lewis oxygen atom, coadsorbed H2O will more readily accept the proton and then transfer one of its other hydrogen atoms as a proton to the accepting oxygen atom. This two-step path can also be carried out simultaneously ,thus leading to more direct hydrogen shuttling path.
Hybridization at Transition-Metal Oxide/Sulfur Surface
Chapter 5
In transition-metal compounds such as metal oxides and metal sulfides, the chemical bonding of a transition-metal cation can be rationalized using concepts derived from organometallic chemistry such as atomic hybridization. A cation in a bulk metal compound which is surrounded octahedrally by six anions can be described by six hybridized d2sp3 oriented orbitals. A cation which is tetrahedrally coordinated is described by four sp3 orbitals whereas that which is in a planar configuration is described by four sp2 d- hybridized orbitals. An approximate electronic structure diagram for the oxide can be constructed by considering that each oxygen atom contributes two electrons in an s-type atomic orbital. In an oxide, six bonding and six antibonding orbitals are then formed between an oxygen and a d2sp3-hybridized cation. When the hybridization is sp2 d or sp3, four bonding and four antibonding orbitals are formed, respectively. The bonding orbitals can be considered doubly occupied. Then the d-orbitals are occupied with as many electrons as required for charge balance. In octahedral symmetry, three nonbonding d-orbitals are available. In tetrahedral and planar coordination, five and four d-orbitals, respectively, are available. At the surface, an oxygen anion vacancy creates an empty lone pair orbital which is directed towards the vacancy. On the surface oxygen atoms, occupied lone pair orbitals are formed. This creates surface Lewis acid and base sites.
Postscript 419
Pauling Charge Excess
Chapter 5
Within the ionic chemical-bonding description, the bond order of a chemical bond is determined by the cation or anion charge divided by the number of nearest-neighbor atoms. In a stable system, the sum of the bond orders of the bonds from the coordinating counter ions should not di er by more than ±16 from the cation or anion charge. This is the Pauling stability criterion. At a surface, the charge excess is much larger. A high positive charge excess implies Brønsted or Lewis acidity and a large negative charge excess implies Brønsted or Lewis basicity.
Synchronized Action
Chapter 7
Pretransition-state stabilization in enzyme catalysis occurs by a synchronized adjustment of multiple atom positions in the enzyme. The resulting multipoint adsorption of the reactant maximizes its interaction with the activating enzyme atoms or substituents. It also results in an overall entropy loss. This loss becomes larger as the fit between the reactant and the cavity created by the enzyme becomes tighter. Hence, pretransition stabilization occurs only with an optimum motion of the enzyme atoms so that the free energy is maximized
Influence of Aqueous Media
Chapter 6
Solvents can play an active role in promoting the reaction chemistry for a wide range of di erent reactions carried out in solution. Similar e ects can also be found in surfacecatalyzed reactions. In particular, protic solvents such as water help to stabilize the heterolytic dissociation of molecules into solution by stabilizing the charge on the anion and the cation that form. Water is both a H+ acceptor and an OH− donor. Water can act in a classical way to help stabilize the transition state of charged complexes over the uncharged reactant states in catalyzing a solution-phase reaction. More interestingly, water can actually take part in the chemistry by o ering a conduit to conduct protons.
For reactions that occur over a surface carried out in a protic solvent, both homolytic and heterolytic bond activation steps are possible. Which route prevails depends upon various factors, which include the ability for the anion and the proton that form to migrate into solution, while thermodynamics would suggest that both the anion and the proton prefer to reside in the solution phase. This, however, is di cult to accomplish since an anion that forms has a relatively strong interaction via charge transfer from the anion into unfilled states of the metal. In addition, because of its size, the anion would also pay a high energy penalty for desorption into solution because of the cost associated with solvent reorganization. The protons, on the other hand, typically do not bond very strongly to a neutral surface. In addition, they are much more mobile than the anions and can therefore more readily shuttle o into solution.
A second alternative for the heterolytic activation path involves anion adsorption and proton dissolution. This results in the well-known double layer seen electrochemically. In order for this heterolytic path to proceed, the surface must be able to accommodate the extra electron and therefore the work function of the metal must be higher than 4.8 eV. The water here facilitates proton transfer.
420 Chapter 10
Electrocatalysis
Chapter 6
The potential that results at an electrochemical interface can significantly influence the reactivity of the electrode surface. More negative potentials are more reducing whereas more positive potentials are more oxidizing. The influence of the potential can be accounted for by simply calculating the overall surface energies for homolytic reactions and then shifting the energies by the potential required to match the standard hydrogen electrode. A more rigorous analysis of the influence of the electrochemical potential, however, indicates that the applied potential can significantly polarize the surface in the presence of solution and thus lead to more enhanced changes in the chemical bonding to the surface as well as surface reactivity.
The reactions for C–H, O–H and S–H bond activation typically involve metal atom insertion reactions. In the presence of solution, the hydrogen that forms can be directly transferred into solution as proton. The site dependence for these reactions, which are at the heart of many electrochemical processes, may not be very strong. The reactivity of terraces, steps and kinks may be quite similar. This is di erent to the activation of the molecules over a metal in the gas phase, which is structure sensitive. The electrochemical behavior will, of course, be strongly dependent upon the potential.
An alcohol or acid can adsorb at an electrode as an alkoxide or a carboxylate anion respectively, whereas the proton is accepted by H2O. One can consider this as H2O assisted chemisorption. On the other hand, if H2O dissociation is rate limiting, as is the case for oxidizing conditions, OH surface species are found. The reactivity will then strongly depend on the presence of steps or kinks.
Innerand Outer-Sphere Reactions
Chapter 6
Coordination complexes in a solvent tend to have two reaction modes:
–Inner-sphere reactions:
Chemical reaction occurs between molecules or ions, coordinated to the central metal atom, that are in the first coordination shell of the complex. Reacting molecules are
in direct contact with the cationic center. Bond formation or cleavage can occur by direct (non-cation intermediated) reactions between ligands (such as H+ transfer) or are activated by the redox center.
–Outer-sphere reactions:
Reactions occur by the interaction of a molecule or in the solvent with a molecule ion that is a ligand of the coordination complex.
Evolutionary Adaptive Synthesis Processes
Chapter 8
The molecular recognition of a template by a self assembling system leads to preferential assembly of a unique synthesis reaction intermediate. Through nucleation processes, the intermediate undergoes self assembly with other intermediates and results in the formation of cavities or channels in a substance uniquely related to the template. When the template resembles a particular transition state, the material may have unique selectivity with respect to the corresponding reaction.
Postscript 421
Self Assembly
Chapter 8
Self assembly involves the organization of molecules in a cluster or ordered system. The structure of the self assembled state is ordered and molecules interact through weak hydrophobic or hydrophilic interactions. Structural aspects are often important. Self assembly is a process that is driven by thermodynamics. The final state is a local or absolute minimum free energy state.
Self Organization
Chapter 8
Stationary oscillating states arise far from equilibrium when autocatalytic elementary reaction steps are part of the catalytic cycle. Synchronizing the phase of catalytic reaction cycles in di erent parts of the catalyst is assisted by delaying events such as self organization. Overall reaction rates may show temporally varying phenomena such as oscillations or chaotic time dependence. On the surface of the catalyst, patterns in the form of spirals or replicating pulsars can occur. It is a property of so-called complex systems, in which the components interact in a specific way. Excitable systems are built from autocatalytic reactions that amplify signals and contain an inhibition reaction. When activated beyond a particular threshold, the system may show complicated time-dependent behavior. When the components have di erent di usion rates, the system can self organize in complicated patterns that may show replicating features.
Self Repair
Chapter 8
In addition to the changes in the chemical bonds of the adsorbates that occur during a catalytic cycle, there are also changes in the chemical bonds of the catalyst that take place. Some bonds are weakened whereas others are broken. These bonds must be restored upon completing the catalytic cycle in order for the cycle to continue. This catalytic process then is one which must contain self repair.
The Complexity of the Catalytically Reactive Phase
Chapters 2, 3 and 8
Whereas defects such as kinks or steps are often sites of unique reactivity, the reactive phase of a heterogeneous catalyst is often locally disordered and transient in character. In self organizing systems, these local events can be ordered in time and space. During the course of the catalytic cycle, adsorbed molecules are converted into fragments and subsequently transferred into product molecules which ultimately desorb. In addition to these molecular rearrangements and transformations, the atoms on the surface of the catalyst can also become displaced as a result of local and long-range reconstruction processes. Di usion, adsorption, desorption, dissociation and recombination reactions can all occur with quite di erent demands on the local arrangement of atoms about the reactive center where a specific reaction occurs and its environment.
422 Chapter 10
Templated Catalyst Synthesis
Chapters 8 and 9
Organic cations are able to complex silicate anions to form silicate complexes. These complexes can condense to form ultimately microporous zeolite structures. Di erent templating molecules may form di erent microcavities. Hence zeolite synthesis is an example of template-directed synthesis. Mesoporous materials can be prepared by using nanometersized micelles preorganized as liquid crystals as a template rather than a single molecule template.
Artificial Catalytic Chemistry
Chapter 9
Computational models that use cellular automata to simulate the reproduction of primitive cells, are often composed of:
–A metabolic system of autocatlytic molecules
–Self replicating molecules that inherit genetic information
–A self organizing membrane molecule to close the system.
Such models can be developed for the computational design of catalytic systems that self organize and adapt themselves for optimum catalytic performance. Adaptation occurs in the reproduction process with mutation of the self-replicating molecules coupled to the metabolic system. The metabolic system acts as the bio-immune molecular recognition and response system. The conditions for the emergence of such a system are far from equilibrium in the complex regime. The behavior as a function of time is unpredictable, similar to the class 4 system proposed by Wolfram.
Biomineralization
Chapter 9
Biomineralizatoin involves the exploitation of liquid crystal or self ordering properties of amphiphilic molecules or polymers to design inorganic materials with porous structures ordered over several dimensional length scales.
Aggregation Kinetics
Chapter 9
The non-template-controlled synthesis of amorphous porous materials occurs through aggregation processes in which the relative rate of chemical bond formation and rate of component di usion compete. The aggregates initially formed often have fractal properties that depend on the ratio of these two parameters. Ultimate pore formation occurs via a secondary aging process in which the walls densify.
APPENDICES
Computational Methods
Introduction
A comprehensive understanding of the electronic, molecular, microand meso-scale issues associated with modeling catalytic processes requires a multiscale approach in order to integrate:
1.the electronic and structural changes that govern the intrinsic reaction steps
2.the dynamics of adsorbates in the adlayer and the atoms in the catalytic surface
3.the kinetics for the physicochemical adsorption, reaction and di usion processes
4.the fluid dynamics along with heat and mass transfer in the reactor
5.the deactivation to the catalyst over time.
This would cover changes in time-scale which range from 10−15 sec for electronic transitions to months and years for deactivation phenomena. In addition, this spans a range of length scales that cover ˚angstroms to meters. These same multiscale issues are apparent in a number of other engineering systems where chemistry is important. Multiscale modeling has, therefore, been a subject of much interest. Our focus in this book is predominantly on the intrinsic physical chemistry and the operative catalytic kinetics. This limits the scope to understanding structure and dynamics of the electronic, atomistic and microscopic scales. This requires the integration of electronic structure methods to establish the catalytic reaction steps and the influence of the local environment, along with atomistic methods in order to simulate kinetics, dynamics and equilibrium.
In the three Appendices A–C, we provide a broad overview of electronic structure, atomistic, and kinetic simulation methods along with references for readers who are interested in more detailed discussions. In general, electronic structure methods are used to solve the Schr¨odinger equation subject to a series of fundamental approximations. Schr¨odinger’s equation describes the state of the many body N -electron system and its corresponding energy. The solution thus provides information on the electron states in the system, along with the population of these states with electrons. Schr¨odinger’s equation can ultimately be used to calculate a wide range of di erent properties that are based on the electronic structure of the system including relative energies, geometric structure, spectroscopic signatures, and reactivity. The fundamental entity in electronic structure methods is the electron and is based on quantum mechanics. The system is described by the fundamental forces that act upon the electron. Quantum mechanical methods can typically be characterized as either semiempirical or ab initio. In general, ab initio methods can be subdivided into wavefunction methods and density functional theory. Quantum mechanical methods are necessary for modeling electron transfer processes or chemical reaction steps since they require modeling of the changes that occur to electronic structure. Electronic structure calculations, however, are only practical for systems which have fewer than 103 atoms for the highest level computing systems or a few hundred atoms on more conventional computing systems.
The fundamental entity in atomistic or molecular simulations is the atom or the molecule and is based on the fundamentals of statistical mechanics. The detailed electronic structure is no longer present, thus preventing the treatment of electron transfer, bond breaking and bond making processes. The system is instead described by the forces that act upon the atoms or molecule. This significantly lowers the CPU cost on a per atom basis, thus allowing the simulation of 106–107 atoms. Atomistic simulation can be
Molecular Heterogeneous Catalysis. Rutger Anthony van Santen and Matthew Neurock
Copyright © 2006 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim
ISBN: 3-527-29662-X
424 Appendices
divided into methods for simulating equilibrium properties including structure, sorption and phase behavior, dynamic properties such as di usivity and thermal conductivity, and kinetic properties such as reactivity.
A: ELECTRONIC STRUCTURE METHODS 1. General overview
The goal of quantum mechanical methods is to predict the structure, energy and properties for an N -particle system, where N refers to both the electrons and the nuclei. The energy of the system is a direct function of the exact position of all of the atoms and the forces that act upon the electrons and the nuclei of each atom. In order to calculate the electronic states of the system and their energy levels, quantum mechanical methods attempt to solve Schr¨odinger’s equation. While most of the work that is relevant to catalysis deals with the solution of the time-independent Schr¨odinger equation, more recent advances in the development of time-dependent density functional theory will be discussed owing to its relevance to excited-state predictions.
The following discussion on electronic structure methods is rather general in order to provide a simple overview. More in-depth discussions can be found in a number of very good references, including [1–11].
The time-independent Schr¨odinger equation is |
|
ˆ |
(A1) |
HΨ = EΨ |
where Ψ is the wavefunction and is the energy of the -particle system. ˆ is the
E N H
Hamiltonian operator, which is comprised of the kinetic and potential energy operators which act on the overall system wavefunction Ψ. The wavefunction can extend between +∞ and −∞ and depends upon the positions of the atoms in the system along with the spin of each electron. The square of the wavefunction (Ψ2) describes the probability distribution for the N -particle system. The Schr¨odinger equation is actually nothing more than a force balance on the electrons and the nuclei of the system. The Hamiltonian is
comprised of two essential terms, the kinetic energy operator, ˆ, and the potential energy
T
operator, ˆ . For an -particle system, these operators can be written as
V N
N |
N |
2m1 |
i2 |
N |
2mi |
∂x2 |
+ ∂y2 |
+ ∂z2 |
|
(A2) |
|||
Tˆ = − i=1 |
Ti = − =1 |
= − i=1 |
|||||||||||
|
i |
h¯ |
|
|
h¯ |
|
∂2 |
|
∂2 |
|
∂2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
NN
ˆ |
i |
|
(A3) |
V = |
|
Vij |
=1 j>i
where Ti is the kinetic energy of particle i and Vi and Vj refer to the potential energy terms for electronic interactions between electron–electron, electron–nuclei and, nuclei– nuclei interactions.
A number of simplifying approximations are required to solve this N -particle system, as will be discussed later. The first is the Born–Oppenheimer approximation, which indicates that since the mass of an electron is nearly 2000 times smaller than the mass of a proton, the electrons move many orders of magnitude faster than nuclear motion. Therefore, the electronic motion can be strictly decoupled from the nuclear motion. The electronic
Computational Methods 425
wavefunction can then be solved separately for a fixed set of nuclear positions (R). The hamiltonian for the electronic system now becomes
ˆ |
n |
h¯ |
|
n |
N |
|
|
Za |
|
|
n |
n |
|
|
1 |
|
|
|
|
i |
2 |
i |
|
|
|
|
2 |
i |
|
|
|
|
|
2 |
|||||
H = − |
2mi |
i − |
| |
ri |
− |
Ra |
| |
e + |
| |
ri |
− |
rj |
| |
e |
|||||
|
|
a |
|
|
|
|
j>i |
|
|
|
|||||||||
Kinetic Nuclear–Electron Attraction Electron–Electron Repulsion
n |
n |
ZaZb |
|
|
||
|
|
|
||||
| |
− | |
|
|
|||
+ |
|
Ra |
Rb |
|
e2 |
(A4) |
a |
b>a |
|
|
|||
Nuclear–Nuclear Repulsion
The first term of the hamiltonian describes the kinetic energy of the electron. The second term describes the attractive interaction between the electron and the nuclei where ri and Ra refer to the positions of electron i and atom a. The number of electrons is defined as n and the number of nuclei as N . The third term describes electron–electron repulsion. The final term refers to the nuclear–nuclear repulsive interactions. Since the nuclear charges are decoupled from the electronic wavefunction, this summation can be computed in a straight forward manner and does not change upon the solution to the electronic structure.
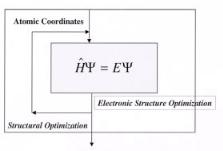
The Born–Oppenheimer approximation[1] is usually a very good approximation since the nuclear mass is so much greater than the electronmass[2,3] . Uncoupling the electronic motion from the nuclear motion enables one to solve for the electronic structure for a fixed set of nuclei. The final term, which describes electron–electron repulsion, prevents the direct solution to the electronic structure. The solution requires convergence of the electronic structure via an iterative scheme. This is known as the self-consistent field approximation, which is discussed later[3,4].
Figure A1. The lowest level hierarchical structure for most quantum mechanical computational algorithms. The inner loop is used to converge the self-consistent field in order to establish the electronic structure to within a user-defined tolerance. The outer loop is used to optimize the structure to within a defined geometric tolerance.
Nearly all quantum mechanical codes are comprised of the basic structure shown in Fig. A1, where there are two primary nested loops. The inner loop requires the convergence of the electronic structure for a fixed set of atomic positions. The outer loop moves the
