
Molecular Heterogeneous Catalysis, Wiley (2006), 352729662X
.pdf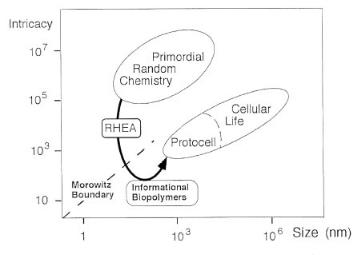
376 Chapter 9
Figure 9.3. A compositional space diagram illustrating conjectural rough relationships between assembly composition and size in early prebiotic events. Intricacy, the number of di erent types of molecular species in an assembly, is plotted against assembly size. Early prebiotic chemistry is assumed to have generated many millions of di erent organic molecules in the size range of a few hundred daltons. These may have formed small assemblies (e.g. micelles) in the 0.1–10 µm range. Such primordial assemblies might lie in a region of the diagram (upper oval) where intricacy is related to assembly size as dictated by a multinomial distribution statistics. A hypothetical path is shown (thick arrow) from prebiotic random chemistry to more biased, life-like assemblies, capable of transmitting compositional information. It is proposed that mutual catalysis-based, “metabolisms first scenarios”, provide a likely path for such assemblies to cross the Morowitz boundary (broken line, representing a probability = 0.5 for successful division), by selecting subsets of molecules. Below this boundary, those assemblies that grow and split can propagate their compositional information with some fidelity. This consequent decreased intricacy, potentially associated with only minor changes of assembly size, means the generation of assemblies with a relatively small number of types of low molecular weight chemical species (“monomers”), thus paving the way for informational biopolymers. Only then may intricacy rise again, as the complex attributes leading to cellular life begin to emerge. Protocells may have been characterized by an augmented size, and the appearance of structural complexity, with only modest increase of intricacy. This trend is clearly manifested in present day cells, which may be up to 1 mm in size, contain trillions of molecules, but may
have only a few tens of thousands di erent kinds of molecular species, including proteins. Adapted from D. Segr´ and D. Lancet[23b].
reach homeostasis. This implies replication with continued growth. The latter is ensured by autocatalytic events. In the two-dimensional Lattice Artificial Chemistry approach proposed by Ono[24a] and Ikegami[24b], the emergence of protocells is actually followed by the reproduction of cells. Selective growth occurs of those cells that have the higher activity of membrane production. Chemicals are represented by particles on reaction sites arranged at a two-dimensional triangular lattice. Chemical reactions are expressed by the probabilistic transition between di erent particle types. There are five types of particles: A, M, X, Y, and W. A particle A replicates itself by consuming a resource particle X using it self as template:
X + Atemplate + Acatalyst −→ 2Atemplate + Acatalyst
It can also catalyze the production of membrane particle M by consuming resource particle X. All particles can decay into waste particles Y, which are recycled into X by an external

Heterogeneous catalysis the origin of life, biomineralization |
377 |
Figure 9.4. Reaction paths. Particle A produce A or M from X. All particles decay into Y. There is a source which supplies X.
source. The number of particles is, hence, constant. Particles W play the role of water. Particles A and W are hydrophilic, particle M is amphiphylic and particles X and Y have neutral interactions. The reaction is represented schematically in Fig. 9.4. As in conventional lattice Monte Carlo methods, di usion is expressed by random walks of particles on the sites. Autocatalytic and membrane particles are assumed to be larger molecules so that their di usion coe cients are smaller than those of other particles.
Ono and Ikegami found that the evolution of the system is roughly divided into three characteristic stages:
1.chemical evolution;
2.emergence of protocells;
3.cellular evolution.
Figure 9.5a. Chemical evolution. The white regions are dominated by particle M. The depth of gray
shade represents the total population of the autocatalysts ( Ai). The black regions are dominated by particle W. Resource and waste particles are not displayed. Pieces of membranes are produced by the catalysts which emerged through mutations[24a].
In chemical evolution small pieces of membrane are formed. Once membranes are formed, there is a restriction in the di usion of molecules. A di erence in concentration or di erent sites within the membrane emerges (Fig. 9.5a).
Most regions become inactive, while there remain some active regions in which protocells help reproduction. The autocatalysts inside them reproduce themselves and me-

378 Chapter 9
Figure 9.5b. Emergence of protocell structures. As the membranes grow, the competition for resources between regions separated by membranes takes place. The regions di erentiate into two states. In some regions that are enclosed by membranes, the density of autocatalysts stays high. In the other regions, their density becomes almost zero[24a].
Figure 9.5c. Reproduction of protocell. Snapshots from 300,000 iterations to 327,000 iterations. The protocell indicated by the white arrow grows gradually in size. When it becomes too large, another membrane appears inside it. Finally, it divides the cell into daughter cells. On the other hand, the cell indicated by the gray arrows could not produce enough membrane particles to keep its membrane. Catalysts in the cell di use away through the defect of the membrane[24a].
Heterogeneous catalysis the origin of life, biomineralization |
379 |
tabolize the membrane particles to maintain their membranes. These assemblies are the protocells (Fig. 9.5b).
When a protocell grows inside, it starts to produce more membrane particles than it needs to maintain its membrane. When it reaches a particular size, surplus membrane particles begin to form another membrane within the cell. This divides the mother cell into a few daughter cells (Fig. 9.5c). A Darwinian selection principle appears to operate. Owing to cellular selection the population of catalysts is biased towards higher membrane production activity.
The model, as presented, can be changed into an artificial catalytic cell by introducing the selection principle that only particular waste molecules are desirable products and other cause cell death, by poisoning (membrane) catalytic sites. The cell can, in principle, be trained to produce the desired molecules as waste. For instance, shape-selective di usion can be incorporated for molecules moving through the cell membrane, allowing desired molecules of particular shape to leave the cell. Cells without such micropores, not allowing the molecules to escape, can be made to die by poisoning. This would incorporate additional autocatalytic networks into cell metabolism. Alternatively, within the cell wall catalytic centers can be generated as a response to an external stimulus as a templating molecule. Again, a competitive reaction chain has to be designed so that cells would be induced to die, when such molecules were not produced or accumulated. The developing protocells can in principle be trained to produce the desired waste product molecule, by autocatalytic generation of micropores or selective reaction centers as a response to an external stimulus as a templating molecule.
9.4 Control Parameters and the Emergence of Artificial Life
9.4.1 The Logistic Map
The design of a system that adapts its function by an evolutionary process, in our case the development of a cellular catalytically behaving system, raises an interesting question that was originally formulated by Descartes[25] : how can a designer build a device which outperforms the designer specifications? If specifications are followed too closely, there is no way that improvements can be made. On the other hand, if they are followed too loosely, the device will not operate according to specifications.
For most e cient evolutionary design, this implies that there will exist an optimum condition, at which the compromise of the two conflicting requirements is found. Langton defined a complexity parameter λ that determines such a condition[26].
We learned in Chapter 8 of excitable systems and active media and in the previous sections of this chapter of complex autocatalytic reaction networks. Computational systems have been designed[27] that provide insights into the general condition by which complex behavior emerges. A more general understanding of the dynamic features that determine complex behavior is obtained from analysis of the the so-called logistic map[28a]and Wolfram’s two-dimensional cellular automata studies[28b] .
It will appear especially from Wolfram’s work that a priori prediction of macroscopic behavior even for many particle systems that follow simple interaction rules is often not possible. The behavior can be sensitive to initial conditions and disturbances. These are, of course, conditions that are optimum for a learning system, where microscopic rules have to be adapted to macroscopic requirements. The optimum condition for emergence of life-like multiplication appears close to conditions where the system behavior becomes unpredictable. An important feature of a living cell is its finite lifetime. Sustained existence
380 Chapter 9
of a living collective system of cells is maintained by self reproduction.
In order to introduce the concept of a control parameter, we will analyze first the logistic map to illustrate more precisely the di erent phases of self organization that one can distinguish. We will follow closely the work by Nicolis[28a]. The logistic map is a generalized equation that describes the development of a population x due to growth and
decline by competition between the species: |
|
|
|
||
xn+1 |
= 4µxn(1 |
− |
xn) |
|
0 ≤ µ ≤ 1 |
|
|
|
0 ≤ x ≤ 1 |
||
where µ is a control parameter. The solutions x of the corresponding set of equations vary
qualitatively depending on the value of µ. When µ < |
1 |
−− |
|||
4 , only the trivial solution |
x = 0 |
||||
exists, and no growth is possible. In the interval |
1 < µ < 3 , the solution converges to a |
||||
unique value: |
|
|
4 |
4 |
|
|
1 |
|
|
|
|
|
−− |
|
|
|
|
|
x = 1 − |
|
µ |
|
|
|
4 |
|
|
||
−− |
|
|
|
|
|
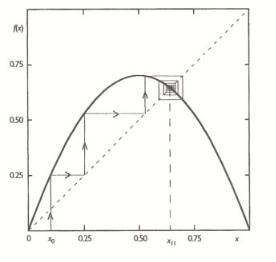
Its path towards x = n→∞xn is illustrated in Fig. 9.6. The solution is at the |
cross- |
||||
section of diagonal f (x) = x and the inverse parabola. The subsequent values of xn are the cross-section of the respective vertical lines with the parabola. After an initial onset,
−−
the numbers xn spiral to x , with increasing value of n.
Figure 9.6. Evolution toward the stable fixed point in the logistic map for µ = 0.7[28a].
A qualitativily very di erent behavior is observed when µ > 34 .
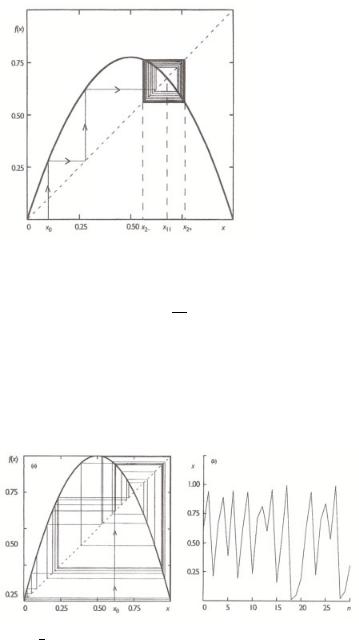
An example of such behavior is sketched in Fig. 9.7, for µ = 0.775. Now two solutions
−−
exist for x :
x2+ = 4µ x2− (1 − x2−) x2− = 4µ xx2+ (1 − x2+ )
Heterogeneous catalysis the origin of life, biomineralization |
381 |
Figure 9.7. Evolution toward a stable cycle of order two in the logistic map for µ = 0.775[28a].
with solutions
x2± = 1 1 + 4µ ± (16µ2 − 8µ − 3)1/2 8µ
After an initial period, the solutions at infinite n iterate between x2+ and x2− . This phenomenon is called period doubling.
In the regime 34 < µ < 1 an infinite sequence of successive period doublings occurs at increasing values of the control parameter µ(µ1 = 34 , µ2, ....., µn) culminating at a well-defined value µ∞ < 1.
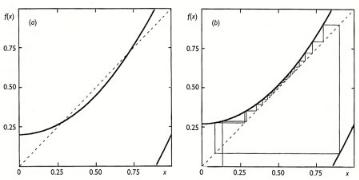
The logistic map at µ = 1 generates di erent chaotic behavior (see Fig. 9.8).
Figure 9.8. Fully developed chaos in the logistic map for µ = 1: (a) successive iterations starting from
√
x0 = ( 5 − 1)/2; (b) time series generated by these iterations[28a].
In some systems an additional interesting phenomenon, called intermittency, appears when the functions f (x) as in Fig. 9.6 are close to curve at f (x) = x. This is illustrated in Fig. 9.9 for a particular function f (x). After a short transient in the narrow region between the graph and bisector, the process resembles convergence to a fixed point that
382 Chapter 9
Figure 9.9. Generation of intermittent behavior through limit point bifurcation in the map f (x) = 0.25 + ε + x2 mod 1: (a) ε = 0.55: the system possesses one stable and one unstable fixed point; (b) ε = 0.02: the fixed points have been destroyed and the system undergoes chaotic bahavior of the intermittent type[28a].
is nearly stable. It therefore has a long time scale. However, the iterations will eventually leave this region and evolve to another branch of the graph of f (x) and be reinjected back to the region of near tangency.
This will appear as a series of long periods of quiescence interrupted by short-lived bursts. This phenomenon is called intermittency and is a signature of turbulence. It is a well-known phenomenon that occurs, for instance, for mass flow in trickle flow reactors at flow velocities where flow becomes turbulent.
The change in dynamic behavior as a function of control parameter can be considered analogous to the phase behavior of a material. For instance, as a function of temperature, water will go through a highly ordered state, ice, to an intermediate disordered state water, and finally to a gas state of complete disorder.
9.4.2 Life at the Edge of Chaos
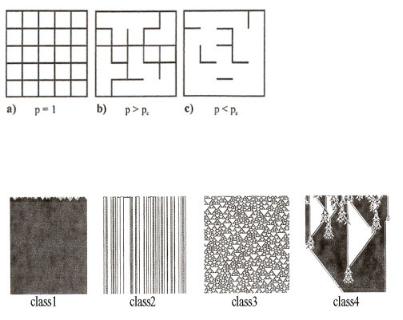
Emergent behavior occurs in many systems. For catalysis in porous systems bond or site percolation is an important example. It describes the probability that in a statistical network a particle can move through the system. It models the mass transport through a porous medium. This is illustrated in Fig. 9.10[29], where a two-dimensional network is shown with all points connected. At some specific point, the number of bonds that are broken is high enough that the statistical probability of finding a network that completely spans the lattice, Pc, is enough small that there are only disconnected clusters. The overall connectivity at this point is lost and percolation is no longer possible.
Wolfram[28b] discovered analogous behavior from simulation studies with cellular automata. His work shows that, notwithstanding well-defined short-range interaction rules between components on a microscopic level, macroscopic dynamic behavior can become unpredictable. This implies that external disturbances can have an important outcome on both temporal and structural events. This is consistent with a condition of life, where there is change due to evolutionary response. Examples of the four basic classes of behavior Wolfram discovered are shown in Fig. 9.11.
In Wolfram’s computational work pattern formation is studied on a two-dimensional lattice. Interaction rules are defined between lattice squares for the evolution of blackness
Heterogeneous catalysis the origin of life, biomineralization |
383 |
Figure 9.10. Bond percolation: (a) all bonds are closed; (b) part of the bonds are open, but there is still a cluster of infinite size; (c) there exist only clusters of finite size.
Figure 9.11. Examples of the four basic classes of behavior seen in the evolution of cellular automata from from random conditions. Adapted from S. Wolfram[28b].
or whiteness of a square on the lattice starting with an initial condition in the first row at the top of the system defined by a particular sequence of black and white squares. One then moves downwards in successive rows. The coloring of an element in each successive row depends on the coloring of neighboring and next neighboring elements in the previous row.
Hence rules have been set up in which the color of the cell in a row n depends on the coloring of the three neighboring cells in row n − 1. Each system is determined by eight di erent rules. In total, 256 di erent choises can be made, generating an amazing variety in pattern behavior. Wolfram distinguishes four classes of behavior.
–Class 1: All initial conditions lead to exactly the same result. Initial di erences die out rapidly.
–Class 2: There are many di erent final states, but all of these consist of simple structures, that remain the same for ever or repeat. Changes due to di erent initial conditions may persist but remain localized.
–Class 3: behavior is complicated and seems, in many, respects random, although nested structures such as triangles and other small structures always tend to appear. There is a rapid increase in network complexity. Changes in initial conditions spread everywhere, as in a percolating system. There is long range communication but there is no repetitive behavior. Changes are irreversible.
–Class 4: There is a mixture of order and randomness. Localized structures are formed, but move around and interact in complicated ways. Structures persist but are floating, they change sporadic. Long range communication is lost. The patterns formed are extremely sensitive to initial conditions.
384 Chapter 9
Representative structures from all four of these classes are shown in Fig. 9.11. We recognize the overall changes in behavior from complete order to disorder and intermediate stages with several stationary solutions. What is new are the stages with intermediate structure formation, decay and reappearance. The first three catagories of Wolfram can be identified with the three types of behavior we have met in the logistic map model of a continuous dynamic system. Class IV behavior with long transient and complex patterns of localized structures has no direct analog. The scene is now set for a return to the theories of the origin of life.
Following the ideas of Anderson[27] , Langton[26], who is one of the founders of artificial life research, coined the phrase “life at the edge of chaos”. To identify the condition of life for a cellular automaton system, he defined a control parameter λ. For a cellular automaton with K states and N neighbors the λ parameter is defined as follows. An arbitrary state Sq is chosen as a quiescent state, as for instance, the solution zero, with µ < 14 for the logistic map. If there are nq transitions defined to state Sq , the remaining KN − nq can be filled randomly and uniformly over the other K − 1 states, where
λ = KN − nq KN
If λ = 0, all the transitions in the system create the quiscent state Sq . This implies full order. When λ = 1 as the point where all of the states are filled randomly and there is complete disorder.
Langton considers that in a living system the dynamics of information has gained control over the dynamics of energy. Langton suggests that information can dominate, the dynamics of physical systems in the vicinity of a second-order (or critical) phase transition.
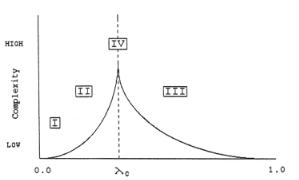
At intermediate values of λ, a phase transition can occur between periodic and chaotic dynamics. At either end of the λ spectrum, behavior seems simple and predictable. It is the behavior in the vicinity of this phase transition that is complex and unpredictable. There are long transients, intermediate and sometimes periodic structures. They are generated and later collapse, very similar to the class 4 system of Wolfram.
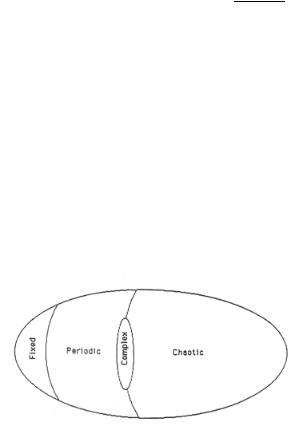
The dependence of the di erent phase space regimes on λ is illustrated in Fig. 9.12, in which the four Wolfram class of behavior are indicated.
Figure 9.12a. Schematic drawing of cellular automaton rule spaces indicating relative location of periodic, chaotic and complex regimes[26].
Heterogeneous catalysis the origin of life, biomineralization |
385 |
Figure 9.12b. Schematic drawing of complexity versus λ over CA rule space, showing the relationship between the Wolfram classes and the underlying phase-transition structure[26].
Approaching the transition from “below”, one progresses from simple fixed-point to simple periodic behavior, accompanied by larger and longer transients showing more and more sensitivity to the array size, until the transition regime is reached. The slow growth and occasional collapse of complex dynamics to periodic behavior makes the outcome of a particular rule operating on a particular configuration impossible to predict in the general case. Just slightly past the transition regime, the ultimate collapse to periodic behavior becomes extremely rare for finite arrays. Ultimately, the behavior becomes maximally chaotic and, hence, again predictable.
Living systems, according to Langton, can probably best be characterized as avoiding
−−
attractors, as the values x i in the logistic map, towards which the solution converge or oscillate. In the periodic system such attractors exist and are characterized as limit cycles or fixed-point attractors towards which the system converges with time. In the chaotic regime attractors can also exist, and are known as strange attractors typically of a high dimension. Living systems have learned to maintain themselves on extended transients, near a critical transition, where the state remains undecided. This is also illustrated by the simulations discussed in the Chapter 8, page 345, on replication near system phase boundaries, when the fluctuations in concentration in time and space are large.
When one exceeds a particular complexity threshold, the autocatalytic networks must give rise to the emergence of a self sustaining network. A metabolic system crystallizes that is able to replicate by division. There is, however, a limit to such complexity for reproducing systems. As we discussed in the previous section, once complexity passes another critical parameter, replication requires coding of the instructions in a program, as von Neumann proposed for his self-reproducing computer and life realized through the DNA genetic system.
9.5 Di erent Levels of Self Organization in Catalysis; a Summary
In Chapter 8, we described how combinatorial evolutionary processes optimize the system by adaptation to a template. In the have been formed they can be reproduced.
In the previous sections we have analyzed computational models of artificial chemistry that indicate that, in principle, the chemistry can be designed so as to create an artificial catalytic system, that optimizes its selectivity by evolutionary adaptation.
The ultimate catalytic design would be the generation of such an artificial catalytic
