Molecular Heterogeneous Catalysis, Wiley (2006), 352729662X

356 Chapter 8

Figure 8.13. Silicate oligomers as identified in waterglass solution. Neutral oligomers are shown.

Figure 8.14. The oligomers formed in the presence of tetrapropylammonium cation[28].

vary with the concentration of the basic cation and the reaction conditions. When organic cations are present, the interaction of the hydrophobic molecule with silicate oligomer can become fairly strong, especially when the oligomer dimensions and template size become comparable. The tetrapropyl cation is the preferred cation in silicalite synthesis. The tetrapropyl cation is shown schematically attached to various silicate oligomers in Fig. 8.14. A special cluster appears to be the Si33 cluster shown in Fig. 8.15.

The clusters in Figs. 8.14 and 8.15 have been assembled from oligomers as shown in Fig. 8.13, by a process which is driven by the specific stabilizing interaction of the tetrapropylammonium cation and silicate cluster. The Si33 cluster apparently has an optimum interaction between the tetrapropyl ion and the silicalite cage. It is the result of self assembly

Self Organization and Self Assembly of Catalytic Systems 357

Figure 8.15. The Si33-tetrapropylammonium precursor complex.

by a molecular recognition process between silicate oligomers and tetrapropylammonium cation. The equilibria that exist between the di erent solution oligomers shift towards the Si33 cluster. Formation of this intermediate already occurs under relatively mild reaction conditions. Its formation process can be considered evolutionary, in the sense that interaction between template and silicate oligomers selects the desired oligomers and rejects those that do not give the preferred interaction. Under zeolite synthesis conditions the Si33 precursor molecules, formed around the tetrapropylammonium ion, dimerize and condense into partially organized precursor species that can be considered as the nanoblocks shown in Fig. 8.16.

Interestingly, the local environments of the tetrapropylammonium ion in the Si33 precursor and of tetrapropy ammonium in silicalite are slightly di erent. The Si33 environment resembles that of a channel, whereas the tetrapropylammonium ion occupies a channel cross-section in silicalite. The need to reorient the tetrapropylammonium ions when the zeolite crystal is formed may necessitate the intermediate formation of nanoslabs. The dimensions of these nanoslabs depend on the reaction conditions. Their size is typically 4 x 4 x 1.3 nm or 4 x 2 x 1.3 nm. The number of 33 cluster rows varies in this example by a factor 2.

In situ X-ray scattering studies have convincingly shown (Fig. 8.17) that only when nanoblocks reach a significant concentration does zeolite crystallization occur. Zeolite crystallization, hence, does not occur directly from the monomer, but its complex unit cell structure requires formation through stages. Initially a specific precursor molecule is to be formed. In the case of silicalite, this is the Si33 cluster. In a second stage, the precursor molecule self assembles into nanoblocks of approximately the unit cell dimension of the silicate, developing its key geometric motif. The size of the nanoblocks is controlled by colloid-chemical properties. It depends on the double potential of the negatively charged silicate clusters with counteracting adsorbed and dissolved cations[31]. A higher temperature is needed to overcome the double potential barrier so that the nanoblocks can

358 Chapter 8

Figure 8.16. Proposed schematic structures for the silicalite MFI-type zeosil nanoslabs. The Si33 precursor can self assemble to form discrete and organic–inorganic hybrid nanoslabs with dimensions depending on synthesis conditions[29].

Figure 8.17. Time-dependent scattering curves of silicate formation in the homogeneous phase, followed by small angle and wide angle scattering[30].

crystallize.

The type of precursor molecule formed depends on the templating molecule. This key step is described as a molecular recognition event. When the templating molecule is chosen to resemble a key intermediate of a reaction that the zeolite should selectively catalyze, a zeolite structure crystallizes that contains cavities with optimum fit for that reaction intermediate.

8.8 Evolutionary Computational Methods

In this section, we will begin with a short exposition of di erent evolutionary computational approaches. Then we will apply one of these methods to the design an alloy catalyst with optimal performance for a particular dissociation reaction. The performance of the catalyst is theoretically tested using the dynamic Monte Carlo method to predict the kinetics for a surface reaction.

Self Organization and Self Assembly of Catalytic Systems 359

Evolutionarycomputation (EC) is a term used to denote a group of methods from computer science that mimic natural evolution [32,33]. These methods are mainly used in optimization problems. All EC methods have some common properties. They usually work with a set of objects that represent the object that one wants to optimize (parameters, a structure, or a process). The set of objects is called a population and the objects are individuals. An individual is represented in some coded form. The encoding is often the genotype and the object itself the phenotype. Working with a (large) number of objects at the same time helps in obtaining a global instead of a local optimum.

EC improves a population by three genetic operations: selection, mutation, and crossover. Selection does what its name implies. It picks out those individuals that are allowed to reproduce and to make a new population. Other individuals are discarded. Reproduction proceeds via the combination of two individuals by a crossover. Parts of the genetic materials of the individuals are chosen and put together to form one or two new individuals. The idea is that the good parts of the genetic material of di erent individuals can be combined in this way. Finally, the genetic materials can be more or less arbitrarily changed. This is called mutation and it is used to prevent premature convergence to a local optimum. The advantages of EC methods are that they provide more of a global optimization rather than a local optimization. In addition, they can also be used to optimize non-numerical objects. They are also very good at scanning large search spaces. This means that they can be employed to optimize objects with many components. They are also able to handle so-called NP-complete problems (NP stands for non-polynomial). These are problems that scale faster than a power of the size of the problem. An example of such a problem would be the optimization of the structure of a bimetallic catalyst. Each atom can be either one of two metals. With N atoms in the unit cell this give 2N possible structures, so the problem scales exponentially with the size of the unit cell.

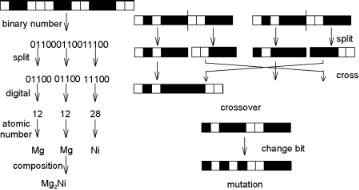
Figure 8.18. Example of a string of bits representing the composition of a bimetallic catalyst on the left. The standard crossover and mutation of genetic algorithms is shown on the right.

A drawback of all EC methods is that they can be computationally intensive. Important are the di erences between di erent EC methods. The EC method that has been used most in chemistry and chemical engineering is genetic algorithms (GA). There are other methods, however, that can be much more e cient. The most important di erence between the EC methods is the way in which an object is encoded. GA uses a string of bits. Figure 8.18 shows how this can be used to encode the composition of an alloy.

360 Chapter 8

The figure also shows how crossover and mutation can be done with such an encoding. Theoretical work on GA has shown that the method will find global optima and why it is capable of searching in a very large search space. Computer experiments have shown that an encoding and genetic operators that reflect properties of the objects that are to be optimized can lead to much faster convergence. In genetic programming, the encoding can use data structures (usually trees or graphs) that can adapt themselves. The idea is that an encoding evolves that is best adapted to the object to be optimized.

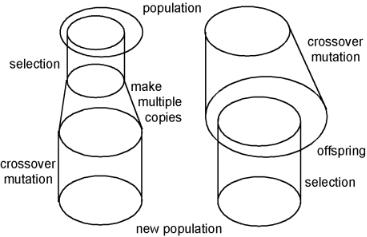
Another di erence between EC methods is the order in which the genetic operators are applied. Figure 8.19 shows the two main variants. In GA there is first a selection. The number of individuals is then increased, by taking the best individuals more than once so that the same number of individuals is obtained as in a full population. Finally, a new population is constructed by crossover and mutation.

In evolution strategies, a method that is well suited for parameter optimization, crossover and mutation is used first to generate a large number of o spring. Selection is then used to reduce the o spring to a new population. The selection can include the old population or not, and there are many di erent methods to make the selection.

Figure 8.19. Ordering of the genetic operators as in genetic algorithms (left) and in evolution strategies (right).

The selection process is the place where the optimization in EC methods really takes place. This is where methods such as dynamic or kinetic Monte Carlo (DMC) simulations become important. They are used to compute the properties of a system or process. These properties are then converted to a fitness value. This fitness value is for satisfaction of a particular requirement of performance which is then operated on by the EC methods. The conversion is di erent for each system and property and also determines how e ective the selection is. Dynamic Monte Carlo simulation, as we have already discussed, is a method to simulate elementary processes along with the actual rate. The method uses each individual reaction as an elementary event, which means that time scales comparable to actual experiments can be simulated. The reaction rate constants that it needs as input can be calculated using quantum chemical methods such as density functional theory, which results in what has been termed ab initio kinetics (see Chapter 3.10.4).

Self Organization and Self Assembly of Catalytic Systems 361

The application of such methods to the modeling of overall kinetics has been described in detail in Chapter 3. EC and DFT can be combined to investigate the e ect of replacing atoms or chemical groups by others. The simplest application would be to have the EC determine only the composition. This might be done with a straightforward GA. The coding can be done more or less as shown in Fig. 8.18.

The genotype consists of a number of parts each of which correspond to an atom (or molecule). In principle, standard crossover and mutation can then be used; e.g., this has been the procedure followed by the group of Nørskov to find new super-strong alloys [34]. Computer experiments have shown that adapting crossover and mutation to the problem can speed up that optimization. The combination EC plus DMC can also be used to carry out structural optimizations.

We will illustrate here the generation of an optimum alloy surface configuration for the reaction of 2A + 2B → 2AB[35].

There is a bimetallic surface with two types of sites. As will adsorb on only one type (α), and Bs only on the other type (β). The specific application of such a system might be CO oxidation, where A refers to CO and B2 refers to O2. The adsorption of Bs is a dissociative one. The reactions in the model therefore are the following.

A(gas) + α −→ A(ads)

B2(gas) + 2β −→ 2B(ads)

and

A(ads) + B(ads) −→ AB(gas) + α + β

or if we only look at how the site occupation changes:

α −→ A 2β −→ 2B

and

A + B −→ α + β

Here α and β are both vacant sites, but of di erent type. A and B in the last reaction should be nearest neighbors. The rate constants of the adsorption of A, B and the surface reaction are Wads(A), Wads(B) and Wrx , respectively. We consider the case here where the

adsorbate does not di use. For Wads(A)/Wrx = 0.2 and Wads(B)/Wrx = 1 the optimal structure was determined using a genetic algorithm. The structure of the surface was coded as a

string of bits (0s and 1s) as follows. A 0 represented an α site, a 1 a β site. A string represented all sites in a unit cell. The size and shape of the unit cell was fixed for each optimization run with the genetic algorithm. Runs were done for square unit cells with 2 x 2 to 8 x 8 adsorption sites. The structure of the whole surface was obtained by periodic repetition of the unit cell. Figure 8.18 shows how we got from the string of bits to the structure cell. The string of length 25 represents a 5 x 5 unit cell. The 25 bits are first split into five groups of five. These groups are put into a square, and each bit is replaced

362 Chapter 8

Figure 8.20. The optimum topology of AB alloy for catalysis reaction 2A + 2B → 2AB[35].

Figure 8.21. Representation of Pt–Au(100) alloy surface optimum for selective decomposition of NO in presence of excess oxygen[36].

by its adsorption site. This gives us the unit cell, which is repeated periodically to obtain the whole surface.

A typical optimization run used 64 strings per generation and had 50 generations. New generations were obtained from old ones by the usual selection, crossover and mutation. Typical crossover probabilities were 0.02 per bit. The rate of AB formation was used to make the selection, but it was scaled linearly so that the best string in a generation had a probability of being selected that was 3.5 times the probability for an average string. Selection was done using remainder stochastic sampling. The resulting optimum structure is shown in Fig. 8.20

One third of the sites are β sites and two-thirds are α sites. All β sites occur in pairs. (Isolated β sites are not found, because B2 needs at least two neighboring sites

Self Organization and Self Assembly of Catalytic Systems 363

for adsorption). Half of the α sites have one β neighbor and the other half have two β neighbors in both structures. The paired β sites now have an optimum contact with α sites.

Interestingly, detailed dynamic Monte Carlo studies of realistic systems indeed indicate the relevance of such detailed type of surface topologies. Kieken et al.[36]. studied the decomposition of NO to N2 in excess O2 over Pt/Au alloys. They deduced that an alloy which is comprised of a Pt ensemble assembled into a “+” structure surrounded by Au atoms as is shown in Fig. 8.21 is more active. The cluster ensemble of Pt atoms is made up of bridging Pt sites that will adsorb NO but help prevent O2 dissociations. The bridge sites share metal atoms, which makes it very unfavorable for it to accommodate the two strongly bound O atoms that would result. O2, therefore, is di cult to dissociate since two oxygen atoms cannot be accommodated. NO dissociation is also hindered. However, two NO molecules can adsorb and recombine in an associative reaction to give N2O and adsorbed oxygen. N2O can readily decompose in a consecutive reaction step to give N2 and adsorbed oxygen. The latter atoms will recombine to give molecular oxygen by surface di usion. By patterning the surface we can help the surface to separate the product species which can poison active sites.

8.9 Summary

The complexity of the catalytic event has been analyzed in this chapter in great detail. First elementary reaction steps at an isolated reaction center have been considered

and then the increasing complexity of the catalytic system when several reaction centers operate in parallel and communicate. This situation is common in heterogeneous catalysis. On the isolated reaction center, the key step is the self repair of the weakened or disrupted bonds of the catalyst once the catalytic cycle has been concluded. Catalytic systems which are comprised of autocatalytic elementary reaction steps and communication paths between di erent reaction centers, mediated through either mass or heat transfer, may show self-organizing features that result in oscillatory kinetics and spatial organization. Theory as well as experiment show that such self-organizing phenomena depend sensitively on the size of the catalytic system. When the system is too small, collective behavior is shut down.

Complexity features of catalytic phenomena have obtained a firm basis. All the ingredients to predict catalytic reactivity as a function of catalyst composition and structure are available. A strategy to optimize the catalyst reactivity is in place.

The outline of an adaptive approach has been given based on evolutionary combinatorial principles. The theoretical combinatorial approach at the end of the chapter is introduced with a summary of the biological immunoresponse system. This is of great interest because it exemplifies evolutionary dynamics of an adaptive system consisting of many components, that can self assemble a catalytic system optimized for the catalytic reaction of choice. Since the mechanism of zeolite synthesis can be viewed as being mechanistically related, this topic is discussed here. Molecular recognition and self assembly of di erent catalyst precursor aggregates directed by template molecules are present in such a system, but the amplification shown by the immunoresponse system is lacking.

Evolutionary adaptation has been used experimentally in biological systems to optimize enzyme performance. The use of combinatorial self learning computational approaches has been illustrated for the optimization of the composition of alloy catalysts by simulating catalytic performance using the dynamic Monte Carlo approaches.

364 Chapter 8

References

1.M. Neurock, R.A. van Santen, J. Am. Chem. Soc. 116, 4427 (1994)

2.E.M. Shustorovitch, Surf. Sci. Rep. 6, 1 (1986)

3.J.M. Thomas, C.R.A. Catlow, G. Sankar, Chem. Commun. 24, 2921 (2002)

4.(a) G. Belusi, M.S. Rigutto, in J.C. Jansen, M. St¨ocker, H.G. Karger, J. Weitkamp (eds.), Advanced Zeolite Science and Applications, Stud. Surf. Sci. Catal. 85, 177 (1994)

(b)P. Ratnasamy, D. Srinivas, H. Kn¨ozinger, Adv. Catal. 48, 1 (2004)

5.H.C.L. Abbenhuis, S. Krijnen, R.A. van Santen, Chem. Commun., 331 (1997)

6.R. Imbihl, G. Ertl, Chem. Rev. 95, 697 (1995)

7.L.M. Pecora, T.L. Carroll, Phys. Rev. Lett. 64, 84 (1990)

8.A.S. Mikhailov, Foundations of Synergetics I, Springer, Berlin (1994)

9.P. Gray, S.K. Scott, Chem. Eng. Sci. 38, 29 (1983); 39, 1087 (1984)

10.J. Pearson, Science, 261, 189 (1993)

11.R.J. Gelten, R.A. van Santen, A.P.J. Jansen, in Molecular Dynamics, P.B. Balbuena, J.M. Seminario (eds.), Elsevier, Amsterdam, p.737 (1999)

12.K-J.L. Lee, W.D. McCormick, J.E. Pearson, H.L. Swinney, Nature, 369, 215 (1994)

13.C.G. Langton, Physica D, 10, 135 (1984)

14.E.F. Codd,Cellular Automata, Academic Press, New York (1968)

15.H.M. Chou, J.A. Reggia, Physica D110, 252 (1997)

16.O. Arino et al., Mathematical Population Dynamics, Marcel Dekker, New York (1900)

17.M. Bowker, H. Houghton, R.A. Hadden, J.N.K. Hyland, K.C. Waygh, J. Catal. 109,

263 (1988):

K.C. Waugh, Catal Today, 15, 51 (1992)

18.V. Joh´anek, M. Laurin, A.W. Grant, B. Kasemo, C.R. Henry, J. Libuda, Science 304, 1639 (2004)

19.C. Branden, J. Tooze, Introduction to Protein Structure, Garland, p. 185 (1991)

20.(a) L. Stryer, Biochemistry, Freeman, New York (1995);

(b)E.A. Padlan, D.R. Davies, S. Rudiko , M. Potter, Immunochemistry, 13, 945

(1976)

21.W. Jencks, Catalysis in Chemistry and Enzymology, McGraw-Hill, New York (1969)

22.R.A. Lerner, S.J. Benkovic, P.G. Schulz, Science, 252, 659 (1991)

23.M.F. Reetz, K.E. Jaeger, Top. Curr. Chem. 200, 31 (1999); M.T. Reetz, Proc. Natl. Acad. Sci. USA, 101, 5716 (2004)

24.F.H. Arnold, Acc. Chem. Res. 31, 125 (1998)

25.R.A. Lerner, S.J. Benkovic, P.G. Schultz, Science, 252, 659 (1991)

26.D.W. Lewis, D.J. Willock, C.R.A. Catlow, J.M. Thomas, G.J. Hutchings, Nature, 382, 604 (1996)

27.C.L. Hill, X. Zhang, Nature, 373, 324 (1995)

28.C.E.A. Kirschhock, R. Ravishankar, F. Verspeurt, P.J. Grobet, P.A. Jacobs, J.A. Martens, J. Phys. Chem. B, 103, 4965 (1999)

29.C.E.A. Kirschhock, V. Buschmann, S. Kremer, R. Ravishankar, C.J. Houssin, R.A. van Santen, B.J. Mojet, P.J. Grobet, P.A. Jacobs, J.A. Martens, Angew. Chem. Int. Ed. 40, 2637 (2001)

30.P.P.E.A. de Moor, T.P.M. Beelen, B.U. Komanschek, L.W. Beck, P. Wagner, M.E. Davis, R.A. van Santen, Chem. Eur. J. 5, 2083 (1999)

Self Organization and Self Assembly of Catalytic Systems 365

31.C.E.A. Kirschhock, R. Ravishankar, P.A. Jacobs, J.A. Martens, J. Phys. Chem. B, 103, 11021 (1999)

32.K. Mainzer, Thinking in Complexity, Springer, Berlin (2003)

33.J.M. Holland, Hidden Order, Addison-Wesley, Reading, Mass. (1995)

34.G.H. Johannesson, T. Bligaard, A.V. Ruban, H.L. Skriver, K.W. Jacobsen, J.K. Nørskov, Phys. Rev. Lett. 86, 25506 (2002)

35.A.P.J. Jansen, personal communication;

A.P.J. Jansen, C.G.M. Hermse, Phys. Rev. Lett. 83, 3673 (1999) C.G.M. Hermse, A.P.J. Jansen, Surf. Sci. 461, 168 (2000)

36.L.D. Kieken, M. Neurock, D. Mei, J. Phys. Chem. 109, 2234 (2005)

37.C.S. Cundy, P.A. Cox, Microporous Mesoporous Mater. 82, 1 (2005)