Molecular Heterogeneous Catalysis, Wiley (2006), 352729662X

346 Chapter 8

Two areas can be identified: one with three steady states and another area to be characterized as excitable. At the boundary of the two time regimes transient patterns form in response to a small disturbance. In this unstable region a particularly interesting phenomenon is observed that behaves like cell multiplication. Patterns occur with concentration profiles of cellular form that grow and replicate. When these “cells” exceed a particular dimension, the interior destabilizes (in this case because a necessary concentration gradient is not maintained) and cells divide.

Figure 8.6. Time evolution of spot multiplication. This figure was produced in a 256 by 256 simulation

with physical dimensions of 0.5 by 0.5 and a time step of 0.01. The times t at which the figures were taken are as follows: (A) t = 0; (B) t = 350; (C) t = 510; and (D) t = 650[10].

The resulting spatio-temporal pattern at a particular point in this unstable region is shown in Fig. 8.6. The compositional profile in Figure 8.6 was made just after an initial square perturbation had decayed to leave four cell-like spots. Cell growth and division are shown to succeed. Experimental verification of such self replication has been given by Lee et al. [12] in a reaction system with ferrocyanide, sulfide and iodide that has a bistable stationary solution.

An element of an excitable medium returns to its initial state of rest after being activated by an external perturbation that exceeds a particular threshold. In an excitable medium this results in a traveling excitation pulse.

A bistable medium is converted into an excitable medium by coupling a production rate with an inhibitor component. An excitable medium undergoes a fast transition into an excited state if triggered by the threshold transgressing perturbation. After this transition, the medium at the point becomes refractory, slowly recovering its excitability until it again becomes receptive. Target patterns and spiral waves are characteristic resulting features.

Oscillatory media have many characteristics of an excitable medium. They consist of a large population of self oscillating elements, which are weakly coupled. Depending on the properties of the medium, oscillations can synchronize or desynchronise with time. The os-

Self Organization and Self Assembly of Catalytic Systems 347

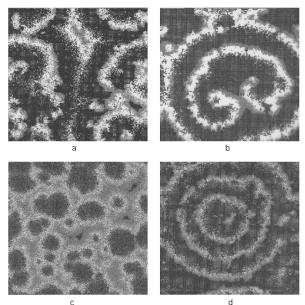
Figure 8.7. Four examples of spatio-temporal pattern formation obtained in dynamic Monte Carlo simulation of the reconstructing CO oxidation system: (a) turbulent patterns; (b) a double rotating spiral; (c) cellular structures; (d) target patterns[11].

cillations in rate and self organization of overlayer patterns observed for the CO oxidation reaction, discussed earlier, belong to this category. Di usion of CO synchronizes the different reaction sites on the surface. Otherwise, overall catalytic time-dependent behavior would be chaotic in time, controlled by the collision moment of the individual molecules. The need to couple the reaction phases at di erent catalytic reaction centers is neatly illustrated by dynamic Monte Carlo simulations on grids of varying size representing the reconstructing surface during the CO oxidation reaction [11].

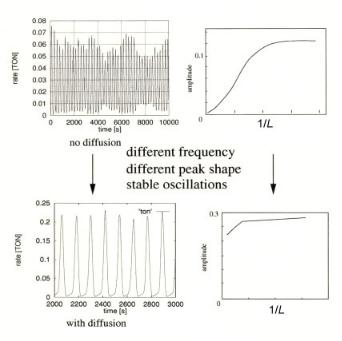
Di erent spatio-temporal patterns can emerge depending on the kinetics in this system. Figure 8.7, for example, presents turbulent double rotating spirals, cellular, and target patterns. In Fig. 8.7, reactions are represented by composition changes with a particular probability on grid positions, dependent on the occupation of neighboring grid positions. These figures illustrate self-organized surface pattern formation in the oscillatory medium of the catalytic oscillators. They appear as the result of colliding wave fronts of di erent local surface concentrations. The spatial dimension of these patterns depends on the square root of di usion rate and oscillation time. When the grid is small, the grid represents only a small number of surface atoms and, hence, can only support a single reaction center which requires enough surface atoms to allow for reconstruction. This results in only a single oscillation. When the grid size is increased, the possibility of more reaction centers arises. As Fig. 8.8b shows, in the absence of di usion there is no synchronization and the amplitude of the oscillation decreases rapidly with the dimensions of the grid system. Figure 8.8d shows, however, stable oscillations when there is di usion that covers a large fraction of the grids within the period of a catalytic cycle. Of course, there will be a limitation when the grid size becomes too large and time scales of di usion and local

348 Chapter 8

Figure 8.8. Simulation of the influence of di usion and grid size on overall oscilatorry behavior. L is the dimension of the grid. (a) and (b), absence of di usion. The frequency of the oscillations (a) does not change with grid size, but the amplitude of the oscillations (b) rapidly decreases with increasing grid size. (c) and (d(, with di usion; with di usion amplitude and shape of the oscillations change (c), but the amplitude of the oscillation is stable over a large grid size trajectory.

oscillation no longer match. Self organizing patterns will only occur in specific reaction condition regimes. For the CO oxidation reaction, such a condition arises when the temperature of the reaction is chosen just beyond the maximum of the overall reaction rate. In this temperature regime the auto catalytic reaction steps start to become rate limiting.

The assignment of reaction probabilities and di erent grid states as a function of the states of neighboring gridpoints can be considered as a specific case of cellular automata, on which a rich literature exists [13]. Cellular automata were originally designed by von Neuman to model self reproducing networks of cells. The von Neuman machine relied on the reproduction of a code that instructs the building of a machine, the analogue of cellular reproduction through the replication of DNA. He was able to construct such a machine in a cellular array with 29 states per cell and a five-cell neighborhood.

Later Codd [14] reduced the complexity of the Von Neuman machine inspired by insights in the physiology of the nervous system in animals. Important to our later discussion in Chapter 9 of the design of self organizing catalytic systems, he proposed a universal configuration of only eight-states per cell.

In 1997, Chou and Reggia [15] showed that it is possible to create cellular automata models in which a self replicatory structure emerges from a random density of individual components. Chou and Reggia designed the rules such that a viable structure of arbitrary size generated by a random process replicates and grows. This precedes the discovery of

Self Organization and Self Assembly of Catalytic Systems 349

Figure 8.9. Fourfold wave-symmetry obtained by a cellular automaton with square cells: (a) target pattern; (b) spiral wave. Adapted from O. Arino et al.[16].

self organization in the grid model dynamic Monte Carlo simulations of the CO oxidation reaction shown in Figs. 8.7 and 8.8.

Cellular automata simulations on the periodic grid neatly illustrate for an excitable medium how a two-dimensional automaton leads to target patterns or spiral waves (see Fig. 8.9). It is assumed in this automaton that all eight neighbors of an excited cell (block) become excited in the next step, except for the neighboring cells that become refractory (dashed), i.e. do not change. An excited cell becomes refractory after one time step and receptive (white) after two time steps. The simple mechanism that generates the target and spiral wave patterns illustrates that the key to self organization is the rules of interaction between neighboring sites. We will return to this subject in the next chapter.

8.5 Size Dependence and Cooperative Behavior

Phase transitions such as order–disorder transitions have a well-defined critical temperature when a system is su ciently large, so that boundary e ects can be ignored. An example of a disorder–order transition for a surface overlayer system is the mixing or demixing that occurs in a surface phase when repulsive interactions between adatoms dominate. At low temperatures two di erent phases demix and above a critical temperature a mixed phase can be formed. In the oxidation of methanol catalyzed by Cu, overlayers consisting of separate islands of oxygen atoms and adsorbed methoxy species are formed[17]. Reaction occurs only at the boundary of the two surface overlayer phases. The oxygen islands are formed from an oxide overlayer in which the free metal surface has reconstructed resulting in e ective attractive interactions between adsorbed oxygen atoms.

Surfaces of small particles have small dimensions. Such surfaces of small dimensions are present on stepped surfaces with short terrace length. With such small dimensions, no sharply defined critical temperature for phase separation exists and an intermediate surface state with partial ordering over a wide temperature interval can be formed.

In the previous section we noted that synchronization of reaction events that occur at di erent parts of a catalyst is a necessity for an oscillatory time dependence of reaction kinetics. The cooperative phenomenon called self organization can then take place. When particles become so small that only one catalytic cycle takes place per particle, synchronization is lost and no such self organization can occur.

A precondition for oscillatory behavior is the bistability of di erent surface phases. Under stationary conditions on Pd, the oxidation of CO to CO2 can give rise to hysteresis

350 Chapter 8

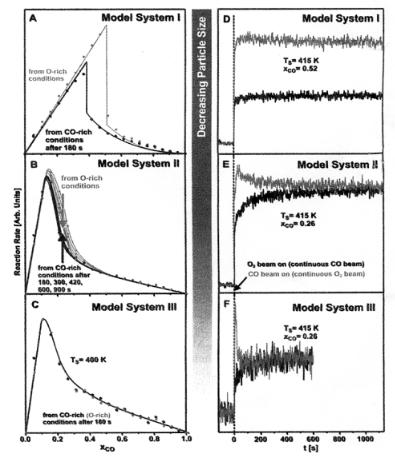
Figure 8.10. Particle size-dependent bistability and hysteresis. (A and D). On model system 1 (500 nm paricles), the CO oxidation shows a perfectly stable bistability behavior. On the time scale accessible by the experiment (>103 sec), one can arbitrarely switch between the two states by pulsing either pure CO or O2 . (B and E) For the model system II (6 nm particles), a very slow transition toward a single global state is observed in the transition region between the COand O2 -rich reaction regimes. This is accelerated by the presence of defect sites. (C and F). For the smallest particles of the model system III (1.8 nm), globally monostable kinetics are rapidly established under all conditions [for all experiments, the total flux of CO and O2 beams at the sample position was equivalent to a local pressure of 10−4 Pa;

surface temperature in (A) to (C), 400 K; (D) to (E), 415 K; the continuous curves in (A) to (C) are only a guide to the eye[18].

phenomena depending upon the O2/CO ratio in the system. The two phases are a CO rich overlayer phase and alternatively an oxygen-rich overlayer phase. On large particles the dependence of rate on increasing O2/CO ratio is di erent from the dependence found when one starts with a high O2/CO ratio and then this ratio is decreased. This behavior has been studied as a function of Pd particle size by Joh´anek et al.[18]. As shown in Fig. 8.10, the hysteresis loop appears when the particle size exceeds 6 nm. When the particle size decreases there is a smaller number of surface atoms and, as a result, the surface

Self Organization and Self Assembly of Catalytic Systems 351

phase composition now shows large concentration fluctuations that are non-synchronized. Phase separation is now suppressed.

The phenomenon of altered cooperative kinetic behavior as a function of surface dimension may be quite general. It will apply to those situations where surface overlayer island formation occurs with di erent kinetics than predicted within mean field kinetic expressions, in which ideal mixing of the surface overlayer is assumed. For instance, the electrochemical butterfly-type current–voltage diagram measured for sulfate adsorption (Chapter 3, Section 3.10.4), is significantly changed when a surface is taken with short terraces. The order–disorder transition on the extended terraces is responsible for the butterfly pattern. On shorter terraces, the well-defined features are no longer present and the sharp order–disorder transition no longer occurs.

8.6 Immunoresponse and Evolutionary Catalysis

The aim of theoretical catalysis is to predict catalytic reactivity for an arbitrary system and, hence, to direct the synthetic chemist to the exploration of new materials. A completely di erent approach, with important modeling consequences, would be possible if systems could be developed that not only self repair during the catalytic reaction, but also would change or adapt as a function of the product formed. The ideal catalyst would form itself from catalyst building components in a reaction mixture in response to desired products. To analyze the conditions for the chemodesign of such systems is one of the great challenges of modern catalysis. We refer further to this topic in Chapter 9.

Natural systems that are able to adapt to a desired product are the antibodies in biochemical systems. Their modular composition makes combinations in many di erent configurations possible. For instance, the macromolecular biological immunoglobulin system contains a great variety of compounds that vary in shape and size that can be organized to recognize a reagent by combinatorial association. More than 108 di erent antibodies can be formed.

Figure 8.11a. The shape of immunoglobulin G. Adapted from C. Branden and J. Tooze[19].

Antibodies are synthesized by cells as a cellular response to a foreign molecule (antigen). Antibodies are made specific for that antigen and reproduced by triggering cell division. The bio-immunoresponse reaction has been used to produce catalytically active immunoglobulin catalyst molecules by the use of antigen molecules with a shape and charge distribution close to those of the transition state of a desired reaction. Cells of the immune system produce a pool of antibodies by genetic recombination. Antibodies discriminate themselves by their unique combination of amino acids. They form large folded polypeptides that bind virtually any natural or synthetic molecule. In the genetic recombination process the genes encoding each antibody are spliced and recombined from

352 Chapter 8

Figure 8.11b. The Fa and Fab domains of immunoglobuline. Adapted from C. Branden and J.Tooze[19].

Figure 8.11c. Binding of phosphorylcholine to an antibody-combining site. Adapted from E.A. Padlan et al.[20b].

a battery of gene segments, which enable an organism to produce a multitude of di erent antibody molecules.

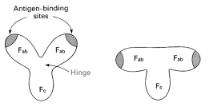
As generally described by L. Stryer [20a] and more specifically by Padlan et al.[20b], immunoglobulin has the shape of the letter Y (Fig. 8.11a). The antigen combines with the two Fab units, that have so-called segmental flexibility which enhances the formation of antibody–antigen complexes. Figure 8.11b shows the immunoglobulin domains Fa and Fab that consist of two sheets of antiparallel β strands. The sheets are bridged by a disulfide bond. The variable Fab units contain two additional β strands. Three key loops compose the complementary-determining regions (CDR) that form part of the antigen binding site. The detailed structure of the binding of phophorylcholine to an antibodycombining site is shown in Fig. 8.11c.

Self Organization and Self Assembly of Catalytic Systems 353

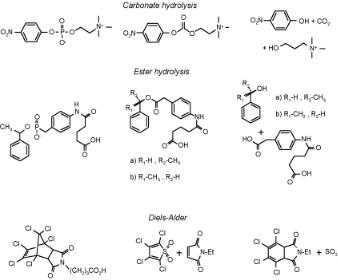
Figure 8.12. Picture of transition states, antigen with transition state analogous to transition states for the hydrolysis of carbonates and esters and Diels–Alder reaction. Adapted from R.A. Lerner et al.[25].

The structure of the antigen–antibody binding site shows a highly structure-dependent interaction that is dominated by hydrogen bonds and van der Waals and electrostatic interactions.

In response to a specific antigen, a particular antibody molecule is selected and amplified through the cellular system. Jencks[21] suggested that antibodies could be used as catalysts by selective stabilization of rate-determining transition states on a reaction pathway. Lerner et al.[22] showed that catalytic antibodies can be converted into selective catalysts induced by antigens with the shapes of transition states of a desired organic conversion reaction. They used amongst others tetrahedral, negatively charged phosphate and phosphonate transition-state analogues of the transition states for the hydrolysis of carbonates and esters. Many catalytic antibodies have been generated for a wide range of catalytic reactions.

An alternative biological approach is the use of evolutionary adaptation. An evolutionary biological implementation of the combinatorial adaptational approach towards the generation of improved and novel enzymes has been developed by Reetz and Jaeger[23] and Arnold[24]. Bacteria are used to produce catalytic proteins encoded by evolution of mutated genes. Mutations are introduced by the biochemical polymer chain reaction or other random mutagenesis methods. Recombinative techniques such as DNA shu ing are also used. Gene evolution is then carried out by selection or screening to identify a large library of potential genes, that will produce the desired biocatalyst. This directed evolution approach, for example, has been used to develop bacterial lipases with significantly enhanced enantioselectivity. In this approach to catalysis, no mechanistic information on the catalytic reaction is used to optimize the system. The desired catalyst is found by feedback of the information obtained by screening into the selection of the bacteria possessing the desired gene sequences.

These two approaches illustrate the impressive state of biomolecular catalysis, which

354 Chapter 8

has successfully developed approaches to direct a catalytic system towards optimum performance for a particular reaction. Molecular recognition (as in the immunosystem) and evolutionary adaptation by combinatorial self learning techniques are important principles that can be used in the design of an adaptive catalytic system. Once a preferred system has been generated, a mechanism should be in place for its amplification. In biological systems the cellular reproductive system serves this purpose.

Catalytic modeling can be used to assist identification of the proper testing molecule for the evolution of the desired catalytic system. An important goal in modeling e orts is the prediction of the shape of the transition state of a particular desired reaction step. We discussed this in some detail in previous chapters. In some instances the optimum shape of a transition state is dominated by the reaction complex itself, rather than by the interaction of the substrate with the catalyst. This happens to be the case for zeolite and enzyme systems. In contrast, for transition-metal catalysts the interaction between the substrate and the catalyst dominates the shape of the transition state.

Modeling of catalytic systems requires the ability to di erentiate between changes in surface structure and surface composition as well as three-dimensional structural aspects. As we have already discussed dynamic Monte Carlo simulation and ab initio quantum mechanical methods can be used to model adsorbate surface interactions and changes in surface structure and composition. Molecular mechanism and structured Monte Carlo simulation methods can be used to model three-dimensional aspects such as shape selectivity. Taken together, these methods can be used to model catalytic performance for a host of materials including metals, zeolites, metal oxides and metal sulfides. This was discussed in Chapters 3–5. These methods allow one to predict the overall rate of a catalytic reaction as a function of catalyst composition and structure. Recent genetic algorithms or related combinatorial evolutionary techniques can be used in conjunction with “predictive simulation methods” in order to modify the catalytic model system, computationally test the system for catalytic performance and begin to “design” more active material structures and compositions. This approach will be discussed in the Section 8.8 on Evolutionary Computation Methods.

Inorganic systems are much less sophisticated than the immunoresponse system, but similar in that, in principle, information on the transition state through the correct choice of template can be incorporated into the catalytic system such as in the case of zeolite synthesis. The mechanism of the zeolite synthesis reaction, discussed in the next, section has combinatorial evolutionary characteristics.

In Chapter 9, we summarize the current understanding of the origin of living cell system early in the evolution of life as an orientation on the question of, whether an artificial cell-type reaction that self assembles can be designed to optimize the rate and selectivity of catalytic reactions by an adaptive evolutionary process.

8.7 Inorganic Self Assembly Processes; Zeolite Synthesis

8.7.1 General Aspects

In zeolite synthesis, silicate and aluminate ions are reacted with base under hydrothermal conditions. Basic components such as inorganic alkali or alkaline earth metal cations can also be used in the synthesis, in addition to organic cations. The organic cations can act as a structure-directing template.

The Al/Si ratio of the zeolite framework and the structure of zeolite are quite sensitive

Self Organization and Self Assembly of Catalytic Systems 355

to the base cation used in the synthesis. The use of organic templates tends to decrease the Al/Si ratio in the zeolite. Their bulkiness restricts the number of cationic template molecules adsorbed per unit micropore surface area and, hence, the compensating negative charge density on the micropore zeolite wall that relates to the Al/Si ratio of the zeolite framework.

The interaction between template and zeolite lattice also controls to a significant extent the shape of the zeolite micropores and, hence, the zeolite structure. Similarly, to catalyst design of antibodies in response to a templating antigen, one can select the organic base template as an analogue of a transition state or key intermediate in the reaction sought to be catalyzed by the zeolite. In this way, the size and shape of the micropore that forms are selected to maximize interaction with the desired reaction intermediate. This will bias the reaction channels that pass through such intermediates. In zeolite formation a particular aluminosilicate cluster organizes around the template.

The zeolite synthesis solution provides a multitude of small oligomeric molecules that can display very di erent interactions with a selected template molecule. A specific complex with template molecule will have unique stability. Because of the equilibria between the oligomeric units, crystallization will consume all molecules from the mother liquid to form this particular complex through the recombination of particular oligomers formed.

Hence zeolite synthesis shares some of the same combinatorial self organization and self learning aspects as seen in the antibody system. During zeolite crystallization template molecules are incorporated in unique positions. Molecular mechanics techniques have been developed[26] that allow the prediction of optimum template zeolite interaction useful to select template molecules to synthesize preselected zeolite structures.

An interesting advance in the synthesis of reactant-directed solid-state catalysts that are not zeolitic is catalyst design of an alkene epoxidation catalyst[27]. They showed self

5−

assembly of a catalytic polyanion cluster α- (CoII)PW11O39 during catalysis from

components Co2+, H2PO−4 , WO4 2− and protons. The components themselves are not catalytically reactive. The catalytic activity increases with time until it saturates. Most likely the formation of the catalytically active cluster is catalyzed by the oxidized complex itself and we will deal with an example of autocatalysis.

8.7.2 Mechanism of Zeolite Synthesis

Zeolite synthesis occurs at temperatures between 100 and 200◦C in a basic medium under hydrothermal conditions. Usually high concentrations of silica and alumina sources are used and synthesis occurs from a state where initially a gel is formed. Upon heating, silicate and aluminate species dissolve from the gel and chemistry relevant to crystallization occurs in the solvent phase. Nucleation itself is assisted by nucleation sites o ered by the gel material.

The most detailed picture of zeolite synthesis available to us is for siliceous silicalite. We will discuss this here in an attempt to illustrate molecular recognition of template, evolutionary recombination of reaction intermediate oligomers and self replication. Detailed information became possible once homogeneous conditions for zeolite formation in silicate synthesis were found in the absence of gel formation. For a concise and excellent review on general mechanistic aspects of zeolite synthesis we refer to Cundy an Cox[37].

A basic silicate solution consists of a mixture of many di erent monomers, illustrated in Fig. 8.13. Monomers, dimers, trimers and higher oligomers are formed, in ratios that