
Kosevich A.M. The crystal lattice (2ed., Wiley, 2005)(ISBN 3527405089)(342s)_PSa_
.pdf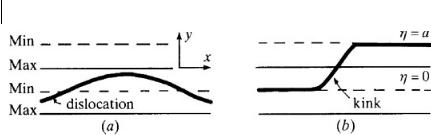
334 14 Dislocation Dynamics
Fig. 14.3 Two types of dislocation motion in the field of the Peierls potential: (a) the dislocation vibrates in one potential valley; (b) the dislocation forms a kink moving along the x-axis.
It is clear that (14.4.6) is an inhomogeneous sine-Gordon equation, so that its solitons are associated with the dislocation kinks.
Unfortunately, the local equation of motion for the dislocation element (14.4.6) cannot be derived consistently from the equation of motion (14.4.1). In a crystal there are no specific interactions decreasing so fast in space that it be possible to pass from the integral equation (14.4.1) to the differential equation in partial derivatives (14.4.6). The elastic stresses causing the interaction of various parts of the same dislocation decrease very slowly with distance, so that such dislocation parameters as the mass m per unit length or the linear tension coefficient TD are not local characteristics of the dislocation. Although the string model is limited, it is often used to demonstrate the physical phenomena generated by the dislocation bending vibrations. The model is attractive primarily because it is simple and enables good results to be obtained. However, the conclusions made from an analysis of (14.4.6) need to be re-examined.
We shall take the r.h.s. of (14.4.6) as an external force. In the absence of an external field (σ = 0), then the dislocation motion has the character of free oscillations corresponding to the normal modes of string vibrations and having the dispersion law
|
ω2 = ω02 + c02 k2, |
|
(14.4.7) |
|
where |
|
|
|
|
ω2 |
= 2πbσ /(ma), |
c2 |
= T /m. |
(14.4.8) |
0 |
P |
0 |
D |
|
Let us discuss the dispersion law (14.4.7). In analyzing the waves localized near the dislocation (Section 12.2) it was noticed that its bending vibrations should have a propagation velocity that does not actually differ from that of transverse sound vibrations st. To confirm this conclusion with (14.4.7) we assume c0 = st, which does not contradict the estimates (14.3.7), (14.3.8). But the dispersion law frequencies (14.4.7) satisfy the inequality
ω > c0k = stk. |
(14.4.9) |
The wave running along the dislocation with wave vector k and frequency (14.4.8) cannot be localized near the dislocation because it inevitably excites bulk vibrations whose frequencies satisfy the same condition (14.4.9). Thus, the string vibration with

14.4 Equation for Dislocation Motion 335
the dispersion law (14.4.7), if it exists, has the character of a quasi-local vibration. Unfortunately, it cannot be pronounced. Indeed, it is easily seen that the connection of the dislocation line vibrations with the vibrations of crystal lattice atoms is characterized by the same parameter that determines the eigenfrequency ω0.
We note that the periodic potential in whose valleys the dislocation vibrates is created by the crystal atoms. Thus, it is more natural in (14.4.6) to write the periodic term in a different way, i. e.,
∂2 η |
2 ∂2 η |
+ |
aω02 |
η − uy |
= 0, |
|
||
∂t2 |
− c0 |
∂x2 |
2π |
sin 2π |
a |
(14.4.10) |
||
where uy is the long-wave atomic displacement in the vicinity of the dislocation core. In studying small vibrations, we have instead of (14.4.10)
∂2 η |
2 |
∂2 η |
2 |
2 |
|
|
− c0 |
|
+ ω0 |
η = ω0 uy, |
(14.4.11) |
∂t2 |
∂x2 |
where there is no small coupling parameter between the dislocation and sound displacements that permits consideration of free dislocation vibrations in the valley of a periodic potential relief.
Thus, examining the eigenvibrations of a dislocation-string leads to the conclusion that (14.4.6) is not a satisfactory model for describing the motion of a free dislocation.
However, this model is quite applicable for investigating the dislocation vibrations under the action of an oscillating external force. We consider the dislocation vibrations under the conditions when the Peierls forces can be neglected (e. g., at high temperatures) and the retarding force of the dislocation that is proportional to its velocity becomes important. In this case the dislocation motion obeys an equation similar to (14.4.6), but the term appearing from the Peierls potential can be omitted and the dissipative term B(∂η/∂t), where B is the multiplier depending on the nature of dissipative forces, is added. As a result we get
m |
∂2 η |
+ B |
∂η |
− |
T |
∂2 η |
= bσ e−iω t. |
(14.4.12) |
∂t2 |
∂t |
|
||||||
|
|
D ∂x2 |
0 |
|
||||
We assume that the dislocation is fixed at the two points ±l/2. This fixing can be produced by a strong interaction of the dislocation core with a poorly mobile impurity in a crystal. Then, the solution for the forced vibrations of a dislocation segment is the function
η = |
bσ0 e−iω t |
|
cos kx |
− 1 , |
(14.4.13) |
k2 TD |
|
cos 1 kl |
|||
|
|
2 |
|
|
|
where k2 = (mω2 + iBω)/TD.
Equation (14.4.12) and its solution (14.4.13) are the basis for a dislocation theory of internal friction worked out in detail by Granato and Lucke (1956).

33614 Dislocation Dynamics
14.5
Vibrations of a Lattice of Screw Dislocations
Consider a superstructure formed by a lattice of parallel screw dislocations. By dislocation lattice we mean a system of parallel screw dislocations oriented along the z-axis
and intersecting the xy plane at discrete periodically arranged points, forming a 2D lattice, the unit cell of which has area S0: S = NS0, where S is the cross-sectional area of the sample in the xy plane and N is the number of dislocations. The coordinates of
these points in the equilibrium lattice are
x(n) = Rn + ∑dα nα , |
|
n = (n1, n2, 0), |
(14.5.1) |
n |
|
|
|
where dα (α = 1, 2) are the basic translation vectors of the lattice (dα |
d is the |
||
distance between neighboring dislocations: S |
0 |
= d2). |
|
|
|
|
|
We intend to use a simple one-component scalar model of vibrations in which it is assumed that all the atoms are displaced only in one direction. The basis of using such a model is the fact that a static screw dislocation in the isotropic media produces the scalar field of displacements w along the z-axis. The model gives a correct description of the elastic field created in an isotropic medium by parallel screw dislocations. The solution of such a problem in a real vector displacement scheme can in principle be found analytically, but it permits obtaining the dispersion relation of the dislocation lattice only in implicit form. For the sake of simplicity we restrict ourselves to the scalar model.
If there are rectilinear screw dislocations directed along the z axisx, then the elastic field is more conveniently described not by the displacement w along the z-axis but by the distortion and velocity of the displacements as functions of the coordinate and time. Following (13.1.10) and (13.1.12), for describing the shear field of screw dislocations we introduce a distortion vector h and a stress vector σ = Gh (G is the shear
modulus): |
∂w |
|
|
|
h = grad w, hi = i w = |
, i = 1, 2, 3, |
(14.5.2) |
||
|
||||
∂xi |
||||
and a velocity v: v = ∂w/∂t. Equation (13.1.11) conserves its form |
|
|||
curl h = −α, |
|
(14.5.3) |
||
and the density of dislocations α is equal to |
|
|
|
|
α = τb ∑δ(x − Rn ),
n
where b is the modulus of the Burgers vector and τ is the tangent vector to the dislocation; for a static dislocation it is conveniently chosen as τ(0, 0, −1).
The wave equation for the elastic field in the medium between dislocations takes the usual form (14.3.1):
1 ∂v |
= 0 . |
|
div h − s2 ∂t |
(14.5.4) |

14.5 Vibrations of a Lattice of Screw Dislocations 337
If the dislocations move (vibrate), then (14.5.3), (14.5.4) do not change, but a new variable of the dislocation structure appears: u = (ux, uy, 0) (of course, u = u(n, t) for the n-th dislocation), which determines the instantaneous coordinate of an element
of the dislocation:
xn = R(n) + u(n, t) .
The time dependence of the displacement vector u gives the velocity V of an element of the dislocation (Vα = ∂u/∂t) that generates a dislocation flux. The dislocation flux density vector j arises in the dynamical equation (14.1.3):
∂h |
= grad v + j . |
(14.5.5) |
|
∂t |
|||
|
|
In the case under consideration the flux density is given by the formula following from (14.1.4):
jα = bε αβ ∑Vβ (n)δ (x − R(n)) , α = 1, 2 , |
(14.5.6) |
n |
|
where the matrix ε αβ
0 |
1 |
|
ε αβ = |
. |
(14.5.7) |
−1 |
0 |
|
Collecting together (14.5.3)–(14.5.5) we obtain the total set of equations describing the elastic field in the sample if the distribution of dislocations and their fluxes are known. To close this system it is necessary to write equations of motion for the dislocations under the influence of the elastic fields. The simplest form of such an equation can be obtained using (14.4.1) and (14.4.4) for rectilinear dislocations:
m |
∂Vα |
= fα + Sα , α = 1, 2 , |
(14.5.8) |
|
|||
|
∂t |
|
|
here m is the effective mass of a unit length of the dislocation (with the order of magnitude (14.3.7), where R is the distance between dislocations in our case), and f is equal to
fα = bε αβ σβ = bGε αβ hβ . |
(14.5.9) |
In the case of a curved dislocation line expression (14.5.9) includes the self-force from different elements of the same dislocation, which is proportional to the curvature of the dislocation line at the given point. In the analysis of small vibrations the curvature of the dislocations can not be taken into account, and the force (14.5.9) includes only the stresses created by the other dislocations.
Usually S is the force due to the discreteness of the lattice, including dissipative forces. As we are interested in the dispersion relation for small vibrations, we neglect the latter and take the force in the form equivalent to that on (14.4.11), namely,
S = −mω02u, |
(14.5.10) |


14.5 Vibrations of a Lattice of Screw Dislocations 339
vibrations. Thus one branch of collective vibrations (we call it the branch of “longitudinal” vibrations) corresponds to independent oscillations of the elastic filed v= v(z, t) with the dispersion relation ω = skz and to compression–rarefaction oscillations of the dislocation lattice P = P(z, t) with the dispersion relation ω = ωl.
To describe to “transverse” vibrations we introduce the variable
M = bn0 (curl V )z = bn0 ε αβ α Vβ . |
(14.5.17) |
The equation for this variable follows from (14.5.13):
∂2 M |
2 |
2 ∂2 v |
|
||
|
+ ωl |
M = −ω pl |
|
. |
(14.5.18) |
∂t2 |
∂x2 |
||||
|
|
|
α |
|
|
The “transverse” collective vibrations are described by (14.5.18) and the following equation obtained from (14.5.15) for the function v(x, y, t):
1 ∂2 |
∂2 |
|
||||
|
|
|
− |
|
v = M. |
(14.5.19) |
s2 |
∂t2 |
∂xα2 |
||||
The compatibility conditions for (14.5.18) and (14.5.19) give the dispersion relation for a wave with wave vector k(kx, ky, 0):
ω4 − (ωl2 + s2 k2 )ω2 − ω02s2 k2 = 0. |
(14.5.20) |
Equation (14.5.20) has two roots for ω2, which correspond to low-frequency and high-frequency oscillations. Without writing the trivial expressions for these solutions in quadratures, we note the following:
Low-frequency branch. For sk ω0 the dispersion relation has the form
ω = |
ω0 |
sk. |
(14.5.21) |
|
ωl |
||||
|
|
|
The vibrations are characterized by a transverse sound velocity, the value of which is less than the sound velocity s in the medium without the dislocations.
High-frequency branch. For sk ωl the inertial dislocation lattice is not entrained in the motion, and one observes only vibrations of the elastic field with the usual sound dispersion relation ω = sk. Finally, in the long-wavelength limit (sk ω0) we obtain
ω2 = ωl2 + |
ω pl |
s2 (k2x + k2y). |
(14.5.22) |
|
ωl |
||||
|
|
|
In comparing the graphs of the two branches of the dispersion relation, one must be particularly careful in rendering the low-frequency branch. The point is that dispersion relation (14.5.20) is valid for λ a (or ak 1). At large k the dispersion relation of the lattice manifests a periodic dependence on the quasi-wave vector with the reciprocal lattice period G: ω(k) = ω(k + G). Therefore the dispersion relation obtained is actually valid in all small neighborhoods of any 2D reciprocal lattice
340 14 Dislocation Dynamics
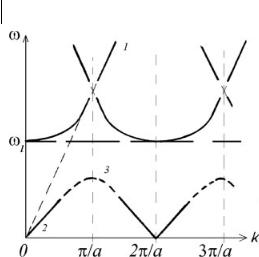
Fig. 14.4 Diagram of the dispersion relation : (1) ω = sk, (2) plot of (14.5.21), (3) expected form of the graph in the short-wavelength region.
vector g, i. e., for a |k − g| 1. Consequently, we are justified in drawing only the part of the graphs shown by the heavy solid lines 1 and 2 in Fig. 14.4 for a certain “good” direction in the reciprocal lattice. The continuation of the graph of the lower branch at k π/a and also the indicated crossing of the graphs of the upper branch at k = ( p + 1/2)π/a, p = 1, 2, 3, . . . can be described only on the basis of a study of the dynamics of the discrete dislocation lattice. That is a subject for a separate study. We can only state that the graph of the lower branch is closed by the curves illustrated schematically by the dotted lines 3 in Fig. 14.4. Whether or not there is a band of forbidden frequencies between the upper and lower branches (gap in the spectrum) one cannot say on the basis of a long-wavelength treatment. However, one can say that the frequency spectrum has a limiting frequency ωl that marks the edge of the upper branch of vibrations, which can certainly be manifested in the acoustic resonance properties of a crystal with a dislocation lattice.
Bibliography
Andreev A.F., Lifshits I.M., Zh. Eksper. Teor. Fiz. 56, 2057 (1969) (in Russian). Berezinsky V.L., Zh. Eksper. Teor. Fiz. 61, 1144 (1971) (in Russian).
de Boer J., Physica 14, 139 (1948).
Brout R., Visher W., Phys. Rev. Lett. 9, 54 (1962).
Chebotarev L.V., private communication (1980).
Chou Y.T., Acta Metall. 13, 251 (1965).
Debye P., Ann. Phys. 43, 49 (1914).
Dzyub I.P., Fiz. Tverd. Tela 6, 3691 (1964) (in Russian).
Goldstone J., Nuovo Cimento 19, 154 (1961).
Granato A., Lucke K.J., Appl. Phys. 27, 789 (1956).
Ivanov M.A., Fiz. Tverd. Tela 12, 1895 (1970) (in Russian).
Kagan Yu., Iosilevskii Ya., Zh. Eksper. Teor. Fiz. 42, 259 (1962); 44, 284 (1963) (in Russian).
Kontorova T.A., Frenkel Ya.I., Zh. Eksper. Teor. Fiz. 8, 80 (1938); 8, 1340 (1938) (in Russian).
Kosevich A.M., Zh. Eksper. Teor. Fiz. 43, 637 (1962) (in Russian); Soviet Phys. – JETP (English Transl.) 16, 455 (1963).
Kosevich A.M., Pis’ma Zh. Eksper. Teor. Fiz. 1, 42 (1965) (in Russian). Kosevich A.M., Khokhlov V.I., Fiz. Tverd. Tela 12, 2507 (1970) (in Russian). Kosterlitz J.M., Thouless D.J., J. Phys. C6, 1181 (1973).
The Crystal Lattice: Phonons, Solitons, Dislocations, Superlattices, Second Edition. Arnold M. Kosevich Copyright c 2005 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim
ISBN: 3-527-40508-9

342 Bibliography
Kroener E., Rieder G., Z. Phys. 145, 424 (1956).
Lifshits I.M., Zh. Eksper. Teor. Fiz. 17, 1076 (1947) (in Russian).
Lifshits I.M., Zh. Eksper. Teor. Fiz. 22, 475 (1952) (in Russian).
Lifshits I.M., Usp. Fiz. Nauk 83, 617 (1964) (in Russian).
Lifshits I.M., Kosevich A.M., Rep. Progr. Phys. 29, pt. 1, 217 (1966).
Lifshits I.M., Peresada V.I., Uchen. Zapiski Khark. Univers. Fiz.-Mat. Fakult. 6, 37 (1955).
Mura T., Philos. Mag. 8, 843 (1963).
Nabarro F.R.N., Proc. Phys. Soc. A 59, 256 (1947).
Nicklow H.G., Wakabayashi N., Smith H.G., Phys. Rev. B 5, 4951 (1972). Ott H., Ann. Phys. 23, 169 (1935).
Peach M.O., Koehler J.S., Phys. Rev. 80, 436 (1950).
Peierls R.E., Proc. Roy. Soc. 52, 34 (1940).
Pushkarov D.I., Zh. Eksper. Teor. Fiz. 64, 634 (1973) (in Russian); Soviet Phys. – JETP (English Transl.) 37(2), 322 (1973).
Rytov S.M., Akust. Zhurn. (in Russian) 2, 71 (1956).
Slutskin A.A., Sergeeva G.G., Zh. Eksper. Teor. Fiz. 50, 1649 (1966) (in Russian). Walker C.B., Phys. Rev. 103, 547 (1956).
Waller I., Dissertation, Uppsala (1925).
Warren J.L., Wenzel R.G., Yarnell J.L., Inelastic Scattering of Neutrons (IAEA, Viena, 1965).
Weertman J., Philos. Mag. 11, 1217 (1965).
Woods A.D.B., Cochran W., Brockhouse B.N., Cowley R.A., Phys. Rev. 131, 1025 (1963).
Yarnell J.L., Warren J.L., Koenig S.H., in: Lattice Dynamics (Pergamon Press, Oxford, 1965), p. 57.
Zinken A., Buchenau U., Fenzl H.J., Schrober H.R., Solid State Commun. 22, 693 (1977).
