
Теоретическая часть.
 Несовершенная
скважина радиусом
Несовершенная
скважина радиусом ![]() вскрывает пласт на всю толщину, Радиус
контура питания
вскрывает пласт на всю толщину, Радиус
контура питания ![]() .
Имеется плоский фильтрационный поток.
Расчетная схема представлена на рисунке
1.
.
Имеется плоский фильтрационный поток.
Расчетная схема представлена на рисунке
1.

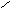
 y
M
y
M




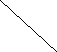

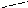

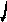
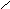
![]()
![]()
![]()
![]()



![]()









 -q
A´
-q
A´
![]()
![]() A
+q
x
A
+q
x


Рисунок 1 - Расчетная схема.
Для
решения используем метод отображения
источников и стоков. Зеркально отобразим
скважину-сток А относительно прямолинейной
непроницаемой границы скважиной-стоком
А´ равного дебита. Расстояние от скважин
до прямолинейной непроницаемой границы
равно ![]() ,
а до контура питания равно
,
а до контура питания равно ![]() .
.
Дебит скважины, приходящийся на единицу толщины пласта:

![]() приведенный
радиус скважины;
приведенный
радиус скважины;
![]() потенциал
на контуре питания;
потенциал
на контуре питания;
![]() потенциал
на забое скважины.
потенциал
на забое скважины.
Связь потенциала с давлением:
![]()
![]()
![]()
Приведенный радиус скважины:
![]()
![]() дополнительное
фильтрационное сопротивление, вызванное
несовершенством по характеру вскрытия
пласта.
дополнительное
фильтрационное сопротивление, вызванное
несовершенством по характеру вскрытия
пласта.
Коэффициент
C
определяем по графикам Щурова ![]() .
.
![]()
По
графикам на рисунках 4.20 (стр. 67 ![]() )
определяем C:
)
определяем C:
![]()
![]()
Потенциал в любой точке пласта:
![]()
![]() расстояние
от реальной скважины А;
расстояние
от реальной скважины А;
![]() расстояние
от фиктивной скважины А´.
расстояние
от фиктивной скважины А´.
Для
точек на оси x:
![]()
![]() .
.
Дебит скважины:
![]()
Коэффициент продуктивности:
![]()
Скорость фильтрации в любой точке пласта:
![]()
![]() скорость
фильтрации реальной скважины А, направлена
к скважине А;
скорость
фильтрации реальной скважины А, направлена
к скважине А;
![]() скорость
фильтрации фиктивной скважины А´,
направлена к скважине А´.
скорость
фильтрации фиктивной скважины А´,
направлена к скважине А´.
Скорость фильтрации в отверстиях:
![]()
Скорость движения частиц жидкости:
![]()
Чтобы установить закон фильтрации, определим число Рейнольдса по формуле Щелкачева:
![]()
![]()
![]() коэффициент
кинематической вязкости жидкости.
коэффициент
кинематической вязкости жидкости.
![]()
Время движения частиц жидкости:
![]()
![]() расстояние;
расстояние;
![]() скорость
частиц жидкости.
скорость
частиц жидкости.
Уравнение эквипотенциалей соответственно для отрицательных и положительных значений x:
![]()
Уравнение линий тока:
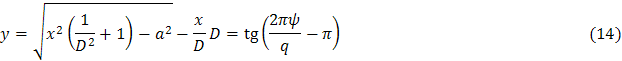
![]() функция
тока.
функция
тока.
