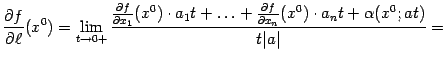ответы к билетам матан 1 семестр docx - 2010 / 37.Производная по направлению

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

Заметим, что если направление оси совпадает с направлением одной из координатных осей , то производная функции по такому направлению, очевидно, равняется (правой) производной функции по соответствующей переменной . Если существует (двусторонняя) частная производная по , то получаем, что

если .

Используя параметризацию точки на луче вида и замечая, что условие означает, что , получаем:

Запишем теперь приращение функции, стоящее в числителе, через частные производные с помощью формулы (8.1):

Отсюда

Здесь в правой части первые слагаемых не зависят от . Поскольку при , то последний предел равен 0, так как  -- величина большего порядка малости, чем . Итак, получили формулу

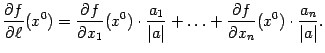
С помощью этой формулы можно вычислять производную по любому направлению, если известен направляющий вектор этого направления .