ответы к билетам матан 1 семестр docx - 2010 / 44.Интегральный признак Коши

Теорема 8. (Интегральный признак Коши)

Пусть члены знакоположительного числового ряда u₁+u₂+…+u_n… (7) не возрастают: u₁u₂≥…≥u_n≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, что f(1)=u₁, f(2)= u₂ ,…,        f(n)= =u_n,… . Тогда ряд (7) сходится или расходится одновременно с несобственным интегралом

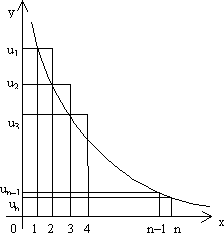
Доказательство. Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольник с основаниями [1;2], [2;3], …, [n-1;n] и высотами u₁,u₂,…,u_n-1, а также с высотами u₂,u₃,…,u_n.

S_n=u₁+u₂+…+u_n-1+u_n, S_впис=u₂^.1+u₃^.1+…+u_n^.1=u₂+u₃+…+u_n=S_n-u₁,

S_опис=u₁+u₂+…+ +u_n-1=S_n-u_n.

Площадь криволинейной трапеции S= . Получаем S_n-u₁< < S_n-u_n. Отсюда

S_n<u₁+          (17)

и S_n>u_n+       (18)

Пусть  сходится. Это означает, что существует конечный предел =Y. Соотношение (17) принимает вид: S_n<u₁+Y при любом n. Это означает, что последовательность частичных сумм S_n ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть  расходится. Это означает, что =∞ и тогда из (18) следует, что последовательность частичных сумм S_n ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.

2