ответы к билетам матан 1 семестр docx - 2010 / 41. Ряды Дирихле. Гармонический ряд

Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд^[1][3]

.

В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда^[1]:

.

Пример 1. Исследуем ряд Дирихле на сходимость в зависимости от р.

Решение. 1) В случае, если , члены ряда образуют неубывающую последовательность, а сам ряд расходится по необходимому признаку сходимости ().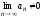

2) В случае для исследования сходимости ряда используем интегральный признак Коши. Введем функцию , которая удовлетворяет всем условиям теоремы Коши (теорема 3, лекция 1): при она непрерывна, положительна и монотонно убывает, . Вычислим несобственный интеграл в двух случаях а) , б) , т.е. когда :

а) Если , , 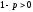то , тогда , следовательно, несобственный интеграл расходится и расходится исходный ряд.

б) Если , , то , тогда , следовательно, несобственный интеграл сходится и сходится исходный ряд.

3) В случае имеем гармонический ряд , для которого также применим интегральный признак Коши, т.е. рассмотрим интеграл , следовательно, несобственный интеграл расходится, а значит, гармонический ряд расходится.

Вывод: ряд Дирихле сходится, если , и расходится, если .