1.5. Интегральный признак Коши сходимости ряда с положительными членами
Теорема
3 (интегральный признак Коши).
Пусть дан ряд
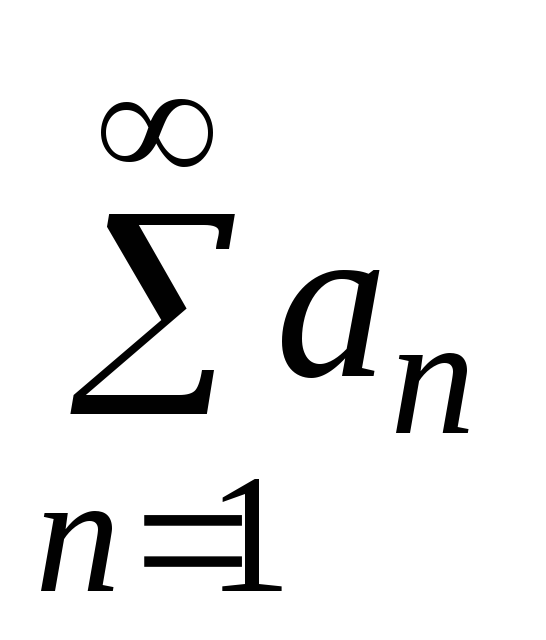 ,
члены которого удовлетворяют трем
условиям: а)
,
члены которого удовлетворяют трем
условиям: а)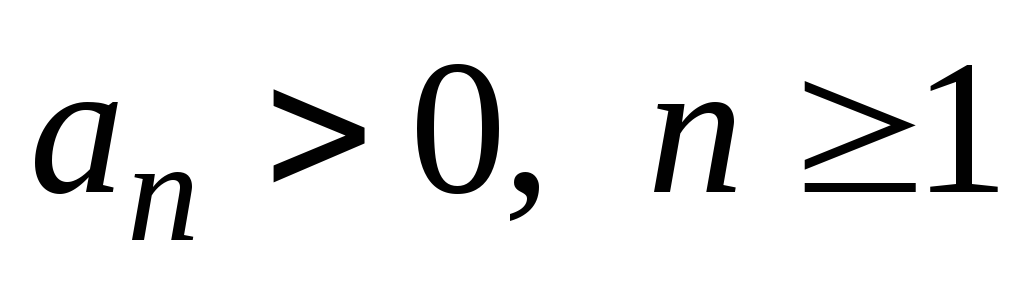 ,
т.е. исходный ряд с положительными
членами; б) члены ряда монотонно убывают,
т.е.
,
т.е. исходный ряд с положительными
членами; б) члены ряда монотонно убывают,
т.е.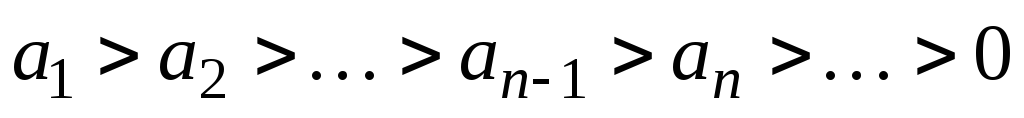 и в) общий член ряда стремится к нулю:
и в) общий член ряда стремится к нулю: .
Пусть существует непрерывная, монотонно
убывающая, определенная при
.
Пусть существует непрерывная, монотонно
убывающая, определенная при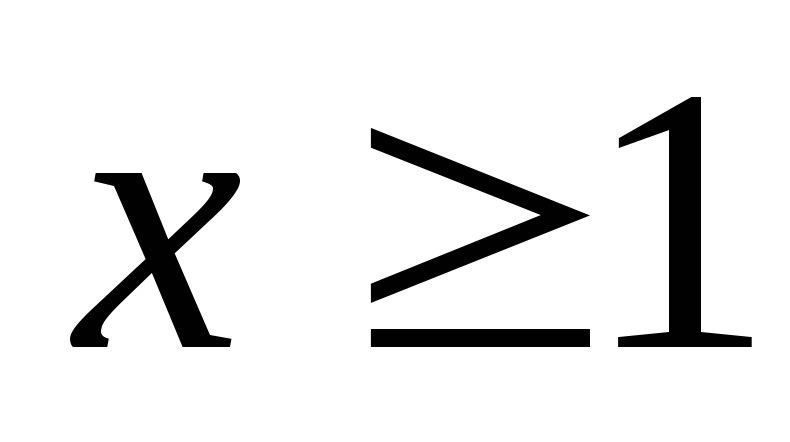 функцияf(x)
такая, что
функцияf(x)
такая, что
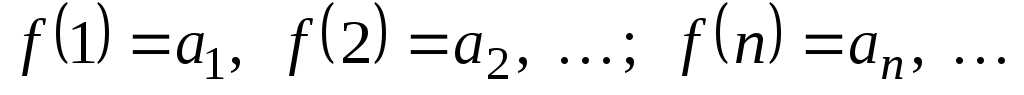 ,
т.е.
,
т.е.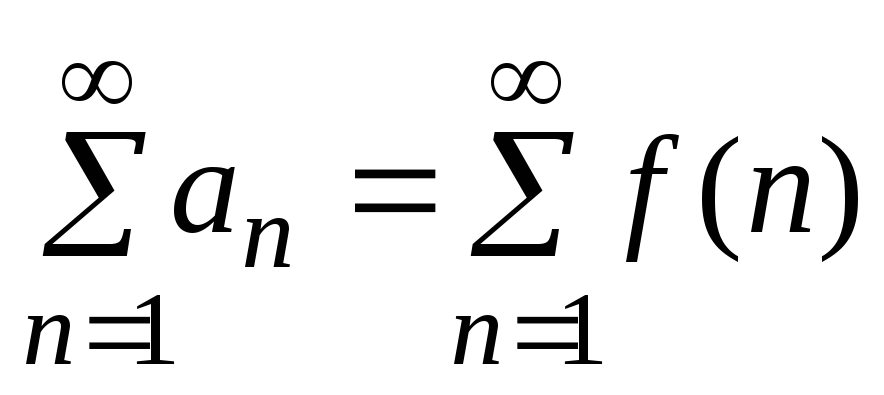 .
Тогда, если несобственный интеграл
.
Тогда, если несобственный интеграл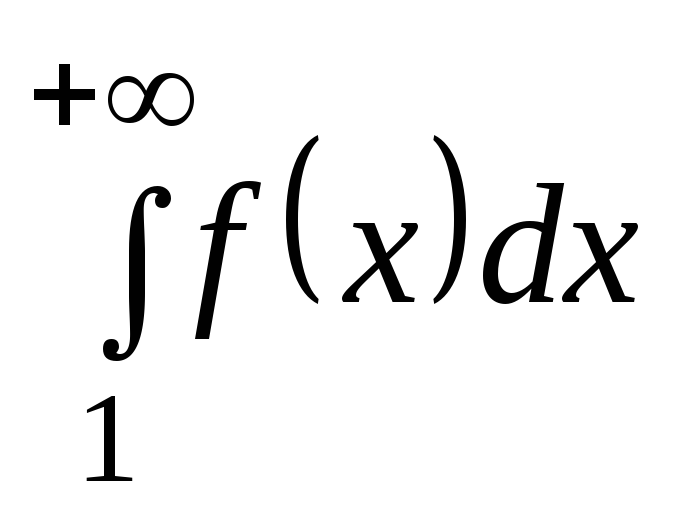 сходится, то ряд
сходится, то ряд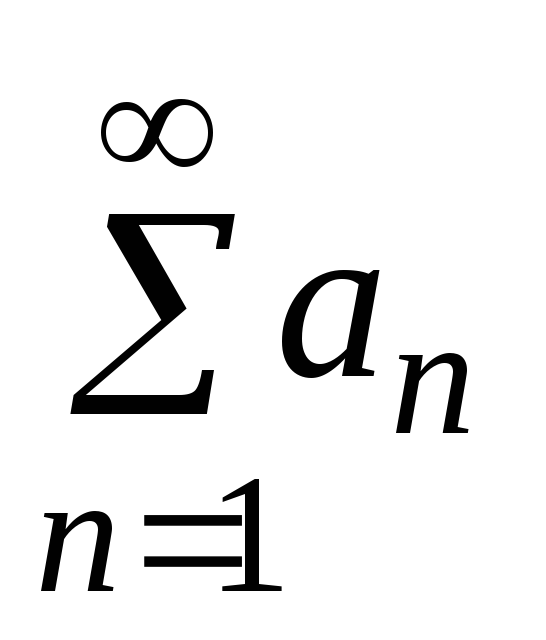 тоже сходится; если указанный интеграл
расходится, то этот ряд расходится.
тоже сходится; если указанный интеграл
расходится, то этот ряд расходится.
Доказательство.
Из условий теоремы
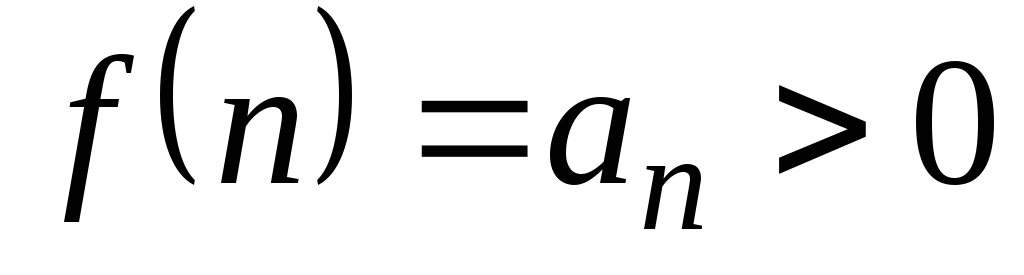 следует
следует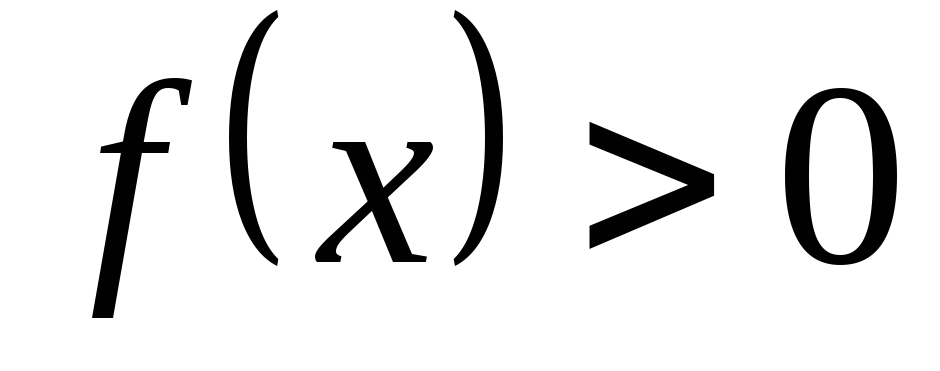 при
при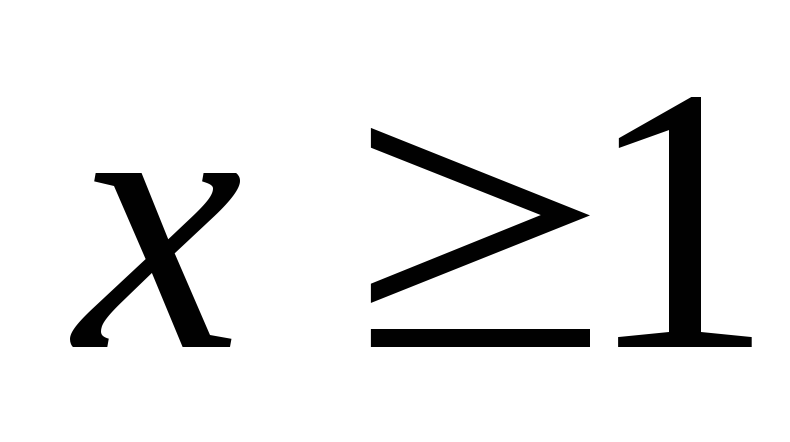 .
Рассмотрим криволинейную трапецию,
ограниченную линиями
.
Рассмотрим криволинейную трапецию,
ограниченную линиями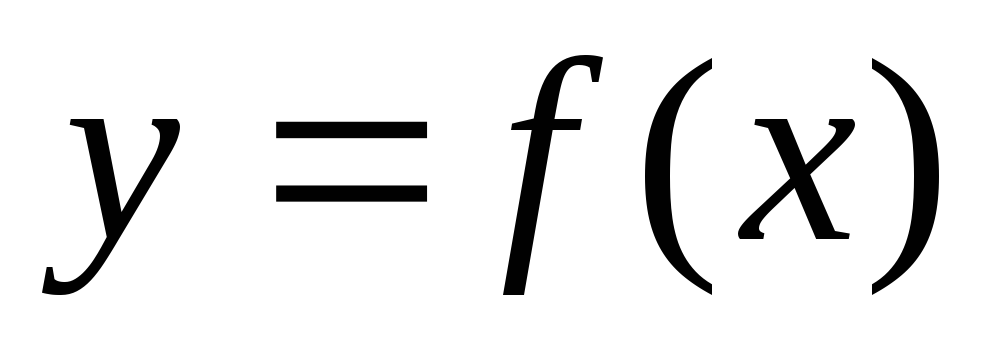 ,
,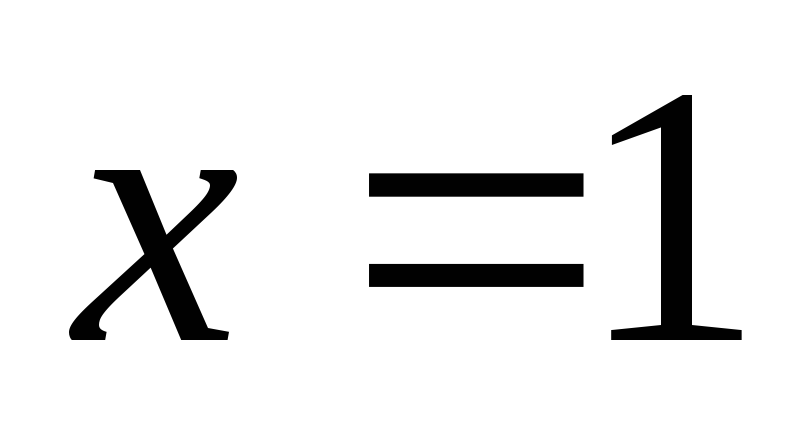 ,
,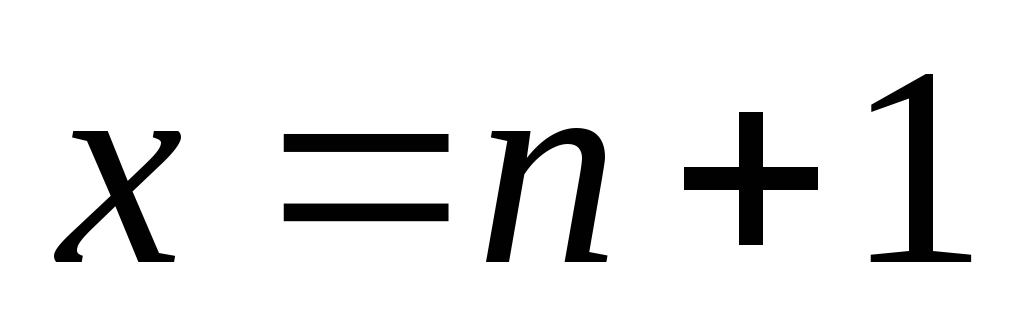 ,
осью 0х.
Разобьем отрезок
,
осью 0х.
Разобьем отрезок
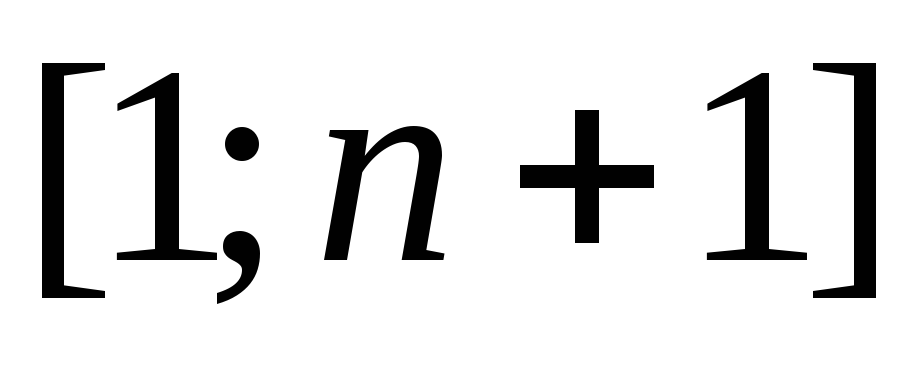 точками
точками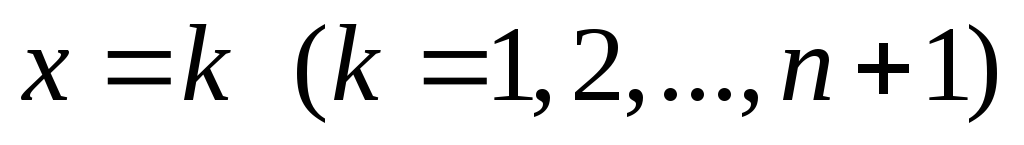 и рассмотримn
криволинейных трапеций.
и рассмотримn
криволинейных трапеций.
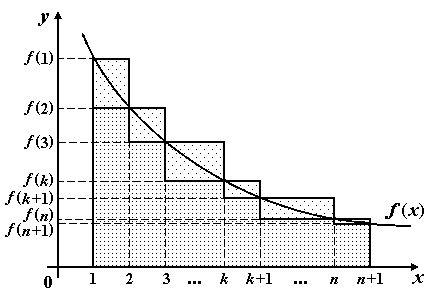
Рис.
1.
Из
геометрического смысла интеграла
площадь криволинейной трапеции
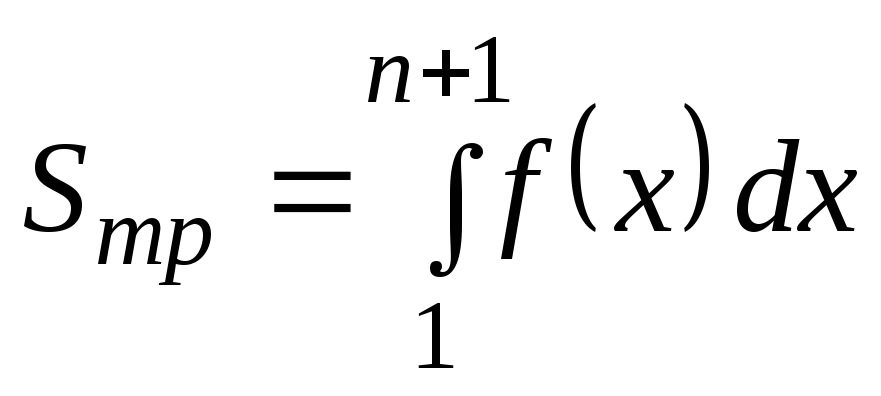 .
Заменим эту площадь суммой площадейn
прямоугольников с единичными основаниями:
.
Заменим эту площадь суммой площадейn
прямоугольников с единичными основаниями:
 ,
,
 ,
причем
,
причем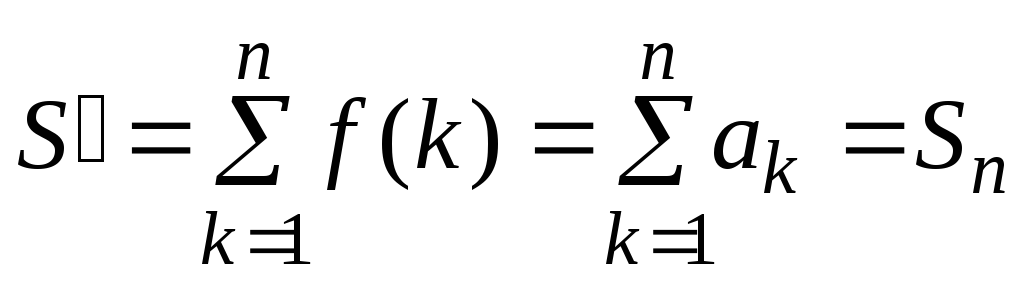 ,
а
,
а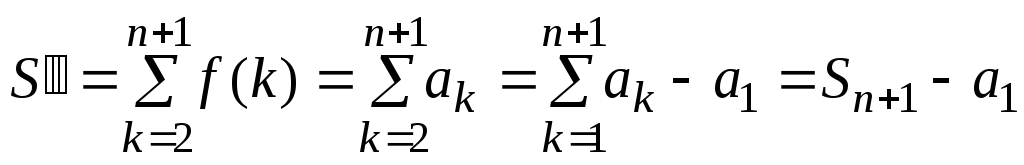 .
.
Из
графика (рис. 1) следует:
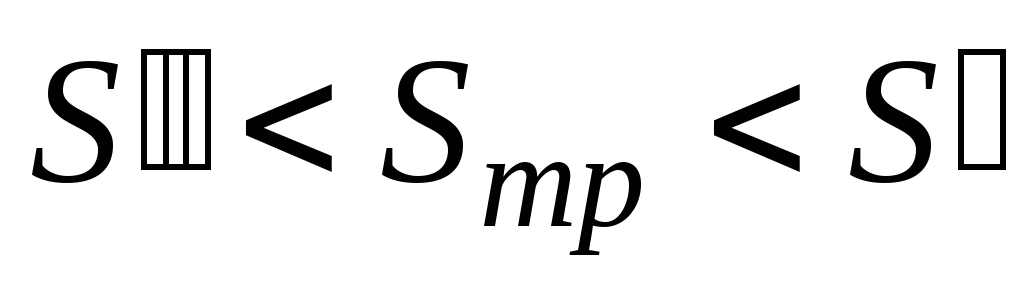 ,
т.е.
,
т.е.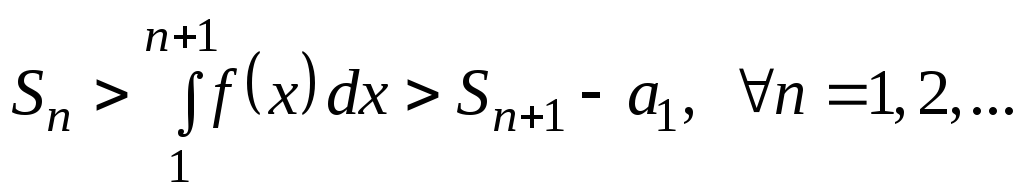 .
.
Рассмотрим
два случая. 1) Пусть
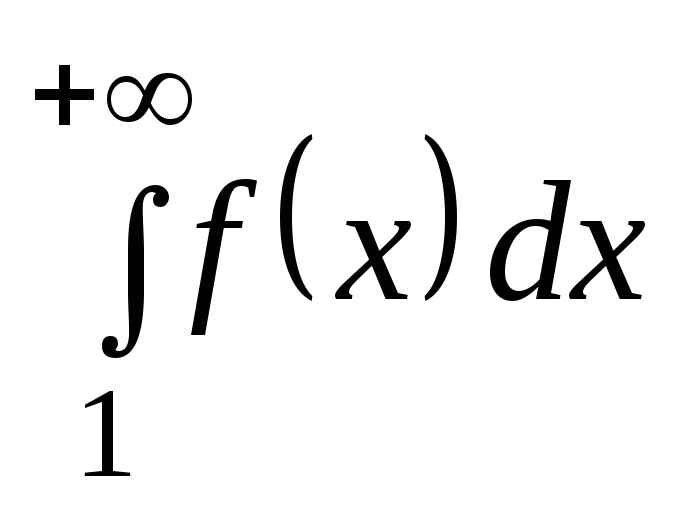 сходится (т.е. имеет конечный предел
сходится (т.е. имеет конечный предел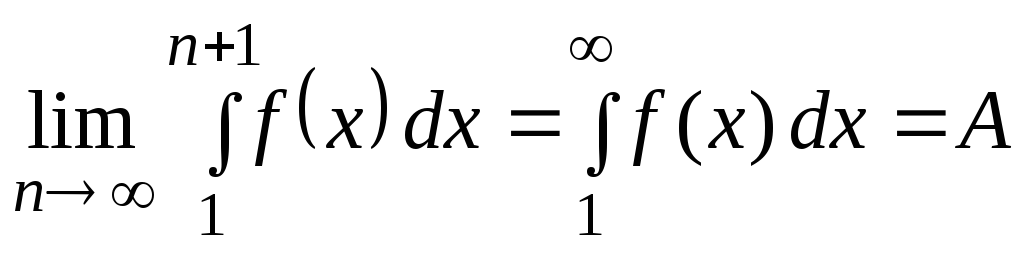 ).
Т.к.
).
Т.к.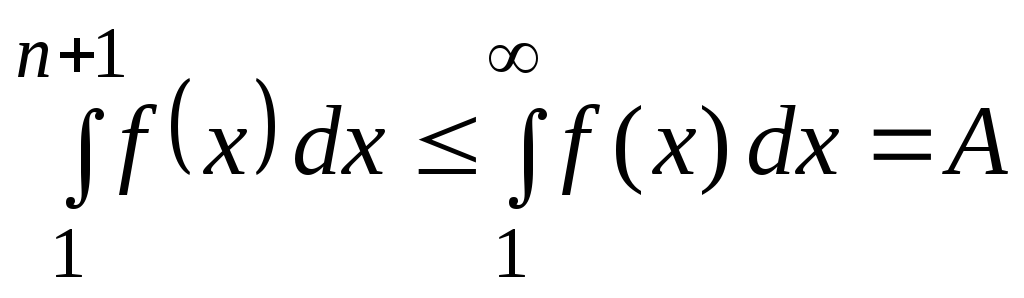 ,
то
,
то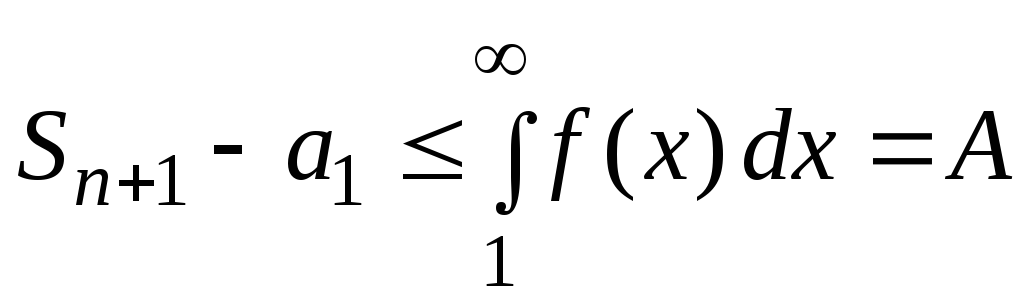 и
и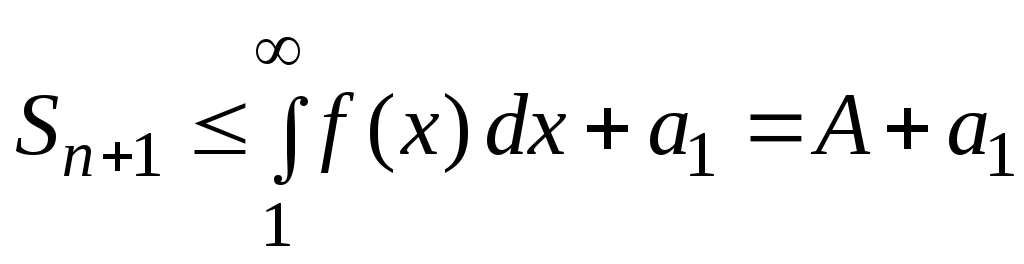 .
.
Итак,
частичные суммы ряда ограничены
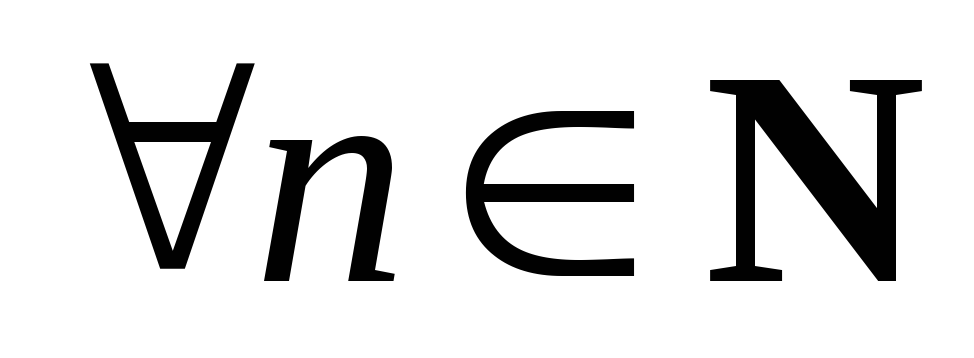 ,
тогда по теореме 2 (необходимый и
достаточный признак сходимости ряда с
положительными членами) ряд
,
тогда по теореме 2 (необходимый и
достаточный признак сходимости ряда с
положительными членами) ряд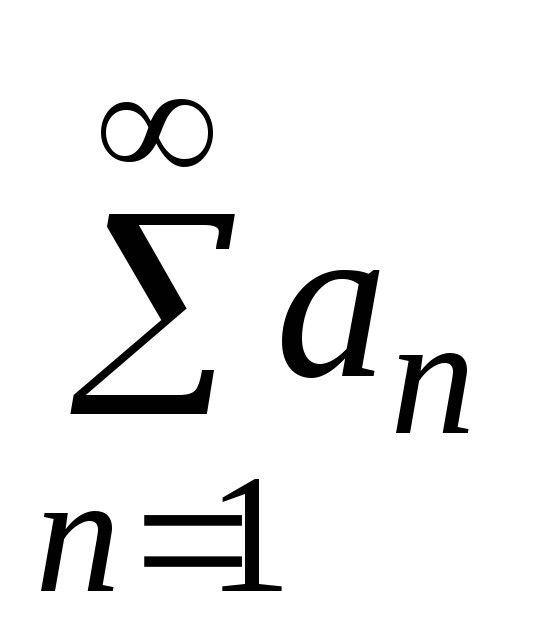 сходится, значит, существует
сходится, значит, существует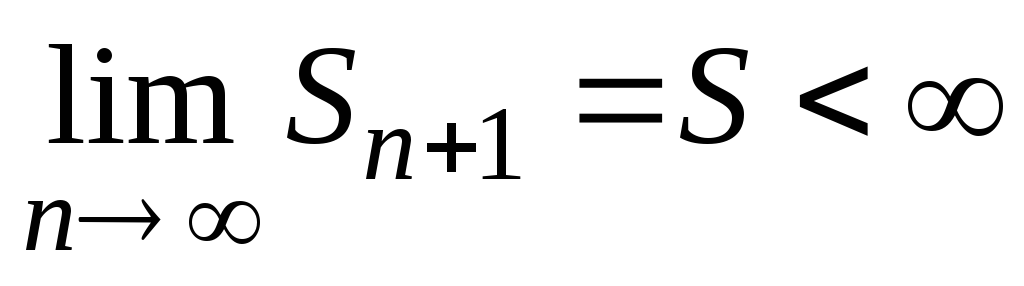 .
.
2)
Пусть интеграл
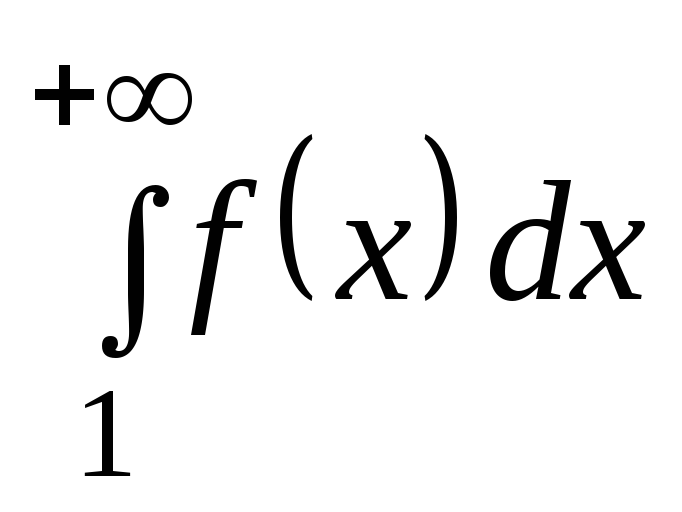 расходится, т.е.
расходится, т.е.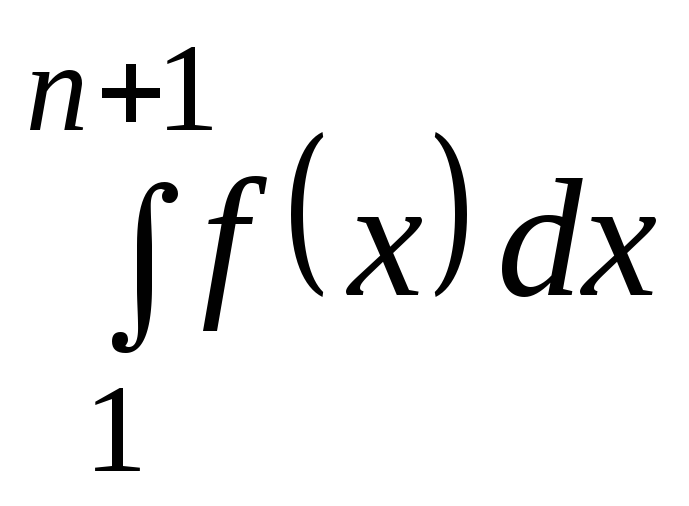 )
неограниченно возрастает при
)
неограниченно возрастает при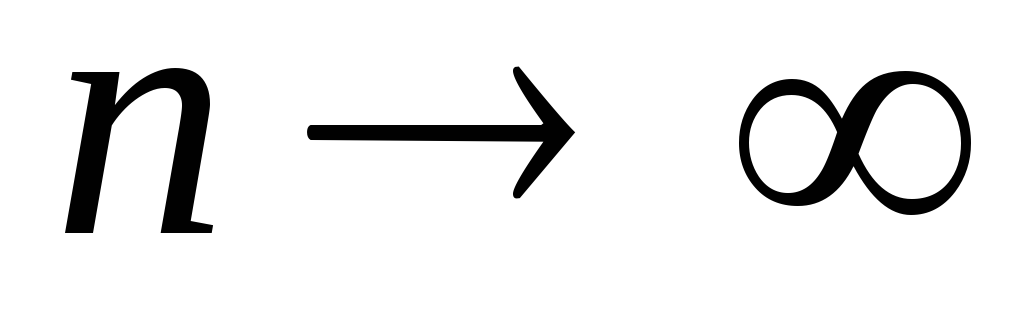 ,
тогда из неравенства
,
тогда из неравенства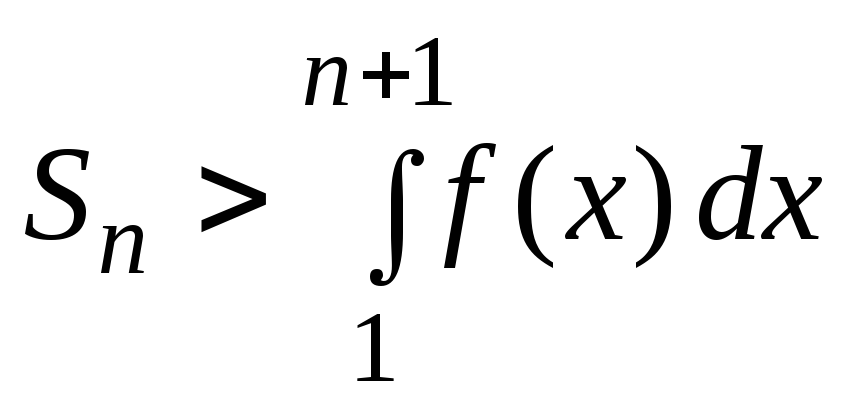 следует, что последовательность
следует, что последовательность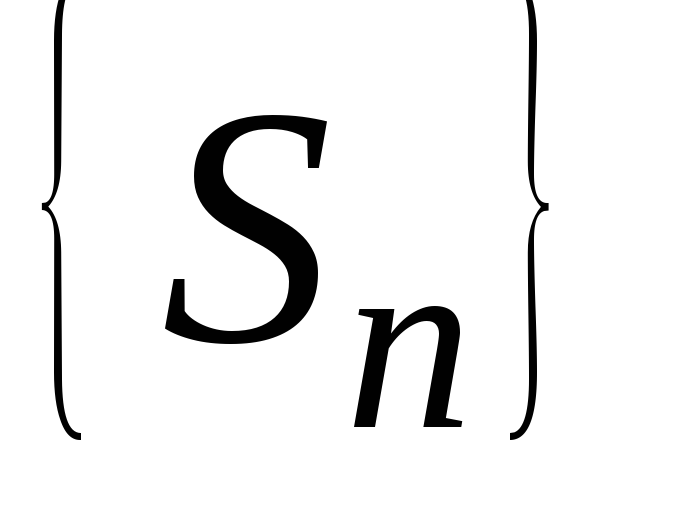 неограниченно возрастает:
неограниченно возрастает: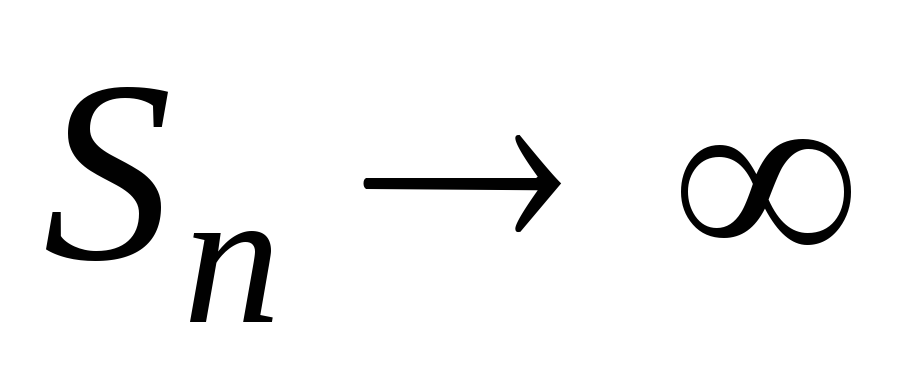 ,
т.е. ряд расходится. Теорема доказана.
,
т.е. ряд расходится. Теорема доказана.
Замечание
1.
Теорема остается верной и тогда, когда
ее условия выполняются не для всех
членов ряда, а лишь начиная с k-го
(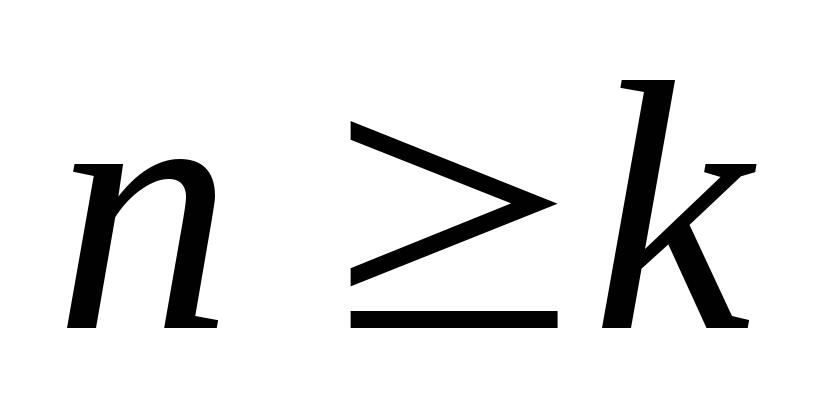 ),
в таком случае рассматривается интеграл
),
в таком случае рассматривается интеграл .Замечание
2.
Интегральный признак Коши существенно
облегчает исследование сходимости
ряда, т.к. позволяет свести этот вопрос
к выяснению сходимости интеграла от
удачно подобранной соответствующей
функции
.Замечание
2.
Интегральный признак Коши существенно
облегчает исследование сходимости
ряда, т.к. позволяет свести этот вопрос
к выяснению сходимости интеграла от
удачно подобранной соответствующей
функции
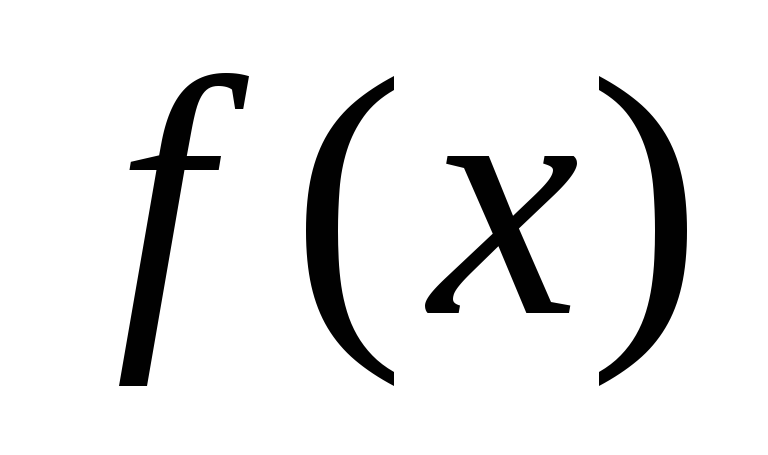 ,
что легко выполняется, применяя
рассмотренный ранее аппарат интегрального
исчисления.
,
что легко выполняется, применяя
рассмотренный ранее аппарат интегрального
исчисления.
7


