Матан - ряды - 2010

Раздаточный материал по теме «Ряды»

Выражение вида

,

где - члены ряда;  - n-ый или общий член ряда, называется бесконечным рядом (рядом).

Если члены ряда :

• числа, то ряд называется числовым;

• числа одного знака, то ряд называется знакопостоянным;

• числа разных знаков, то ряд называется знакопеременным;

• положительные числа, то ряд называется знакоположительным;

• числа, знаки которых строго чередуются, то ряд называется знакочередующимся;

• функции, то ряд называется функциональным;

• степени х, то ряд называется степенным;

• тригонометрические функции, то ряд называется тригонометрическим.

I. Числовые ряды. Ряды с положительными членами.

1.1. Основные понятия числового ряда.

Числовым рядом называется сумма вида

, (1.1)

где  называемые членами ряда, образуют бесконечную последовательность; членназывается общим членом ряда.

Суммы

…………..

,

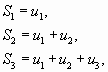
составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм .

Если при бесконечном возрастании номера n частичная сумма ряда   стремится к пределу S, то ряд называется сходящимся, а число S- суммой сходящегося ряда, т.е.

 и .

Эта запись равносильна записи

.

Если частичная сумма  ряда (1.1) при неограниченном возрастании n не имеет конечного предела (стремится к  или ), то такой ряд называется расходящимся.

Задание 1. Найти общий член числового ряда:

1. 2. 3. 4. 5.

6. 7. 8. 9. 10.

1.2 Необходимый признак сходимости ряда

Ряд  может сходиться только при условии, что его общий член  при неограниченном увеличении номера n стремится к нулю: .

Если  , то ряд   расходится – это достаточный признак расходимости ряда.

Задание 2.Проверить выполнение необходимого условия сходимости ряда:

11. 12. 13. 14. 15.

16. 17. 18. 19. 20.

1.3 Достаточные признаки сходимости ряда с положительными членами.

Признаки сравнения рядов с положительными членами.

1-й признак сравнения

Пусть и - ряды с положительными членами, причем а_nдля всех номеров n, начиная с некоторого. Тогда:

1. если ряд 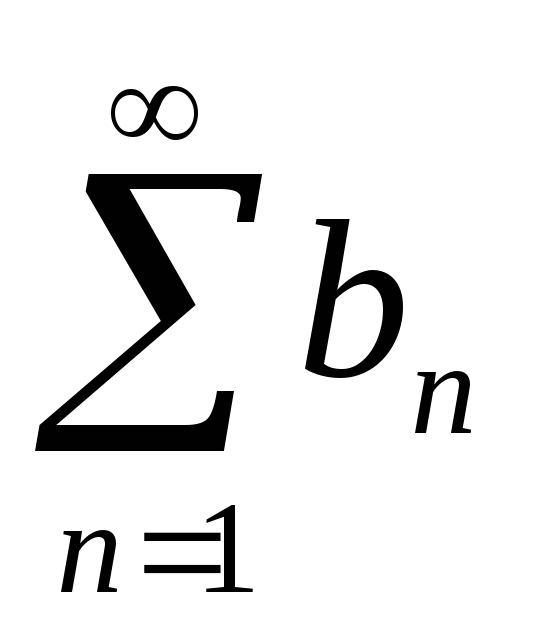сходится, то сходится и ряд

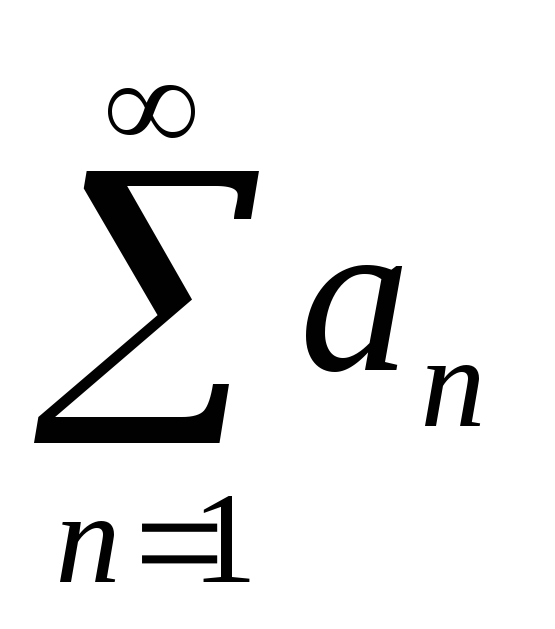
2. если ряд 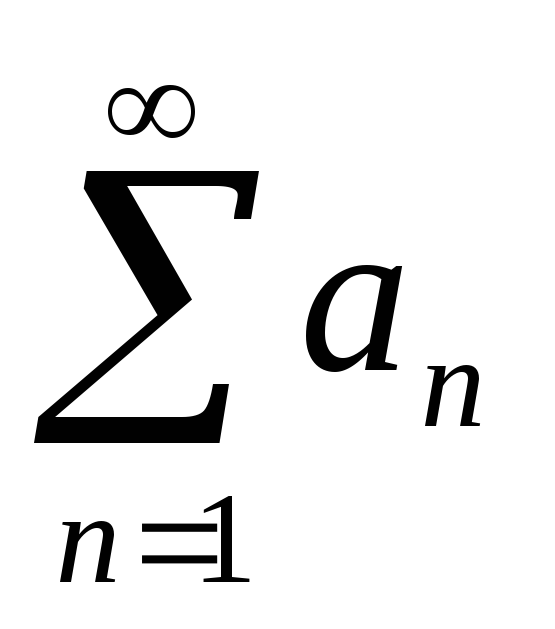расходится, то расходится и ряд

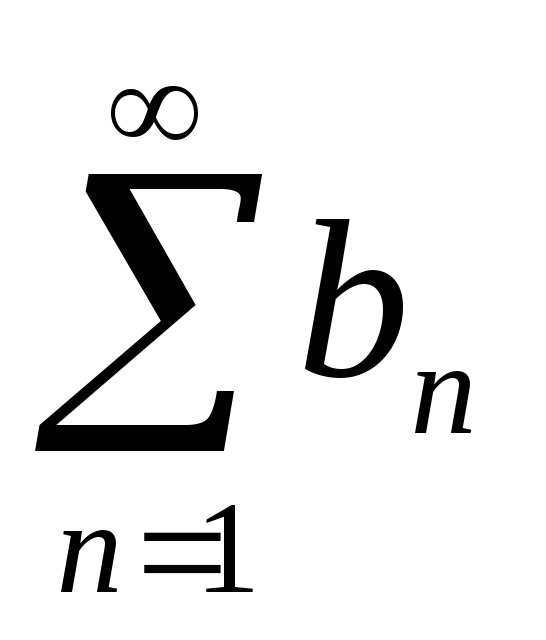
2-й признак сравнения

Пусть и - ряды с положительными членами, причем существует конечный и отличный от нуля предел , тогда ряды и сходятся или расходятся одновременно.

Ряд Дирихле.

Ряд где p>0, называется рядом Дирихле.

Этот ряд сходится при p>1 и расходится при . Частным случаем ряда Дирихле (при р=1) является гармонический ряд .

Задание 3. Исследовать на сходимость по признакам сравнения:

21.	26.
22.	27.
23.	28.
24.	29.
25.	30. .

Признак Даламбера.

Если для ряда с положительными членами

выполняется условие  , то ряд сходится при  и расходится при .

Признак Даламбера не дает ответа, если . В этом случае для исследования ряда применяются другие признаки.

Задание 4. Исследовать на сходимость по признаку Даламбера:

41.	46.
42.	47.
43.	48.
44.	49.
45.	50.

Интегральный признак Коши.

Пусть функция f(x) при x ≥1 удовлетворяет условиям:

1) непрерывна,

2) положительна

3) монотонно убывает.

Тогда числовой ряд , где =f(n), n ≥1 сходится или расходится

одновременно со сходимостью или расходимостью интеграла

Задание 5. Исследовать на сходимость по интегральному признаку Коши:

31. 32. 33. 34. 35.

36. 37. 38. 39. 40.

2. Знакопеременные ряды

2.1 Понятие знакопеременного ряда.

Числовой ряд

называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.

Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки.

,

где для всех (т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно). Например,

;

;

.

Для знакочередующихся рядов имеет место достаточный признак сходимости – признак Лейбница.

2.2 Признак Лейбница. Абсолютная и условная сходимость ряда.

Теорема (Признак Лейбница).

Знакочередующийся ряд сходится, если:

1) последовательность абсолютных величин членов ряда монотонно убывает, т.е. 

;

2) общий член ряда стремится к нулю:.

При этом сумма S ряда удовлетворяет неравенствам

.

Пусть дан знакопеременный ряд , где а_n – произвольные числа (действительные или комплексные). Если ряд , составленный из абсолютных величин его членов, сходится, то данный ряд также сходится.

В этом случае знакопеременный ряд называется абсолютно сходящимся.

если же знакопеременный ряд сходится, а ряд расходится, то данный ряд называется условно сходящимся.

Пример 1.

Исследовать на сходимость ряд

Решение:

1. Исследуем на сходимость ряд из абсолютных величин членов данного ряда:

=.

Сравним этот ряд с рядом . Так как <, то > для всех n.

Ряд расходится, так как расходится ряд (как ряд Дирихле при p=<1). Значит, по 1-му признаку сравнения расходится и ряд .

Итак, исходный ряд не является абсолютно сходящимся.

2. Выясним, сходится ли данный знакочередующийся ряд, применяя признак Лейбница.

А) Проверим, выполняется ли неравенство >для абсолютных величин членов данного ряда:

=>.

Данное неравенство эквивалентно неравенству <, которое верно для любого n=1,2….Значит > для все номеров n=1,2…

Б) Найдем предел общего члена ряда: ==0.

Таким образом, для данного знакочередующегося ряда выполнены оба условия, содержащиеся в признаке Лейбница, откуда следует, что исходный ряд сходится, однако он не является абсолютно сходящимся, поэтому данный ряд сходится условно.

Ответ: ряд сходится условно.

Задание 6. Исследовать на абсолютную и условную сходимость

51.	56.
52.	57.
53.	58.
54.	59.
55.	60. .

3. Функциональные ряды

3.1. Понятие функционального ряда.

Ряд, членами которого являются функции от x, называется функциональным:

.

Придавая  определенное значение, получим числовой ряд

,

который может быть как сходящимся, так и расходящимся.

Если полученный числовой ряд сходится, то точка   называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимости функционального ряда.

Совокупность числовых значений аргумента, при которых функциональный ряд сходится, называется его областью сходимости.

В области сходимости функционального ряда его сумма является некоторой функцией от : .

Определяется она в области сходимости равенством

, где

- частичная сумма ряда.

3.2. Степенные ряды.

Степенным рядом называется ряд вида

Областью сходимости степенного ряда называется множество всех значений , при которых данный ряд сходится.

Числоназывается радиусом сходимости степенного ряда, если при  ряд сходится и притом абсолютно, а при  ряд расходится.

Радиус сходимости  найдем, используя признак Даламбера:

 

,

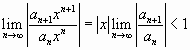
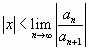т.е. если степенной ряд сходится при любых , удовлетворяющих данному условию и расходится при 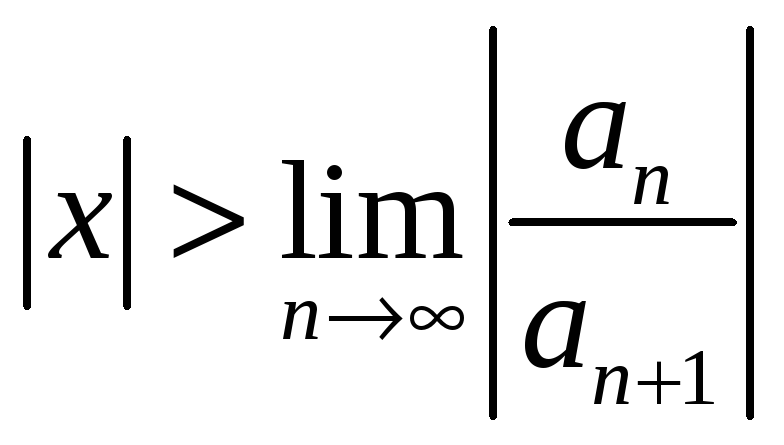.Отсюда следует, что если существует предел

,

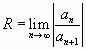
то радиус сходимости рядаравен этому пределу и степенной ряд сходится при , т.е. в промежутке , который называется промежутком (интервалом) сходимости.

Если , то степенной ряд сходится в единственной точке .

На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться.

Сходимость степенного ряда при  и  исследуется с помощью какого-либо из признаков сходимости.

Пример 2. Найти область сходимости ряда

.

Решение. Найдем радиус сходимости ряда:

.

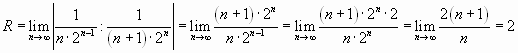Следовательно, ряд сходится при, т.е. при.

Приимеем ряд , который сходится по признаку Лейбница.

Приимеем расходящийся ряд: .

Ответ: областью сходимости исходного ряда является промежуток .

Задание 7. Найти область сходимости степенного ряда.

61.	66.
62.	67.
63.	68.
64.	69.
65.	70.

Ответы:

1) , 2) , 3) ,4) , 5) , 6) , 7) ,8) , 9) , 10) , 11) да, 12) да, 13) да, 14) нет, 15) нет, 16) да, 17) да, 18) нет, 19) нет, 20) да, 21)сх-ся , 22) расх., 23) расх., 24) расх., 25) сх-ся, 26) сх-ся, 27) расх., 28) расх., 29) сх-ся, 30) сх-ся, 31) расх., 32) сх-ся, 33) сх-ся, 34) расх., 35) сх-ся, 36) расх., 37) сх-ся, 38) расх., 39) расх., 40) расх., 41) расх., 42) сх-ся, 43) сх-ся, 44) сх-ся, 45) сх-ся, 46) сх-ся, 47) сх-ся, 48) расх., 49) сх-ся, 50) расх., 51) абс.сх. , 52) усл.сх., 53) усл.сх., 54) усл.сх., 55) абс.сх., 56) абс.сх., 57) абс.сх., 58) абс.сх., 59) усл.сх., 60) усл.сх., 61) (-2;2], 62) , 63) , 64) (-4;4), 65) [-3;1), 66) [-1;5], 67) (-6;2), 68) (-2;1), 69) , 70) (0;4)