Максимальная погрешность

При оценке результатов измерений иногда пользуются понятием максимальнойилипредельной допустимой погрешности, величину которой определяют в доляхилиS. В настоящее время существуют разные критерии установления максимальной погрешности, т.е. границы поля допуска ±, в котором случайные погрешности должны уложиться. Пока общепринятым является определение максимальной погрешности, равной = 3(или 3S). В последнее время на основании информационной теории измерений проф. П.В. Новицкий рекомендует пользоваться величиной = 2.

Доверительные вероятности и интервал

При оценке погрешностей результатов измерения требуется определить точность и надежность полученных результатов для среднего значения и среднего квадратичного отклонения. Пусть означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую чем. Это можно записать в виде

. (14)

Вероятность называетсякоэффициентом надежностиилидоверительнойвероятностью, а интервал значений отдо–доверительным интервалом.

Из выражения (14) следует, что результат измерений не выходит за пределы доверительного интервала с вероятностью, равной , т.е. чем больше доверительный интервал, тем вероятнее, что результаты измерения не выйдут за его пределы и надежность будет выше. Очевидно, что при этом будет больше допустимая погрешность (точность измерения уменьшается). Следовательно, для характеристики величины случайной погрешности необходимо задавать два значения – величину погрешности (доверительный интервал) и величину доверительной вероятности, так как указание только величины погрешности делает задачу неопределенной. Знание доверительной вероятности позволяет оценить степень надежности полученного результата.

На практике степень надежности проводимых измерений зависит от их характера. При большинстве обычных измерений можно ограничиться доверительной вероятностью 0,9 или 0,95, если не требуется более высокая степень надежности. Вероятность определяется законом распределения погрешностей. Для нормального закона распределения значение доверительной вероятности можно определять по (7) или по таблице прил. 3. Так, например, средней квадратичной ошибке соответствует значение доверительной вероятности 0,683; ошибке 2– 0,954; ошибке 3– 0,997.

Ошибки конечного ряда измерений

До настоящего времени искомая величина А определялась большим числом измерений (n 17), и при этом считалось, что она лежит в некотором интервале.При технических измерениях неизвестная величина находится при малом числе измерений(п2), поэтому следует вводить коэффициентt_на количество измерений

или.

Закон изменения коэффициента t_определяется распределением Стьюдента (псевдоним английского статистика Госсета).Распределением Стьюдентапри любомп  2 называется распределение с плотностью вероятностиS(t, п):

,

где п – число измерений;Г– гамма-функция;– нормированное значение случайной величины.

Для любого заданного значения t_доверительную вероятность (надежность) неравенстваопределяют с помощью интеграла:

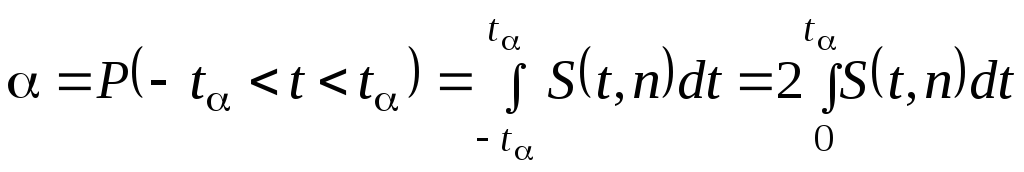
или по таблице прил. 4.

Значения определяются из выражения

.

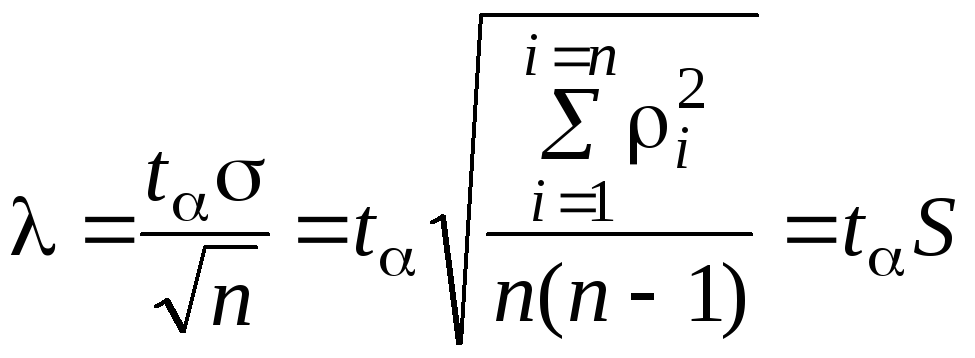Точность, величина надежности и число измерений связаны между собой. Зависимость относительной ошибки от числа измерений при заданной надежности показана в табл. 2.

Таблица 2

Относительная	Число измерений п при величине надежности 
ошибка	0,5	0,7	0,8	0,9	0,95	0,99	0,999
1,0	2	3	4	5	7	11	17
0,5	3	6	9	13	18	31	50
0,3	6	13	20	32	46	78	127
0,2	13	29	43	70	99	171	277
0,1	47	109	166	273	387	668	1089

Как показывают расчеты, при малом числе измерений п и заданной погрешности метод Стьюдента дает меньшую надежность, чем при нормальном законе распределения; при распределение Стьюдента приближается к нормальному.