Оценка погрешностей результатов измерений размеров и параметров деталей при восстановлении автомобилей Средняя арифметическая погрешность

Истинное значение Аизмеряемой величины почти всегда неизвестно, и поэтому определить погрешность каждого отдельного измерения по разности (1) невозможно. Если число измеренийпдостаточно велико, то вместо значенияАберут наиболее достоверное значение – среднее арифметическое:

. (8)

Эта формула математически выражает постулат среднего арифметического: наиболее достоверное значение измеряемой величины, которое можно получить на основании большого ряда измерений, есть среднее арифметическое из полученных значений. Зная его, можно по аналогии с разностью (3) определить разность

, (9)

где _i– отклонение результата измерения от среднего значения.

В отличие от случайной погрешности это отклонение может быть вычислено для каждого измерения. Следует помнить, что сумма отклонений результата измерений от среднего значения равна нулю, а сумма их квадратов – минимальна, т.е. и.

Эти свойства используются при обработке результатов измерений для контроля вычислений.

Сравнивая выражения (9) и (3), видим, что погрешности _iотличаются от случайных погрешностей_iтак, как отличается среднее арифметическое значение ряда измеренийот истинногоА(значения их близки друг другу, но, как правило, не равны). Степень приближения_iк_iбудет тем больше, чем большеп, приможно считать, что_I=_i. Это позволяет все теоретические выводы, относящиеся к случайным погрешностям_i, распространить и на отклонение результата измерений от среднего значения_i. Величину абсолютной ошибки, которая появляется при замене истинного значенияА средним арифметическим значением, можно оценить по их разности

. (10)

Если из уравнения (3) вычесть почленно (9) и учесть (10), то получается, что . Эту погрешность называютслучайной погрешностью результата измерений(среднего арифметического) в отличие от_i, называемойслучайной погрешностью одного измерения. Пользуясь значениемкак конечным результатом ряда измерений, можно допустить погрешность, которая меньше, чем значения_iотдельных измерений из ряда.

Средняя квадратическая погрешность

Величину случайной погрешности чаще оценивают с помощью средней квадратичной погрешности . Определить её по результатам измерений, согласно теории вероятностей, можно по приближенной формуле, вытекающей из (5) и приводимой без доказательства:

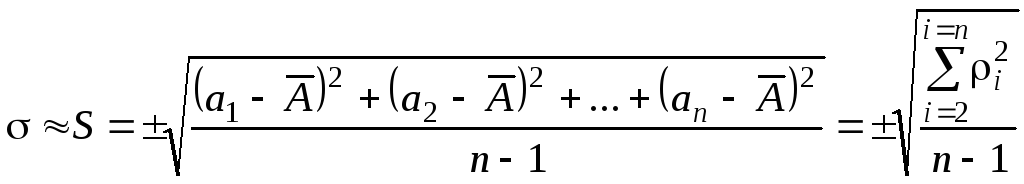, (11)

где _i– отклонение результата измерений от среднего значения;n– число измерений.

Так как среднее арифметическое значение обладает некоторой случайной погрешностью и имеет определенную вероятность в отношении большего или меньшего её значения, теория случайных погрешностей вводит также понятие о среднем квадратичном отклонении среднего арифметического(средняя квадратичная погрешность результата измерений). Возведя в квадрат правую и левую части равенства (10) и проделав дальнейшие преобразования, получим

, (12)

где – приближенное значение квадратичной погрешностиот ряда изп измерений.

Степень приближения кSикопределяется числом измеренийп; в пределе они равны друг другу:и. Из (12) следует, что с увеличением числа измерений точность результатов возрастает, но это происходит медленнее, чем увеличение числа измерений. При обработке результатов измерений иногда определяют среднее относительное квадратичное отклонение

. (13)