
TViMS
.pdfОшибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза. Вероятность ошибки первого рода называют уровнем значимости и обозначают α.
Ошибка второго рода состоит в том, что будет принята неправильная нулевая гипотеза. Вероятность ошибки второго рода обозначают β .
Статистическим критерием (или просто критерием) называют слу-
чайную величину K , которая служит для проверки гипотезы.
Обычно статистические критерии выражаются числами, которые вы-
числяются по вариантам выборки, или находятся теоретически. Значение критерия, найденное на основе выборки наблюдений случайной величины
X , называют выборочным и обозначают Kв . Значение критерия, которое находится по таблице, называется теоретическим и обозначается KТ .
Проверка статистической гипотезы основывается на принципе, в соот-
ветствии с которым маловероятные события считаются невозможными, а
события, имеющие большую вероятность, считаются достоверными.
Критической областью называют совокупность значений критерия,
при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых нулевую гипотезу принимают.
Можно сформулировать следующий основной принцип проверки статисти-
ческих гипотез: если наблюдаемое значение критерия принадлежит крити-
ческой области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.
Критическими точками (границами) kкр называют точки, отделяющие критическую область от области принятия гипотезы.
113

Правосторонней называют критическую область, определяемую нера-
венством K kкр , где kкр – положительное число.
Левосторонней называют критическую область, определяемую нера-
венством K kкр , где kкр – отрицательное число.
Двусторонней называют критическую область, определяемую неравен-
ством K k1 K k2 , где k2 k1 .
В частности, если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется неравенствами (в предположении, что kкр 0 ) K  kкр , K kкр или K kкр .
kкр , K kкр или K kкр .
Для отыскания критической области задаются уровнем значимости и
ищут критические точки, исходя из следующих соотношений:
для правосторонней критической области P K |
kкр |
α |
kкр |
0 ; |
||||||||||
для левосторонней критической области P K |
kкр |
α |
kкр |
0 ; |
||||||||||
для двусторонней симметричной критической области |
|
|||||||||||||
P K k |
|
α |
k |
|
0 , P K |
k |
|
|
α |
. |
|
|
|
|
кр |
2 |
кр |
кр |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проверка значимости статистической гипотезы при помощи критерия |
||||||||||||||
значимости может быть разбита на следующие этапы: |
|
|
||||||||||||
сформулировать проверяемую |
H0 и альтернативную H1 гипотезы; |
|||||||||||||
назначить уровень значимости |
; |
|
|
|
|
|
|
|
|
|||||
выбрать статистический критерий; |
|
|
|
|
|
|
|
|
||||||
определить теоретическое KT |
и выборочное |
Kв |
значения критерия; |
|||||||||||
определить критическую область Vk ; |
|
|
|
|
|
|
|
|||||||
принять статистическое решение: если Kв |
Vk , то гипотезу |
H0 |
принять, т. е. счи- |
|||||||||||
тать, что гипотеза H 0 не противоречит результатам наблюдений; если Kв Vk , то отклонить гипотезу H 0 как не согласующуюся с результатами наблюдений.
114

2.6. Критерий Пирсона 2 (хи-квадрат)
Этот критерий был введен английским математиком К. Пирсоном (1857
– 1936 г.). Критерий служит для проверки гипотезы о виде распределения
случайной величины X .
Итак, пусть имеется сгруппированный статистический ряд, разбитый
на k интервалов, где k заранее выбранное число, mi |
число вариант, |
|
попадающих в i интервал, n объем выборки, |
pi P xi 1 |
X xi веро- |
ятность попадания случайной величины X в i |
тый интервал при выбран- |
|
ном законе распределения случайной величины. При этих условиях Пир-
сон предложил в качестве критерия K рассмотреть случайную величину
2 |
|
mi |
2 |
|
|
|
|
|
|
|
|
|||
k |
npi |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, ( mi |
случайные величины). |
||||||
|
i 1 |
|
|
npi |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Он доказал, что |
2 при больших k практически не зависит от гипотети- |
|||||||||||||
ческого распределения и определяется функцией плотности |
||||||||||||||
|
|
|
|
1 |
|
|
|
|
r |
1 |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r |
u |
|
|
|
|
|
|
u 2 |
e 2 , u |
0, |
||||
|
|
|
r |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2r / 2 Г |
|
u |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
где r |
число степеней свободы, определяемое по формуле r k m 1, |
|||||||||||||
здесь m |
число параметров гипотетического закона распределения, под- |
|||||||||||||
лежащих определению по опытным данным. |
||||||||||||||
|
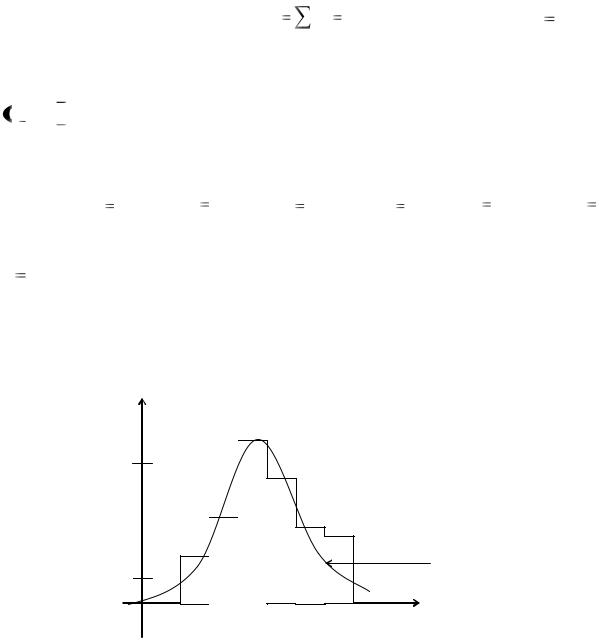
График функции плотности |
r u имеет вид (рис. 3): |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r u |
|
||
u
115

Рис. 3
Критерий 2 заключается в следующем. По опытным данным считают выборочное значение критерия Пирсона
|
k |
mi |
npi |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
, |
|
|
|
|||
в |
|
|
npi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
i 1 |
|
|
|
|
|
|
|
|
( mi |
– выборочные частоты). |
|
|
|
|||||
По таблице критических точек распределения 2 |
(см. приложения) по за- |
||||||||
данному уровню значимости |
и числу степеней свободы r находят тео- |
||||||||
ретическое значение критерия Пирсона T2 . |
|
||||||||
|
Если значение |
2 |
|
|
2 |
||||
|
в окажется больше или равно |
T , то гипотезу отвер- |
|||||||
гают. Если же |
2 |
меньше |
2 |
, то гипотезу считают не противоречащей |
|||||
в |
T |
||||||||
опытным данным.
При использовании критерия хи-квадрат рекомендуем промежуточные ре-
|
|
|
|
mi |
npi |
|
|
2 |
|
m |
np |
2 |
|
|
|
xi 1, xi |
mi |
pi |
npi |
mi |
npi |
|
i |
|
i |
|
|
||||
|
|
|
npi |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x0 , x1 |
m1 |
p1 |
np1 |
m1 |
np1 |
m np 2 |
|
m1 |
np1 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
1 |
|
|
np1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
mk |
|
2 |
|
||
xk 1 , xk |
mk |
pk |
npk |
mk |
npk |
mk |
npk |
2 |
|
npk |
|
||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
npk |
|
|
|
|
зультаты заносить в таблицу:
Замечание. Разбивку на интервалы надо производить так, чтобы в каждом из них было 5 – 10 наблюдений. Интервалы, содержащие мало наблюде-
ний, рекомендуется объединять с соседними.
116
Пример 1. Даны результаты наблюдений некоторой случайной величины X . Проверить гипотезу о ее нормальном распределении.
интервалы |
3,5-4,5 |
4,5-5,5 |
5,5-6,5 |
6,5-7,5 |
7,5-8,5 |
8,5-9,5 |
|
|
|
|
|
|
|
|
|
число |
6 |
13 |
25 |
16 |
11 |
9 |
|
вариант |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Решение
1. Построим гистограмму относительных частот (рис. 4), данные для ее
построения занесем в таблицу ( n |
mi 80 , длина интервалов l 1). |
|
xi 1, xi |
|
(4) |
|
|
(5) |
|
(6) |
|
(7) |
|
(8) |
|
(9) |
|
||||||||
|
|
3,5-4,5 |
4,5-5,5 |
5,5-6,5 |
6,5-7,5 |
7,5-8,5 |
8,5-9,5 |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mi |
|
|
6 |
|
|
13 |
|
25 |
|
16 |
|
11 |
|
9 |
|
|||||||
|
ni |
|
|
|
6 |
|
0,075 |
13 |
0,1625 |
25 |
0,3125 |
16 |
0,2 |
11 |
0,1375 |
9 |
0,11125 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
80 |
|
80 |
80 |
80 |
80 |
80 |
||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
h |
mi |
|
0,075 |
|
0,1625 |
0,3125 |
0,2 |
|
0,1375 |
0,1125 |
||||||||||||
|
nl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
График функции плотности
x
117

Рис. 4
2. По виду гистограммы можно предположить, что наблюдаемая случайная величина имеет нормальное распределение – N a, 2 .
Функция плотности вероятности нормального распределения имеет вид
|
1 |
|
|
x |
a 2 |
|
f x |
|
e |
2 |
2 |
||
|
|
|
|
|
||
2 |
|
|
||||
|
|
|
|
|
||
, где параметры a и неизвестны.
В качестве значений параметров распределения возьмем их оценки, полученные на основе опытных данных. Оценкой параметра a является величина
__ |
1 |
|
k |
|
|
|
|
x m |
|
x |
m |
|
|
... |
x |
m |
|
|
|
|
|
|
|
||||||||||
|
x |
|
|
|
x |
m |
|
|
1 1 |
|
2 |
|
|
|
2 |
|
|
k |
|
k |
, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n i |
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
оценкой параметра |
2 |
|
является величина |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
__ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x |
|
|
|
x |
m . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
n |
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В этих формулах xi |
– середина i –того интервала. |
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
|
6 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6,5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
x m |
|
|
|
|
|
4 6 |
|
5 13 |
6 25 |
|
7 16 |
8 11 |
9 9 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
n i |
|
i |
i |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
s2 |
|
|
|
1 |
|
|
6 |
|
|
|
|
|
|
2 |
|
|
|
|
|
6,5 2 |
|
|
6,5 2 |
|
6 6,5 2 25 |
||||||||
|
|
|
|
|
|
x |
|
|
x |
|
m |
|
|
|
|
|
|
4 |
6 5 |
13 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
n |
|
|
|
i |
|
|
|
|
|
|
i |
|
|
79 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7 |
6,5 2 |
|
11 |
|
|
8 |
|
|
|
6,5 2 |
9 1,97 |
|
s |
1,97 1,4. |
|
||||||||||||||||||
Итак, выдвигаем гипотезу о том, что изучаемая случайная величина имеет функцию плотности вероятности
|
|
1 |
|
|
|
( x 6,5)2 |
|
f (x) |
|
|
|
e |
2 1,97 . |
||
|
|
|
|
||||
|
|
|
|
||||
|
|
||||||
1,4 |
|
2 |
|
|
|
|
|
118
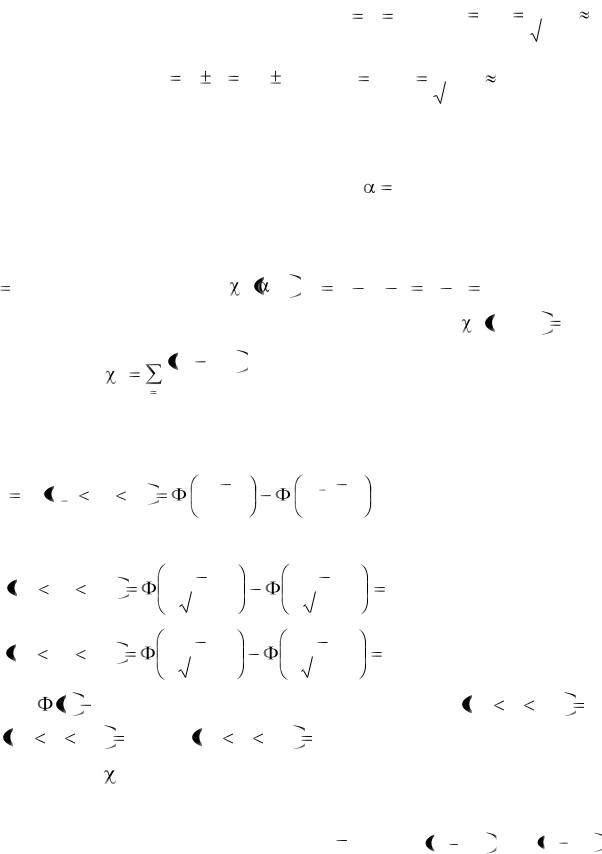
Ее график построим на том же чертеже, что и гистограмму (рис. 4). Для построе-
|
|
|
|
|
|
ymax |
0,4 |
|
|
0,4 |
|
0,28 |
|||||
ния достаточно найти точки максимума |
xmax x 6,5, |
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||
s |
|
|
|
||||||||||||||
1,97 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и точки перегиба xпер x s 6,5 1,4 , |
yпер |
0,24 |
0,24 |
|
|
0,17 |
. Затем эти |
||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
s |
|
|
|
|
|||||||||||
|
|
1,97 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
точки следует соединить плавной линией, учитывая форму кривой нормаль-
ного распределения (рис. 4). |
|
3. Зададимся уровнем значимости, например, |
0,05 . Для получения надеж- |
ных выводов на основе критерия хи-квадрат нужно объединить первый интервал, содержащий мало наблюдений, со вторым интервалом. Тогда имеем всего
k |
5 интервалов. Определим |
2 |
, r |
, r k m 1 5 3 |
|
2 (r – число сте- |
|||
T |
|
||||||||
|
|
|
|
|
|
|
|
|
|
пеней свободы, m – число неизвестных параметров). Итак, |
2 |
0,05; 2 5,99 . |
|||||||
|
|
|
|
|
|
|
|
T |
|
|
|
2 |
k |
mi npi |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
4. |
Вычислим |
в |
|
|
|
Для этого сначала вычислим вероятности, |
|||
|
npi |
|
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
i 1 |
|
|
|
|
|
|
попадания исследуемой случайной величины в каждый интервал, согласно гипотезе. В случае нормального распределения они вычисляются по формуле:
pi P xi 1 |
|
X |
xi |
xi |
x |
|
|
|
xi 1 |
x |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
s |
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P 3,5 |
X |
5,5 |
5,5 |
|
6,5 |
|
|
3,5 |
6,5 |
|
|
0,22 , |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1,97 |
|
|
|
|
1,97 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
P 5,5 |
X |
6,5 |
6,5 |
|
6,5 |
|
|
|
5,5 |
6,5 |
|
|
|
0,26 |
, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1,97 |
|
|
|
|
|
1,97 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где |
x |
|
|
функция |
Лапласа. |
Аналогично |
|
|
P 6,5 x |
7,5 |
0,16, |
||||||||||||||||||||||||
P 7,5 |
x |
8,5 |
0,16, P 8,5 |
x |
9,5 |
|
|
0,06. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Вычисления |
2 удобно вести, |
фиксируя промежуточные результаты в |
|||||||||||||||||||||||||||||||||
таблице. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
mi |
|
|
pi |
|
|
|
|
npi |
|
|
|
|
|
|
|
mi |
npi |
|
|
m |
|
np |
2 |
|
mi |
npi |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
119
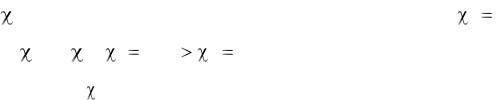
19 |
0,22 |
17,6 |
1,4 |
1,96 |
0,11 |
|
|
|
|
|
|
25 |
0,26 |
20,8 |
4,2 |
17,64 |
0,85 |
|
|
|
|
|
|
16 |
0,26 |
20,8 |
4,8 |
23,06 |
1,11 |
|
|
|
|
|
|
11 |
0,16 |
12,8 |
1,8 |
3,24 |
0,25 |
|
|
|
|
|
|
9 |
0,08 |
4,8 |
4,2 |
17,64 |
3,89 |
|
|
|
|
|
|
Величина |
2 |
|
|
|
|
|
|
2 |
6,21. |
в |
равна сумме значений в последнем столбце таблицы в |
||||||||
5. Сравним |
|
2 |
2 |
: |
2 |
6,21 |
2 |
5,99. Таким образом, при выбранном |
|
|
в и |
T |
в |
T |
|||||
уровне значимости |
|
2 |
принадлежит критической области Vk , а значит ги- |
||||||
|
в |
||||||||
потезу о нормальном распределении следует отвергнуть. Следует отм е- тить, что вероятность того, что мы ошибаемся, меньше 0,05.
3. Линейная корреляция
Две случайные величины X и Y могут быть функционально зависимы,
статистически зависимы или независимы. Наиболее простой формой зависи-
мости между величинами является функциональная зависимость, при которой каждому значению одной величины соответствует определенное значение дру-
гой. Однако на практике связь между величинами носит случайный характер.
Статистической называется зависимость, при которой изменение одной из случайных величин ведет к изменению закона распределения другой величины. В частности, если при изменении одной из величин изменяется среднее значение другой, то статистическая зависимость называется кор-
реляционной. Статистическая зависимость более сложна, чем функцио-
нальная. Она возникает, если одна величина зависит не только от другой,
но и от ряда прочих случайных факторов. Примерами статистической за-
висимости являются связи между ростом ребенка и его возрастом, между урожайностью ягодных культур и их рыночными ценами, между темпера-
турой закалки и твердостью стали и т. д.
120

Пусть произведено n независимых опытов, в которых наблюдались случайные величины X и Y . В результате опытов получены пары чисел
____ |
____ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
xi , y j (i 1, l ; j |
1, k) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Данные сводят в корреляционную таблицу: |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
X /Y |
|
y1 |
y2 |
|
… |
yk |
|
nx |
|
|
|
|
|
|
|||||
|
|
|
|
|
yx |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
n |
n |
|
|
n |
|
nx |
|
|
|
|
|
|
||||
|
|
|
|
… |
|
|
|
y |
x |
|||||||||||
|
|
1 |
|
11 |
12 |
|
|
1k |
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
n |
|
n |
|
|
|
|
|
|
nx |
|
|
|
|
|
|
|
2 |
|
21 |
22 |
… |
|
|
|
2 |
|
y |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
|
|
n p |
np |
|
|
n |
|
|
nx |
|
|
|
|
|
|
|||
|
l |
|
2 |
|
lk |
|
l |
|
y |
xl |
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
ny |
|
ny |
ny |
2 |
|
ny |
k |
n |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В первой строке таблицы указаны наблюденные значения случайной величины Y : y1 , y2 ,..., yk ; в первом столбце – величины X : x1, x2 ,..., xl . На
пересечении строк и столбцов вписаны частоты ni j наблюдаемых пар значений случайных величин. Пустая клетка означает, что соответствую-
щая пара чисел в результате опытов не наблюдалась. В столбце nx записа-
ны суммы частот строк, в строке ny – суммы частот столбцов, причем
nx |
ny |
n – объем выборки. |
i |
|
j |
__
Назовем условным средним y x среднее арифметическое значений случай-
ной величины Y , соответствующих значению X x .
__
Уравнение yx f (x) называют уравнением регрессии Y на X ; функ-
цию f (x) называют регрессией Y на X , а ее график – линией регрессии.
Если функция регрессии f (x) известна, то можно по значению одной слу-
121
чайной величины прогнозировать значение другой случайной величины. Корреляция называется линейной, если линия регрессии является прямой,
__ |
|
|
|
|
|
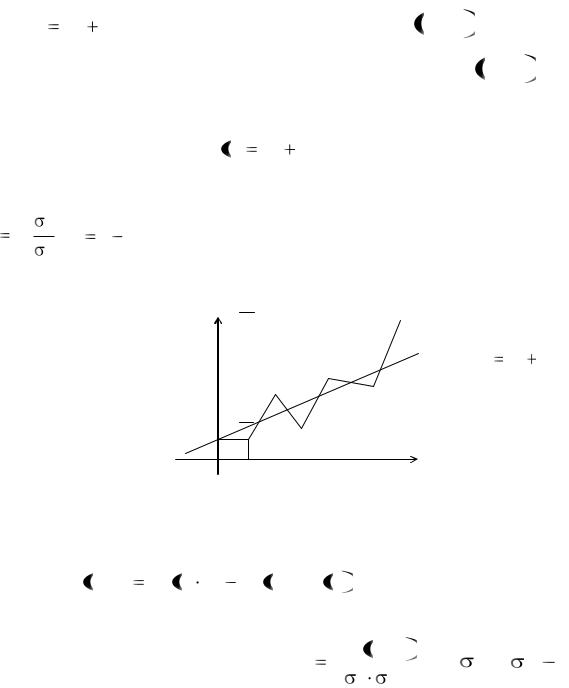
т. е. yx ax b. Ломаная, соединяющая точки Mi xi , yxi |
, называется эм- |
||||
|
|
|
|
||
пирической (опытной) линией регрессии. Если точки Mi |
xi , yxi распола- |
||||
гаются около некоторой прямой, то в качестве уравнения теоретической линии регрессии берется f x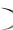 ax b , где коэффициенты находятся по формулам:
ax b , где коэффициенты находятся по формулам:
a rxy y x
__ |
__ |
; b y |
a x , (rx y определен ниже). |
yx
yx ax b
y1
x1
Рис.5
Ковариацией двух случайных величин X и Y называется числовая характе-
ристика cov X ,Y  M X Y
M X Y 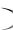 M X
M X  M Y .
M Y .
Коэффициентом корреляции между случайными величинами |
X и Y |
|||||
называется безразмерная величина r |
cov X ,Y |
; где |
|
и |
|
средние |
|
x |
y |
||||
xy |
|
|
|
|
||
x y
квадратические отклонения величин X и Y .
Коэффициент корреляции rx y характеризует степень тесноты линейной зависимости между случайными величинами X и Y , при этом связь тем
122
