2. Расчет линейных электрических цепей переменного тока
К
зажимам электрической цепи, схема
замещения которой приведена на рисунке
2.1, подключен источник синусоидального
напряжения
В,
Град,
Гц. С включёнными в схему элементами:
Ом,
Ом,
мГн,
мГн,
мкФ,
мкФ
Выполнить следующее:
-определить реактивные сопротивления элементов цепи;
определить действующие значения токов во всех ветвях цепи;
записать уравнение мгновенного значения тока источника;
составить баланс активных и реактивных мощностей;
построить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений.
Рисунок 2.1 - Электрическая схема для определения эквивалентного сопротивления
Определяем реактивные сопротивления элементов цепи:
(Ом)
(Ом)
(Ом)
(Ом)
Расчет токов в ветвях цепи выполняем методом эквивалентных преобразований.
Представим схему, приведенную на рисунке 2.2, в следующем виде:
Рисунок 2.2 - Преобразованная однофазная электрическая цепь переменного тока
Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:
(Ом)
(Ом)
(Ом)
(Ом)
(Ом)
(Ом)
(Ом)
Выразим действующее значение напряжений в комплексной форме
(В)
Вычисляем токи ветвей и общий ток цепи:
(А)
(А)
(А)
(А)
(А)
Записываем уравнение мгновенного значения тока источника:
(А)
(А)
Комплексная мощность цепи:
Где:
(Вт)
(
)
(вар)
Активная
и реактивная
мощность приёмников
(Вт)
(вар)
Баланс мощностей выполняется:
;
Рассчитываем напряжения на элементах схемы замещения цепи:
(В)
(В)
(В)
(В)
(В)
(В)
Строим
топографическую векторную диаграмму
на комплексной плоскости. Выбираем
масштаб:
(А/см),
(В/см).
Определяем длины векторов токов и напряжений:
(см)
(см)
(см)
(см)
(см)
(см)
(см)
(см)
(см)
(см)
(см)
(см)
Рисунок 2.3 - Топографическая диаграмм
3. Расчет трехфазных линейных электрических цепей переменного тока
линейный электрический цепь сопротивление
В цепи, изображенной на схеме (рисунке 3.1), потребители трехфазного тока соединены звездой.
Известно линейное напряжение Uл = 220 В и сопротивления фаз: RB=12 Ом, RC=8 Ом, XLB=16 Ом, XCA=25 Ом, XCC=6 Ом.
Определить полные сопротивления фаз, фазные токи и ток в нейтральном проводе, активную, реактивную и полную мощности каждой фазы и всей цепи.
Рисунок
3.1 - Схема для расчёта потребителей
трехфазного тока
Строгий аналитический расчет трехфазных цепей производится символическим методом, т. е. в комплексной форме.
Выразим в комплексной форме фазные напряжения:
(В)
(В)
(В)
(В)
Выразим сопротивления фаз в комплексной форме:
(Ом)
(Ом)
(Ом)
Находим комплексы фазных токов:
(А)
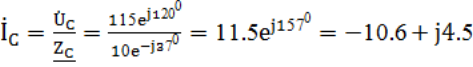(А)
(А)
Вычисляем ток в нейтральном проводе:
(А)
Модуль
,
аргумент
.
Вычисляем мощности фаз и всей цепи
(
)
где:
(
);
=0
(Вт);
(вар);
(
)
где:
(
);
(Вт);
(вар);
(
)
где:
(
);
(вар);
Тогда:
(
)
где
(
);
(Вт);
(вар);
Строим векторную диаграмму цепи.
На векторной диаграмме под углом 120° друг относительно друга строятся векторы фазных напряжений одинаковой длины.
Векторы фазных токов строятся в масштабе под вычисленными углами φ по отношению к фазным напряжениям. Ток в нейтральном проводе равен геометрической (векторной) сумме фазных токов:
Рисунок 3.2 - Векторная диаграмма токов и напряжений при соединении "звездой"
ЗАКЛЮЧЕНИЕ
В курсовой работе состояла из трех частей. Задание первой части составлено по темам: "Методы расчета линейных электрических цепей постоянного тока". Задание второй части составлено по теме: "Расчет однофазных линейных электрических цепей переменного тока". Задание третьей части составлено по теме "Трехфазные электрические цепи".
В курсовой работе выполнено:
составлена на основании закона Кирхгофа система уравнения для определения токов во всех ветвях схемы;
определены токи во всех схемах используя метод контурных токов;
определены токи во всех ветвях схемы на основании метода наложения;
составлен баланс мощностей для заданной схемы;
представлены в виде таблиц и сравнены результаты расчетов токов по пунктам 2и 3;
определен ток во второй ветви методом эквивалентного генератора;
построена потенциальная диаграмма для любого замкнутого контура, включающего обе ЭДС;
определены реактивные сопротивления элементов цепи;
определены действующие значения токов во всех ветвях цепи;
записано уравнение мгновенного значения тока источника;
составлен баланс активных и реактивный мощностей;
построена векторная диаграмма токов, совмещенная с топографической векторной диаграммой напряжения;
произведен расчет трехфазных линейных цепей переменного тока.