Лекция 6

Лекция 6

Дифференцирование обобщённой функции

В отличие от обычных функций, которые не всегда имеют производные (в обычном смысле), обобщённые функции имеют производные всех порядков, которые являются также обобщенными функциями. Если функция непрерывна и обладает непрерывной производной, то можно построить функционал

(26)

Интегрируя по частям и учитывая, что функция обращается в нуль вне некоторого интервала [a, b], получим

(27)

Это равенство и кладётся в основу общего определения производной обобщённой функции.

Пусть f – произвольный линейный непрерывный функционал на основном пространстве K. Тогда, функционал g, заданный формулой

(28)

называется производной от функционала f и обозначается

или (29)

Учитывая (26) и (27) имеем

(30)

Легко убедится, что функционал g также является линейным, непрерывным функционалом на пространстве K.

Легко проверить, что выполняются обычные правила дифференцирования, а именно:

- Производная суммы равна сумме производных

( f₁ + f₂ ) ^/ = f₁^/ + f₂^/ (31)

- Постоянный множитель выносится за знак производной

( a f₁) ^/ = a f ^/, a – const (32)

- Произведение бесконечно дифференцируемой функции a(x) на обобщённую функцию f :

(a(x) f ) ^/= a ^/(x) f + a f ^/ (33)

Действительно, мы имеем:

Для нескольких независимых переменных:

Определим для каждой обобщённой функции f её частные производные по каждому из независимых переменных

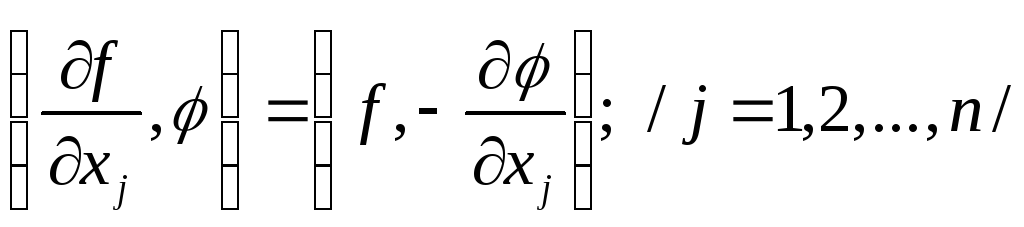(34)

Поскольку, результат дифференцирования обобщённой функции есть снова обобщённая функция, можно определить производную любого порядка

и т.д.

Т.о. все обобщённые функции бесконечно дифференцируемы.

Рассмотрим примеры для случая функции одной независимой переменной.

Пример 1. Рассмотрим функцию Хевисайда

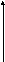
Отвечающий ей функционал обозначим также . Согласно формуле (28) функционал действует на основную функцию так:

(35)

/ по определению “хорошей” или “основной” функции /

Таким образом, в силу определения дельта функции (5)

(36)

Следующая производная

и т.д.

Для смещённой дельта функции из (36) получим

(37)

П ример 2 Пусть f (x) – кусочно-непрерывная функция с кусочно-непрерывной производной f ^/(x), в точках разрывы I рода со «скачками» h₁, h₂, … ,

Производная f ^/(x) определена всюду кроме конечного числа точек. Найдём производную от функционала f , соответствующего функции f(x).

Введём функцию:

(38)

Очевидно, что она всюду непрерывна и имеет производную f ^/(x) всюду, кроме конечного числа точек. Как показано ранее (см.(28)), функционал f ^/ соответствует функции f ^/(x), если функции f(x) и f ^/(x) непрерывны. Тогда, из равенства (38), дифференцируя его, получим

Откуда

(39)

Т.е. если f(x) кусочно-непрерывная функция с кусочно-непрерывной производной, то при дифференцировании, каждая точка разрыва I рода функции f(x) со «скачком» h_k добавляет в выражение производной слагаемое .

Разрывы обобщённых функций ведут к дельта функциям в производных.

Пример 3 Найти производную обобщённой функции .

Здесь мы и встречаемся с необходимостью регуляризации расходящегося интеграла.

Вставка: Регуляризация расходящегося интеграла.

Пусть f(x) – функция, локально интегрируемая всюду, кроме т. x₀, в которой имеется неинтегрируемая особенность (например, на оси). Тогда, интеграл

(40),

где - основная функция, вообще говоря, расходится. Но он сходится, если равна нулю в окрестности т. x₀. Если можно доопределить, возникающий при этом функционал, который на основные функции действует по формуле (40), то такой функционал f называется регуляризацией расходящегося интеграла (40) (или регуляризацией функции f(x)).

Так, для , можно положить:

с любыми a > 0 и b > 0.

Продолжение Примера 3

Запишем

Как известно, полученный предел называется главным значением по Коши оси . Мы его будем обозначать . Соответствующую обобщённую функцию мы будем обозначать 1/x, тогда . Функционал 1/x не регулярный, но совпадает с функцией 1/x всюду, кроме x = 0.

Пример 4. Найдём производную от логарифма комплексной функции (это также обобщённая функция): ; определяемой равенством

если , где , а , то

Тогда

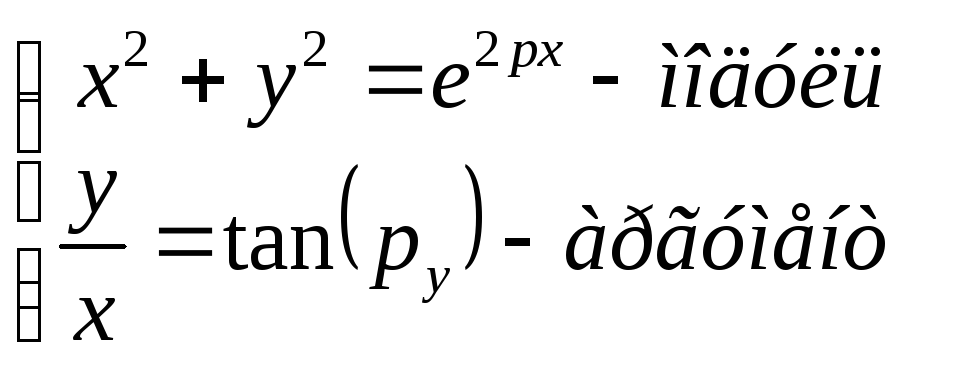
Пояснение1:

Можно записать

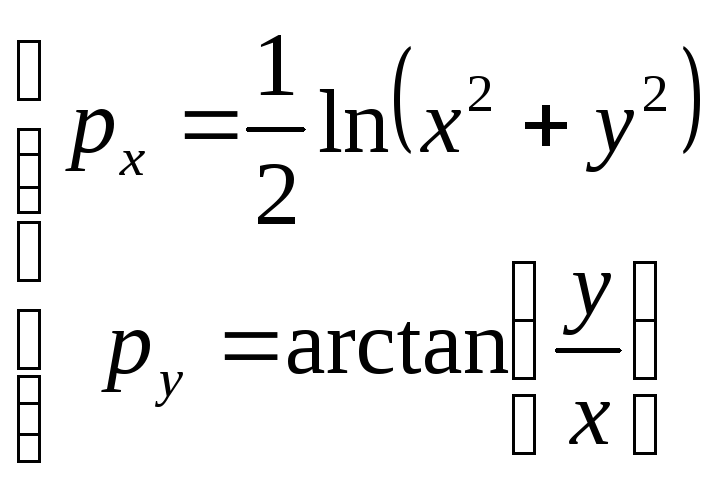
Модуль комплексного числа

Переходим к пределу, при

п ричём ;

- по модулю всегда ограничено и стремится к пределу при Т.е. имеет скачок величиной .

Перепишем:

при переходя к пределу, видим, что

.

Т.к. и учитывая, что , получим . Тогда ,

поэтому

Т.е. ещё раз заметим, что надо внимательно следить за разрывами. Они ведут к дельта функциям.

Пояснение 2:

Исходя из:

и при

Значит:

или

Пояснение 3.

укручается и становится ступенькой. В пределе – это функция Хевисайда, только перевёрнутая. При x замена на (-x) мы получим Хевисайд:

.

Пример 5. Для случая нескольких независимых переменных.

Для непрерывных функций f(x) с кусочно-непрерывными частными производными, дифференцирование соответствующих регулярных функционалов, приводит снова к регулярным функционалам.

Найдем в трехмерном пространстве результат применения оператора Лапласа к регулярному функционалу, определенному функцией , где

Функция гармоническая в любой области, не содержащей начала координат, так, что выражение , при , обращается в нуль (в обычном смысле).

Покажем это. Запишем оператор Лапласа

тогда

;

проделав аналогично для других переменных, имеем

Итак, во всех точках, кроме . В окрестности этой точки надо действовать аккуратно с помощью функционала. Рассматривая оператор Лапласа в пространстве обобщенных функций, находим

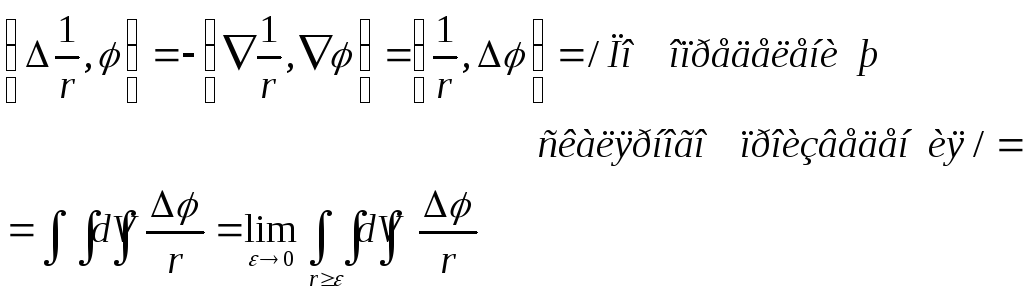
Теперь, по формуле Грина для шарового слоя (

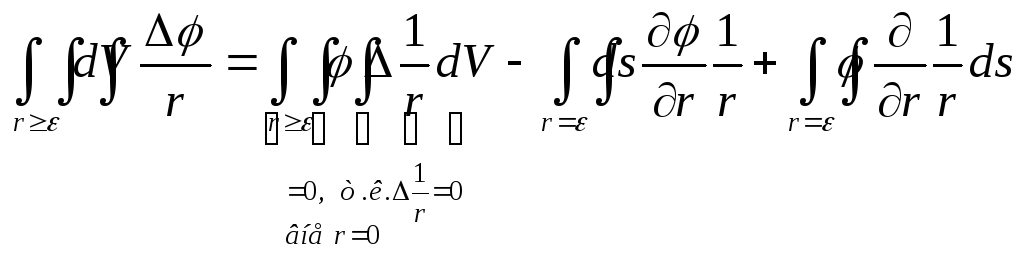
dS – есть элемент сферы

Пояснение: формула Грина в общем случае

Теперь простые оценки

/

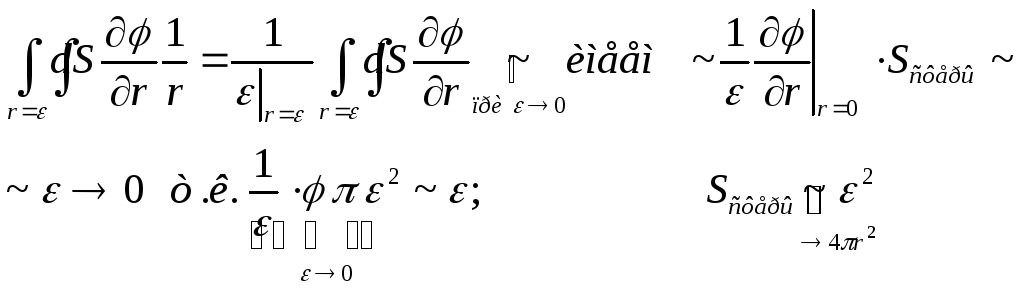
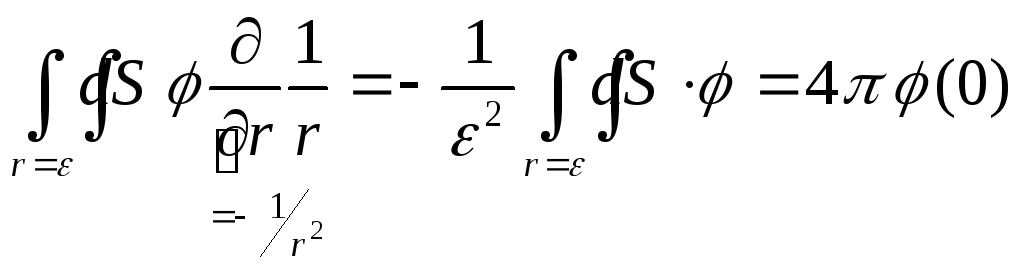
И тогда

т.е. через функционалы

Но отсюда вытекает, что

т.е. вторая производная в трехмерном пространстве равна дельта-функии.

Аналогично, в двумерном пространстве

Пояснение :

где a настолько велико, что вне шара функция тождественно равна нулю.