РАЗНОЕ3 / физика / Новая папка / Лабораторные работы / лаба 2

РХТУ им. Д.И. Менделеева

Кафедра Электротехники и Электроники

Лабораторная работа № 2

Разветвленная электрическая цепь синусоидального тока

с активно - реактивным сопротивлениями.

Резонанс токов.

Выполнили студенты ИХТ факультета

группы И-24

Михеева Е.В.

Антипова Ф.В.

Фокина В.И.

Проверил ведущий преподаватель: 5TEEN-jeep

HomeСтудия

Москва

2004

Цель работы: Исследование режимов работы электрической цепи при параллельном соединении потребителей электроэнергии с активно – реактивными сопротивлениями, определение параметров цепи, установление условий возникновения резонанса токов.

Принципиальная схема:

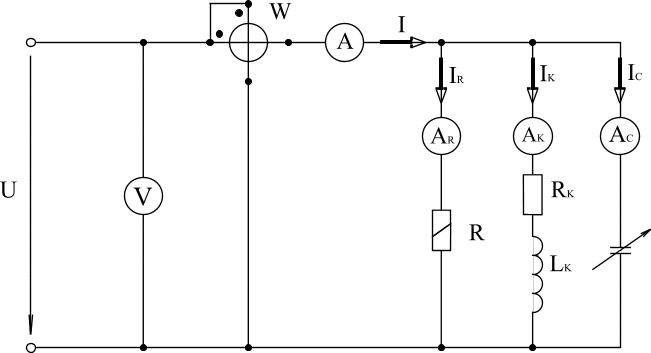
1.R – цепь.

№	Установить		Измерить			Вычислить
	f,Гц	U, В	I, A	P, Bm	IR, A	YR, Cм	S, BA	cosφ
1	50	127	1.389	176.5	1.389	0,011	176,403	1
2	50	220	2.407	529.5	2.407	0,011	529,54	1
3	100	220	2.407	529.5	2.407	0,011	529,54	1

Y_R = I_R/U; S = U∙I; cosφ = P/S.

2.C – цепь.

№	Установить		Измерить			Вычислить
	f,Гц	U, В	I, A	P, Bm	IС, A	Yc, Cм	S, BA	cosφ
1	50	127	0.838	0	0.838	0,007	106,426	0
2	50	220	1.451	0	1.451	0,007	319,22	0
3	100	220	2.903	0	2.903	0,013	638,66	0

Y_C = I_C/U; S = U∙I; cosφ = P/S.

3.R – C – цепь.

№	Установить		Измерить				Вычислить
	f,Гц	U, В	I, A	P, Bm	IR, A	IС, A	YR, Cм	Yc, Cм	Y, Cм	S, BA	cosφ
1	50	127	1,623	176,5	1,389	0,838	0,011	0,007	0,013	206,121	0,856
2	50	220	2,811	529,5	2,407	1,451	0,011	0,007	0,013	618,42	0,856
3	100	220	3,771	529,5	2,407	2,903	0,011	0,013	0,017	829,62	0,313

Y_R = I_R/U; Y_C = I_C/U; Y = I/U; S = U∙I; cosφ = P/S.

4.R – L – цепь.

№	Установить		Измерить			Вычислить
	f,Гц	U, В	I, A	P, Bm	IК, A	YK, Cм	GK, Cм	BK, Cм	S, BA	cosφ
1	50	127	0,952	9,1	0,952	0,008	0,008	0	120,904	0,075
2	50	220	1,649	27,2	1,649	0,008	0,008	0	362,78	0,075
3	100	220	0,826	6,8	0,826	0,004	0,004	0	181,72	0,037

Y_K = I_K/U; G_K = I/U; B_K = (Y_K² - G_K²)^0.5; S = U∙I; cosφ = P/S.

5.R – L – C – цепь.

№	Установить		Измерить					Вычислить
	f,Гц	U, В	I, A	P, Bm	IR, A	IL, A	IC, A	Y, Cм	YR, Cм	YL, Cм	Yc, Cм	S, BA	cosφ
1	50	127	1.394	176.5	1.389	0.955	0.838	0,011	0,011	0,008	0,007	177,038	1
2	50	220	2.416	529.5	2.407	1.654	1.451	0,001	0,011	0,008	0,007	539,2	0,982
3	100	220	3.178	529.5	2.407	0.827	2.903	0,014	0,011	0,004	0,013	699,16	0,8

Y = I/U; Y_R = I_R/U; Y_L = I_L/U; Y_C = I_C/U; S = U∙I; cosφ = P/S.

6.Резонанс.

№	Установить		Измерить					Вычислить
	C, мкФ	U, B	I, A	P, Bm	IR, A	IL, A	IC, A	Y, Cм	YR, Cм	S, BA	cosφ
1	Ср	127	1,389	176.5	1.389	0.955	0,958	0,011	0,011	176,403	1
2	Ср+10	127	1,452	176.5	1.389	0.955	1,376	0,011	0,011	184,404	1
3	Ср+20	127	1,614	176.5	1.389	0.955	1,775	0,013	0,011	204,978	0,861
4	Ср-10	127	1,445	176.5	1.389	0.955	0,559	0,011	0,011	183,515	0,962
5	Ср-20	127	1,591	176.5	1.389	0.955	0,180	0,013	0,011	202,057	0,874

Y = I/U; Y_R = I_R/U; S = U∙I; cosφ = P/S.

Выводы.

Резонанс – явление в электрической цепи, содержащей индуктивные и емкостные элементы, при которых разность фаз напряжений и тока на входе электрической цепи равна 0.

1)

2) cosφ = P/S = 1

Коэффициент мощности равен отношению активной мощности к полной, и при резонансе равен 1.

3) S = P

Полная мощность равна активной, а индуктивная равна емкостной.

Q = Q_L – Q_C => Q_L = Q_C.

4) cosφ = G/Y = 1.

5) G = Y = Y_min.

B = B_L – B_C = 0 => B_L = B_C. Индуктивная проводимость равна емкостной.

6) I = U∙G = U∙Y_min = I_min.

При резонансе токов показания амперметра минимальные.

Задачи.

№ 2.27

Дано:	Решение:
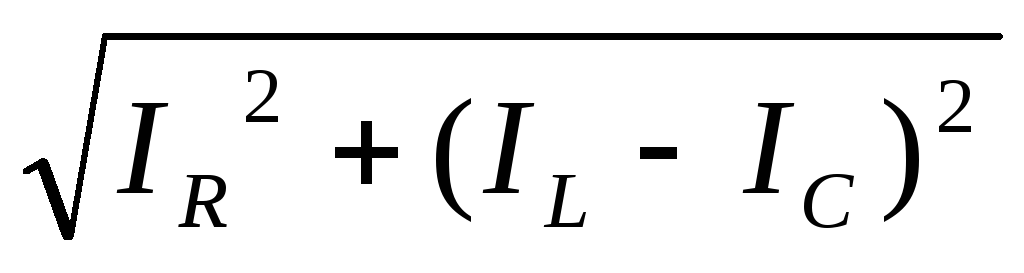
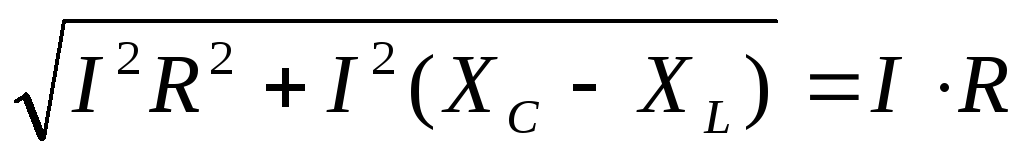
XL = XC = R = 20 Ом. U = 200 B.	I = IR + IC + IL. I = U = IR∙R + j∙IC∙XC - j∙IL∙XL = I∙R + j∙I∙(XC - XL). U = │U│ = I = .
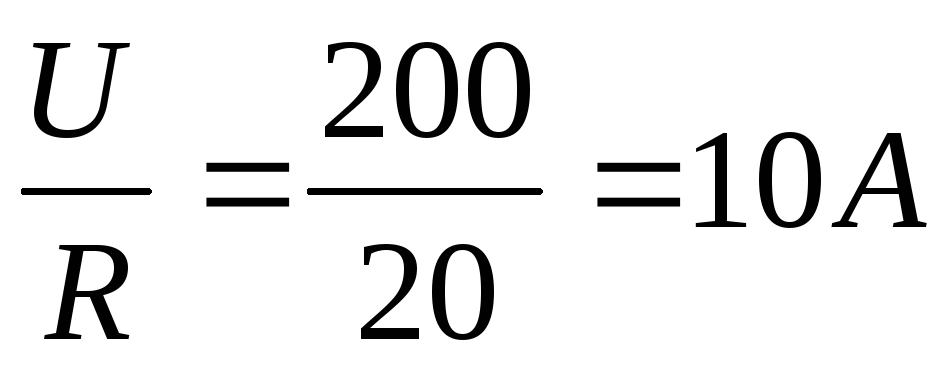Определить:
I - ?
XC = XL, U = I∙R,
Ответ: 10А.

№ 2.30

Дано:	Решение:
XC = XL = 100 Ом. R = 10 Ом. U = 120B.	I = IR + j∙IL - j∙IC. U = IR∙R + j∙IL∙XL - j∙IC∙XC = IR∙R + I∙j∙( XL – XC) XC = XL. U = │U│=I∙R I =
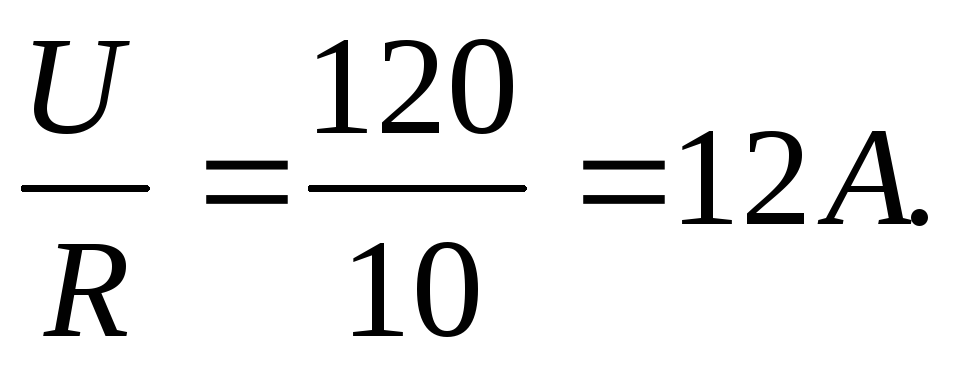
Определить:
I - ?
Ответ: 12А.

№2.42

Дано:	Решение:
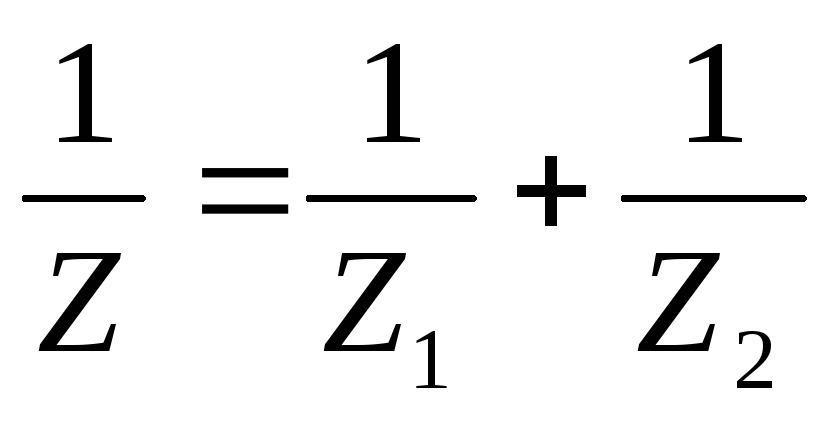
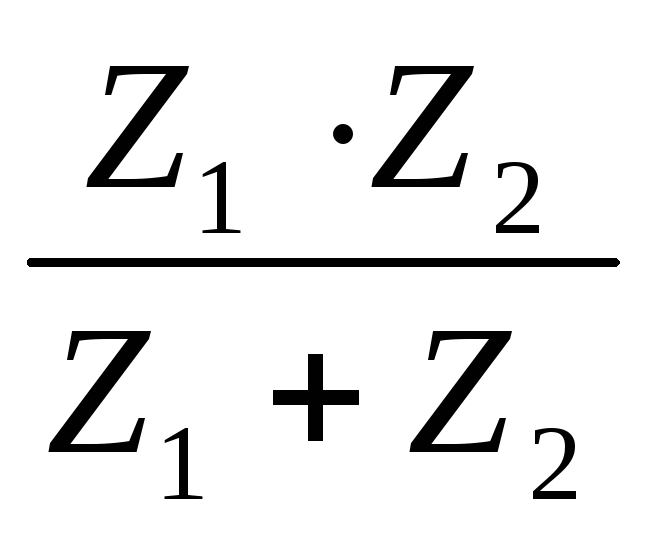
	Y = Y1 + Y2, Z = Z = 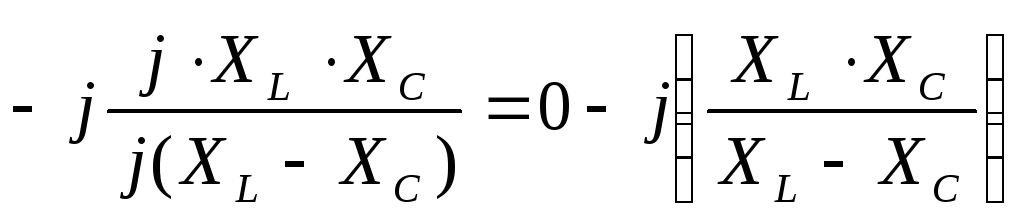, при XL = XC Z→ ∞.
Определить: полное сопротивление данной электрической цепи.(Z)
Z1 = jXL, Z2 = - jXC, Z = ,
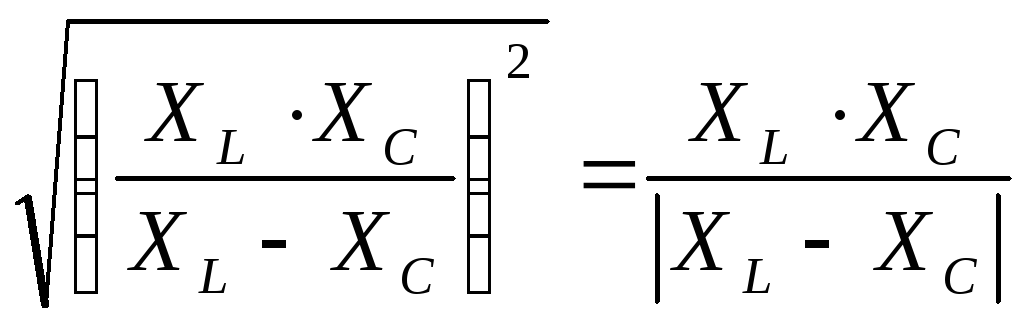Ответ: .
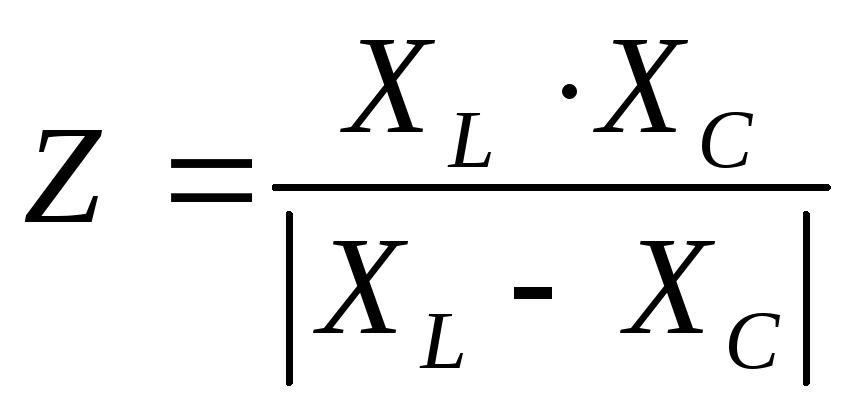