Методичка по физике / -5 Кинематика

1. КИНЕМАТИКА

	Это нужно понять и запомнить!
1.1. Основные законы и формулы

• Здесь и далее: векторы обозначены жирным шрифтом (r, v, a), а их модули и параметры задачи – обычным шрифтом – r, v, a, t. !

• Средняя и мгновенная скорости материальной точки:

, ,

, ,

где Δr – элементарное перемещение точки за время Δt; r − радиус-вектор точки; Δs − путь, пройденный точкой за время Δt.

• Путь, пройденный точкой:

• Среднее и мгновенное ускорения материальной точки:

, .

• Полное ускорение при криволинейном движении:

a = a_τ + a_n , ,

где − тангенциальная, а − нормальная составляющие ускорения (ρ – радиус кривизны траектории в данной точке)

• При равнопеременном движении:

, .

• Угловая скорость: .

• Угловое ускорение: .

• Угловая скорость для равномерного вращения:

,

где T – период вращения; n – частота вращения (n = N/t, где N – число оборотов, совершаемых телом за время t).

• Угол поворота и угловая скорость для равнопеременного вращения:

, ,

где ω₀ – начальная угловая скорость.

• Связь между линейными и угловыми величинами:

s = Rφ ; ; a_τ = Rε ; a_n = ω²R ,

где R – расстояние от оси вращения.

1.2. Примеры решения задач

1–1. Автомобиль проехал первую половину времени своего движения со скоростью v₁ = 54 км/ч, вторую поло­вину времени - со скоростью v₂ = 72 км/ч. Определите среднюю скорость движения автомобиля.

Решение:

Ответ: 63 км/ч.

1-2. Материальная точка движется вдоль прямой так, что ее ускорение линейно растет и за первые 10 с достигает значения 5/мс². Определите в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь.

Решение: a = kt, ,

Ответ: v₁ = 25 м/с; s₁ = 83,3 м.

1-3. Радиус-вектор частицы М относительно неподвижной точки О меняется со временем по закону r = Asinωt +Bcosωt, А и В – постоянные векторы, причем А _┴ В; ω – положительная постоянная. Найти ускорение а частицы и уравнение ее траектории y(x), взяв оси X и Y совпадающими по направлению с векторами А и В соответственно и имеющими начало в точке О.

Решение: Продифференцировав r по времени дважды, получим: т.е. вектор а все время направлен к точке О, а его модуль пропорционален расстоянию частицы до этой точки.

Найдем теперь уравнение траектории. Спроецировав r на оси X и Y, получим: откуда

Это уравнение эллипса с полуосями А и В соответственно.

1-4. Частице в момент времени t = 0 сообщили скорость v₀, после чего ее скорость стала меняться со временем t по закону v = v₀(1 – t/τ), где τ – положительная постоянная. Найти за первые t секунд движения: 1) вектор перемещения ∆r частицы; 2) пройденный ею путь s.

Решение: Так как dr = vdt = v₀(1 – t/τ)dt, то после интегрирования по времени от 0 до t, получим: ∆r = v₀t(1 – t/2τ).

Путь s, пройденный частицей за время t, равен где v – модуль вектора v. В соответствии с условиями задачи

Отсюда следует, что при t > τ интервал интегрирования необходимо разбить на две части: от 0 до τ и от τ до t. Интегрирование приводит к следующим результатам:

1-5. Трамвай движется прямолинейно от остановки А до следующей остановки В с ускорением, изменяющимся по закону a = a₀ –bs, где a₀ и b – положительные постоянные, s - расстояние от остановки А до трамвая. Найти расстояние между этими остановками и максимальную скорость трамвая.

Решение: Найдем сначала зависимость скорости от расстояния s. По определению dv = adt. С другой стороны, можно записать, что dt = ds/v, откуда vdv = (a₀-bs)ds. Проинтегрировав это выражение (от 0 до v слева и от 0 до s справа), получим

Отсюда видно, что расстояние между остановками, т.е. значение s₀, при котором v = 0, есть s₀ = 2a₀/b. Максимальную скорость найдем из условия dv/ds = 0, из которого следует, что при s_m = a₀/b.

1.3. Вопросы и задачи

1.01. Катер, двигаясь вниз по реке, обогнал плот в пункте A. Через τ = 60 мин после этого он повернул обратно и затем встретил плот на расстоянии l = 6 км ниже пункта A. Найти скорость течения, если при движении в обоих направлениях мотор катера работал одинаково.

1.02. Точка прошла половину пути со скоростью v₀. Оставшуюся часть пути она половину времени двигалась со скоростью v₁, а последний участок – со скоростью v₂. Найти среднюю за все время движения скорость точки.

1.03. Автомашина движется с нулевой начальной скоростью по прямому пути сначала с ускорением a = 5 м/с², затем равномерно и, наконец, замедляясь с тем же ускорением a, останавливается. Все время движения t = 25 с. Средняя скорость за это время ‹v› = 72 км/ч. Сколько времени автомашина двигалась равномерно?

1.04. Точка движется вдоль оси x со скоростью, проекция которой v как функция времени описывается графиком (см. рисунок.). Учитывая, что в момент t = 0 координата точки x = 0, начертить примерные графики зависимостей от времени ускорения a, координаты x и пройденного пути s . Рисунок к задаче 1.04

1.05. Две частицы 1 и 2 движутся с постоянными скоростями v₁ и v₂. Их радиус-векторы в начальный момент времени равны r₁ и r₂. При каком соотношении между этими четырьмя векторами частицы испытают столкновение друг с другом.

1.06. Два пловца должны попасть из точки A на одном берегу реки в прямо противоположную точку B на другом берегу. Для этого один из них решил переплыть реку по прямой AB, другой же – все время держать курс перпендикулярно к течению, а расстояние, на которое его снесет, пройти пешком по берегу со скоростью u. При каком значении u оба пловца достигнут точки B за одинаковое время, если скорость течения v₀ = 2 км/ч и скорость каждого пловца относительно воды v' = 2,5 км/ч?

1.07. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с².Через 2 с после начала подъема с потолка кабины стал падать болт. Найти время свободного падения болта.

1.08. Радиус-вектор частицы меняется со временем t по закону r = c·t(1 - αt), где c – постоянный вектор, α – положительная постоянная. Найти: а) скорость v и ускорение a частицы в зависимости от времени; б) промежуток времени Δt, по истечении которого частица вернется в исходную точку, а также путь s, который она пройдет при этом.

1.09. Частица движется в положительном направлении оси x так, что ее скорость меняется по закону v =(αx)^1/2, где α – положительная постоянная. Имея в виду, что в момент t = 0 она находилась в точке x = 0, найти: а) зависимость от времени скорости и ускорения частицы; б) среднюю скорость частицы за время, в течение которого она пройдет первые s метров.

1.10. Точка движется вдоль оси OX, причем координата x изменяется по закону х = а соs (2π/Т)t. Найти:

а) выражение для проекций на ось OX скорости v и ускорения a,

б) путь s₁, пройденный точкой за промежуток времени от t = 0 до t = Т/8,

в) путь s₂, пройденный точкой за промежуток времени от t = Т/8 до t = Т/4,

г) путь s, пройденный точкой за промежуток времени от t = 0 до t = Т.

1.11. Зависимость координат движения частицы от времени имеет вид х = аcosωt, у = аsin ωt, z = 0 (а и ω - константы).

а) Определить радиус-вектор r, скорость v и ускорение a частицы, а также их модули.

б) Вычислить скалярное произведение векторов r и v. Что означает полученный результат?

в) Вычислить скалярное произведение векторов r и a. Что означает полученный результат?

г) Найти уравнение траектории частицы.

д) В каком направлении движется по траектории частица?

е) Охарактеризовать движение частицы.

ж) Как изменится движение частицы, если в выражении для у изменить знак на обратный.

1.12. На лодке, имеющей скорость v₀, спускают парус в момент времени t₀, но лодка продолжает двигаться. Во время движения лодки без паруса произведены измерения ее скорости, которые установили гиперболическую зависимость скорости от времени (v ~ 1/t). Покажите, что ускорение лодки было пропорционально квадрату ее скорости.

1.13. Играет ли роль при прыжках в длину высота полета? Какие факторы определяют дальность прыжка?

1.14. Под каким углом к горизонту надо бросить тело, чтобы высота подъема была равна дальности полета?

1.15. Небольшое тело (материальная точка) брошено из точки О под углом α к горизонту с начальной скоростью v₀ (см. рисунок5). Пренебрегая сопротивлением воздуха, найти: а) время полета τ, б) дальность полета l, в) наибольшую высоту поднятия тела h, г) уравнение траектории тела в координатах x’, y’, д) значения |dv/dt| и d|v|dt в вершине траектории, е) радиус кривизны R траектории в точках О и О’.Точки бросания и падения считать лежащими на одном уровне.

Рисунок к задаче 1.15	Рисунок к задаче 1.16

1.16. С машины, идущей со скоростью v₀, на дорогу брошен мяч с горизонтальной скоростью u относительно машины u < v. Высота машины Н. По какой траектории будет двигаться мяч относительно дороги? Удары мяча о дорогу считать упругими.

1.17. С вышки одновременно с одинаковыми по модулю скоростями выбрасываются по всевозможным направлениям шарики. Как будут располагаться шарики в различные моменты времени относительно Земли?

1.18. Почему при просмотре кинокадров с движущимся автомобилем его колеса часто кажутся неподвижными или вращающимися с малой угловой скоростью?

1.19. Колесо радиусом R вращается против часовой стрелки с постоянной угловой скоростью ω. Укажите модуль и направление вектора ускорения для точки, находящейся на ободе колеса. Какой путь прошла эта точка, каково ее перемещение, чему равен модуль вектора средней скорости и средний модуль скорости, если колесо сделало полоборота, один оборот?

1.20. Точка движется, замедляясь, по прямой с ускорением, модуль которого зависит от ее скорости v по закону a = bv, где b − положительная постоянная. В начальный момент скорость точки равна v₀ . Какой путь она пройдет до остановки? За какое время этот путь будет пройден?

1.21. Из пушки выпустили последовательно два снаряда со скоростью v₀ = 250 м/с: первый – под углом α₁ = 60^o к горизонту, второй – под углом α₂ = 45^o (азимут один и тот же). Пренебрегая сопротивлением воздуха, найти интервал между выстрелами, при котором снаряды столкнутся друг с другом.

1.22. Частица движется с постоянной по модулю скоростью v по плоской траектории y(x). Найти ускорение частицы в точке x = 0 и радиус кривизны траектории в этой точке, если траектория имеет вид параболы y = ax² (a – постоянная).

1.23. Частица движется с постоянной по модулю скоростью v по плоской траектории y(x). Найти ускорение частицы в точке x = 0 и радиус кривизны траектории в этой точке, если траектория имеет вид эллипса (x/a)² + (y/b)² = 1. Здесь a и b − постоянные.

1.24. Твердое тело вращается с постоянной угловой скоростью ω₀ = 0,5 рад/с вокруг горизонтальной оси AB. В момент t = 0 ось AB начали поворачивать вокруг вертикали с постоянным угловым ускорением β₀ = 0,1 рад/с². Найти угловую скорость и угловое ускорение тела через t =3,5 с.

1.25. Свободно падающее тело в последнюю секунду своего падения проходит половину всего пути. Найти: 1) с какой высоты h падает тело; 2) продолжительность его падения.

1.26. Тело A брошено вертикально вверх с начальной скоростью v₁, тело B падает с высоты h с начальной скоростью v₂ = 0. Найти зависимость расстояния x между телами A и B от времени t, если известно, что тела начали двигаться одновременно.

1.27. Расстояние между станциями метрополитена 1,5 км. Первую половину этого расстояния поезд проходит равноускоренно, вторую – равнозамедленно. Максимальная скорость поезда 50 км/ч. Найти: 1) величину ускорения, считая его численно равным замедлению; 2) время движе­ния поезда между станциями.

1.28. Поезд движется со скоростью 36 км/ч. Если прекратить подачу пара, то поезд, двигаясь равнозамедленно, останавливается через 20 сек. Найти: 1) отрицательное ускорение поезда; 2) на каком расстоянии до остановки надо прекратить доступ пара?

1.29. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся на расстоянии 5 м от места бросания. Высота места удара на 1 м меньше высоты, с которой брошен мяч. С какой скоростью v₀ был брошен мяч? Сопротивление воздуха не учитывать.

1.30. Камень брошен горизонтально со скоростью v_x = 15 м/с. Найти нормальное и тангенциальное ускорения камня через 1 сек после начала движения. Сопротивление воздуха не учитывать.

1.31. Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота φ по закону ω = ω₀ – aφ, где ω₀ и a положительные постоянные. В момент времени t = 0 угол φ = 0. Найти зависимости от времени: а) угла поворота; б) угловой скорости.

1.32. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением a_τ = 5 см/с². Через сколько времени после начала движения нормальное ускорение a_n точки будет равно тангенциальному a_τ ?

1.33. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением a_τ = 5 см/с². Через сколько времени после начала движения нормальное ускорение a_n точки будет вдвое больше тангенциального?

1.34. Точка движется по окружности радиуса R = 20 см с постоянным тангенциальным ускорением a_τ = 5 см/с². Найти нормальное ускорение a_n через t = 20 сек после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v равна 10 см/с.

1.35. Определить, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося колеса, больше тангенциального ускорения для того момента времени, когда вектор полного ускорения этой точки со­ставляет угол 30^o с вектором ее линейной скорости.

1.36. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся на расстоянии 5 м от места бросания. Высота места удара на 1 м меньше высоты, с которой брошен мяч. Под каким углом φ мяч подлетает к поверхности стенки? Сопротивление воздуха не учитывать.

1.37. Под каким углом к горизонту надо бросить тело, чтобы высота подъема была равна: дальности полета? в два раза больше? в два раза меньше?

1.38. Найдите угловую скорость и нормальное ускорение при движении Земли по круговой орбите вокруг Солнца, Средний радиус земной орбиты R = 1,5∙10⁸ км. Найдите линейную скорость орбитального движения Земли.

1.39. Определите угловую скорость вращения Земли вокруг своей оси. Найдите нормальное ускорение и линейную скорость точек земной поверхности на географической широте φ. Радиус земного шара 6400 км.

1.40. Известно, что Луна обращена к Земле всегда одной и той же стороной. Почему это возможно? В каком отношении находятся угловые скорости вращения Луны вокруг своей оси ω₁ и вокруг Земли ω₂?

1.41. Шары центробежного регулятора Уатта, вращающегося вокруг вертикальной оси с угловой скоростью  = 10 рад/с, благодаря изменению нагрузки машины отходят от этой оси, имея для своих стержней в данном положении угловую скорость ₁ = 1,2 рад/с. Найти абсолютную скорость шаров регулятора в рассматриваемый момент, если длина стержней l = 0,5 м, расстояние между осями их подвеса 2e = 0,1 м, углы, образованные стержнями с осью регулятора, ₁ = ₂ =  = 30.

Рисунок к задаче 1.41	Рисунок к задаче 1.42

1.42. Наклонная плоскость АВ, составляющая угол 45 с горизонтом, движется прямолинейно параллельно оси Ox с постоянным ускорением 0,1 м/с². По этой плоскости спускается тело Р с постоянным относительным ускорением 0,1 м/с². Начальные скорости плоскости и тела равны нулю, начальное положение тела определяется координатами x = 0, y = h. Определить траекторию, скорость и ускорение абсолютного движения тела.

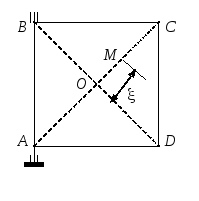
1.43. Прямоугольник АВСD вращается вокруг стороны CD с постоянной угловой скоростью  =  рад/с. Вдоль стороны АВ движется точка М по закону  = b sin  м. Даны размеры: DA = CB = b м. Определить величину абсолютного ускорения точки в момент времени t = 1 c.

Рисунок к задаче 1.43	Рисунок к задаче 1.44

1.44. Квадрат ABCD со стороной 2b м вращается вокруг стороны AB с постоянной угловой скоростью  = рад/с. Вдоль диагонали АС совершает колебание точка М по закону  = b cos  м. Определить величину абсолютного ускорения точки при t = 1 c и t = 2 c.

1.45. Полое кольцо радиуса r жестко соединено с валом АВ. Ось вала расположена в плоскости оси кольца. Кольцо заполнено жидкостью, движущейся в нем в направлении стрелки с постоянной относительной скоростью u. Вал АВ вращается по направлению движения стрелки часов, если смотреть по оси вращения от А к В. Угловая скорость вала  постоянна. Определить величины абсолютного ускорения частиц жидкости, расположенных в точках 1, 2, 3 и 4.

1.46. По условиям предыдущей задачи, измененным лишь в том отношении, что плоскость оси колеса перпендикулярна оси вала АВ, определить те же величины в двух случаях:

1) переносное и относительное движения имеют одно направление;

2) составляющие движения противоположны по направлению.

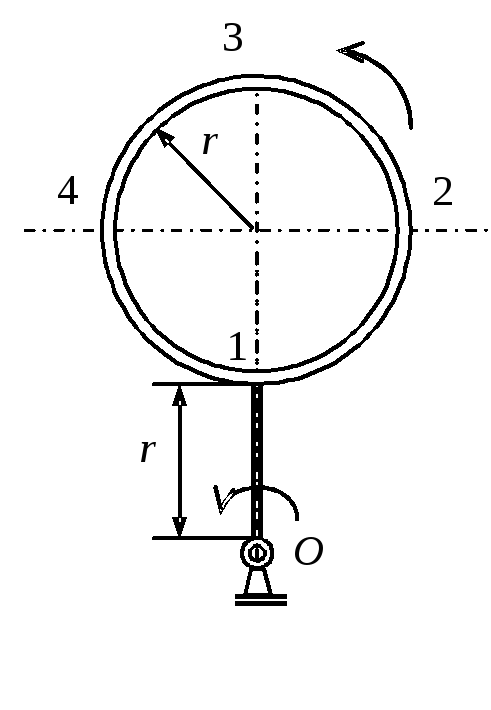
Рисунок к задаче 1.45	Рисунок к задаче 1.46

1.47. Точка М равномерно движется по образующей кругового конуса с осью ОА от вершины к основанию с относительной скоростью v_r, угол МОА = . В момент t = 0 расстояние ОМ_о = b. Конус равномерно вращается вокруг своей оси с угловой скоростью . Найти абсолютное ускорение точки М.

1.48. По железнодорожному пути, проложенному по параллели северной широты, движется тепловоз со скоростью v_r = 20 м/с с запада на восток. Найти величину кориолисова ускорения а_с тепловоза.

Рисунок к задаче 1.47	Рисунок к задаче 1.48

1.49. Река ширины 1км течет с юга на север со скоростью 1,5 м/c. Определить кориолисово ускорение а_с частиц воды, находящихся на 60 северной широты. Определить, у какого берега вода выше и насколько, если известно, что поверхность воды должна быть перпендикулярна направлению вектора, составленного из ускорения силы тяжести g и вектора, равного и противоположного кориолисову ускорению.

1.50. Диск радиуса R вращается с постоянной угловой скоростью ₁ вокруг горизонтальной оси О₁О₂, которая в свою очередь вращается с постоянным угловым ускорением _o вокруг вертикальной оси О₃О₄, имея в начальный момент t = 0 угловую скорость ₀. Найти скорости и ускорения точек А, В, С и D диска.

1.51. Ворот радиуса r = 0,1 м, вращаясь по закону  рад, приводит в движение посредством нерастяжимой нити каток радиуса R = 0,2 м, который катится без скольжения по грани треугольной призмы. Призма перемещается по горизонтальной плоскости по закону  м. Считая, что скольжение нити по вороту и катку отсутствует, определить в момент времени t = 0,5 c скорости и ускорения точек А, В и С, указанных на рисунке.

Рисунок к задаче 1.50	Рисунок к задаче 1.51

1.52. Диск вращается с постоянной угловой скоростью  вокруг оси, проходящей через его центр перпендикулярно плоскости диска. По хорде АВ из его середины D движется точка М с постоянной относительной скоростью u. Хорда отстоит от центра диска на расстоянии c. Найти абсолютные скорость и ускорение точки М как функцию расстояния x = DM.