Алгоритм декодирования Витерби.

Состояние сверточного кодера можно представлять с помощью графа, который называют решетчатой диаграммой (решетка). Решетчатую диаграмму используют:

1. для определения последовательности на выходе кодера V при заданной последовательности на входе кодера U (кодирование на передающей стороне);

2. для определения информационной последовательности U на выходе декодера на приемной стороне.

Отсюда появилось второе название сверточных кодов – треллис кодирование (trellis-code). Рассмотрим решетку для сверточного кода с кодовым ограничением N=3 и скоростью ½ (m=2).

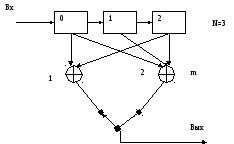
При построении решетчатой диаграммы кодер рассматривают как конечный автомат, текущее состояние которого зависит от предыдущего состояния и входного символа на данном такте работы.

Возможные состояния сверточного кодера изображают в виде вершин (узлов) решетки на вертикальных линиях, которые обозначают уровни обработки входной последовательности. То есть, на 1-й уровень попадаем после обработки первого информационного символа, на 2-й уровень – попадаем после обработки второго информационного символа и т.д. В технической литературе вертикальные штриховые линии на диаграмме обычно не показывают.

Таким образом, каждый уровень решетчатой диаграммы соответствует состоянию сверточного кодера после ввода очередного информационного символа. Число состояний кодера равно 2^N-1. В нашем примере – 4.

Состояния кодера определяются состоянием (N-1) левых (младших) ячеек памяти регистра сдвига.

От каждого узла предыдущего уровня отходят два ребра. Верхнее ребро соответствует поступлению на вход кодера символа «0», нижнее ребро соответствует поступлению на вход кодера символа «1».

Каждому ребру приписаны m двоичных символов, которые появляются на выходе кодера на данном такте работы.

В общем случае:

Число вершин (узлов) на каждом уровне решетки равно

2ⁱ, если i=0, …, (N-1).

Начиная с уровня (N-1), число вершин на каждом уровне равно 2^N-1.

Начиная с уровня N, структура диаграммы повторяется.

В нашем случае:

Число вершин на каждом уровне решетчатой диаграммы, начиная со второго (на рисунке показаны уровни 0 – 4) равно 2^N-1 =4, где N=3 – длина кодового ограничения, то есть число ячеек в регистре сдвига. Начиная с третьего уровня, структура диаграммы повторяется.

ОБЩЕЕ ПРАВИЛО ПОСТРОЕНИЯ РЕШЕТКИ

На каждом уровне входной символ 0 соответствует выбору верхнего ребра, а входной символ 1 – соответствует выбору нижнего ребра.

Каждый входной символ порождает на выходе кодера m (у нас ДВА) символа, приписанные соответствующему ребру.

Например, входная последовательность 1011

дает выходную последовательность 11 01 00 10.

Декодирование

Задача декодирования сверточного кода по алгоритму Витерби рассматривается как задача нахождения наиболее правдоподобного пути по решетчатой диаграмме с помощью некоторых правил. Это означает, что последовательность, образованная в результате движения по найденному пути, должна быть ближе всего к принятой последовательности. Другими словами декодер приемника пытается определить, по какому пути на решетчатой диаграмме изменялось состояние кодера в передатчике. Решение принимается в соответствии с принципом максимального правдоподобия.

Рассмотрим, как приемник восстанавливает информационную последовательность. Предположим, информационная последовательность представляет собой U=0 1 0 1 0 1 0 1…..

На выходе сверточного кодера появилась последовательность

V=00 11 01 00 01 00 01 00

На вход приемника поступила последовательность

Y=01 11 01 00 01 00 01 00 (ошибка во втором бите)

При нахождении наиболее правдоподобного пути по решетчатой диаграмме будем использовать понятие метрики пути – расстояние Хемминга (t) между принятой комбинацией и комбинацией, образованной при движении по определенному пути на диаграмме.

0 1

		t=1 (Путь по диаграмме дает 00 )	t-метрика пути
		t=1 (Путь по диаграмме дает 11 )	Уровень 1. Принято: 01

Накопленное значение метрики пути

			t=3 (Путь по диаграмме 00 00 )
			t=1 (Путь 00 11 )	Уровень 2. Принято: 01 11
			t=2 (Путь 11 01 )
			t=2 (Путь 11 10 )

Каждый из путей после уровня 2 раздваивается. Общее число путей стало равно 8.

Сравним метрики для пар путей, ведущих в каждую вершину уровня 3. В каждой паре сохраним только один путь – с лучшей (минимальной) метрикой. Оставшиеся пути называются выжившими.

0 1 2 3









t=3







t=3

Уровень 3. Принято: 01 11 01





t=1





t=2











t=3









t=1

Уровень 4. Принято: 01 11 01 00







t=3







t=3













T=4











T=4

Уровень 5. Принято: 01 11 01 00 01









T=1









T=3

И так далее…