Линейные коды

Блочным линейным кодом называется (n, k) код, проверочные символы которого являются линейными комбинациями информационных символов. Здесь:

n – длина кода, то есть длина кодовых слов

k – число информационных символов

Обозначим U – последовательность из k информационных символов.

U=(u₁, u₂,…….u_k)

Обозначим V – кодовое слово линейного кода длиной n символов.

V=(v₁, v₂,……….v_n)

К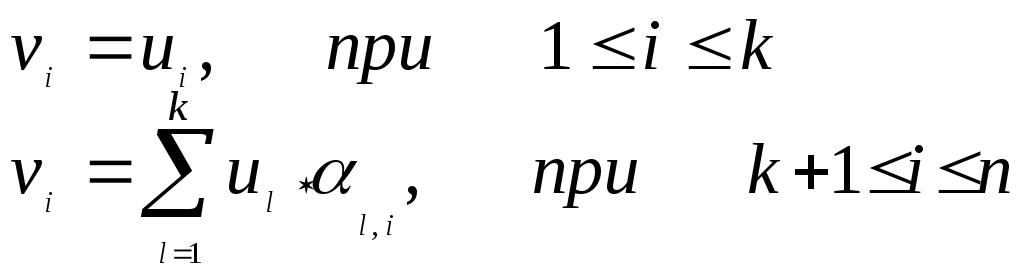одовое словоV формируется из информационной последовательности U по следующему правилу:

Коэффициенты _l,i представляют собой фиксированные двоичные символы, не зависящие от U .При выборе разных совокупностей _l,i получаются различные линейные коды.

Отношение R=k/n называется скоростью кода, а величина W=1-R – называется избыточностью кода.

Пример

Запишем в виде формул процедуру нахождения символов кодового слова для линейного кода с параметрами (5, 3), если задана некоторая информационная последовательность из трех символов U=(u₁,u₂,u₃). Кодовое слово будет содержать 5 символов V=(v₁,v₂,v₃,v₄,v₅).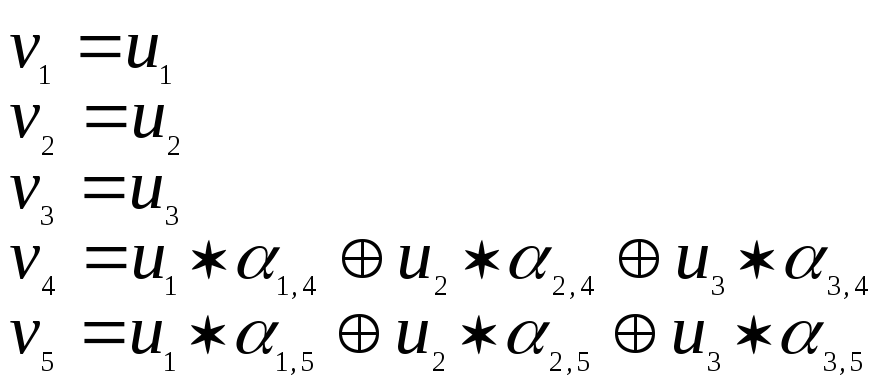

Линейный код может быть задан в виде полной таблицы кодовых слов или при помощи указания коэффициентов _l,i . Второй способ более экономичен.

При задании линейного кода с помощью набора коэффициентов _l,i записывается образующая матрица G . Матрица G имеет размер kxn .

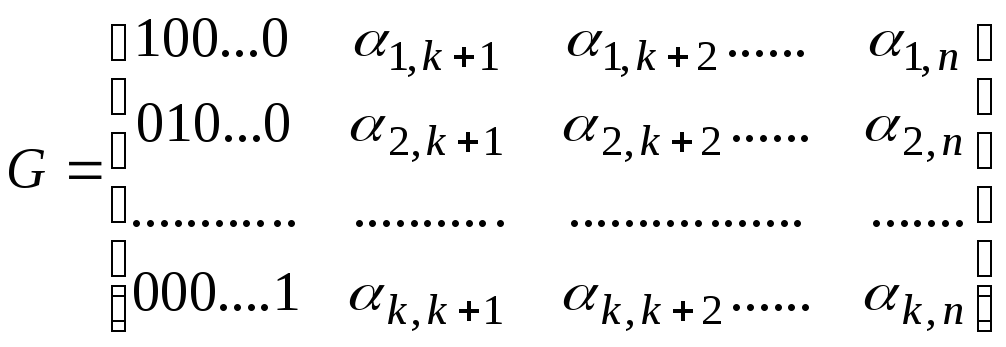
Первые k столбцов представляют собой единичную матрицу размером kxk , следующие n-k столбцов представляют совокупность коэффициентов _l,i (матрица проверочных элементов).

Это запись образующей матрицы в канонической форме.

Кодовая комбинация на выходе кодера канала равна произведению информационной последовательности на образующую матрицу линейного кода V=U×G.

Свойства линейных кодов

1. Любые к линейно-независимых кодовых слов задают все множество 2^к слов линейного кода.

К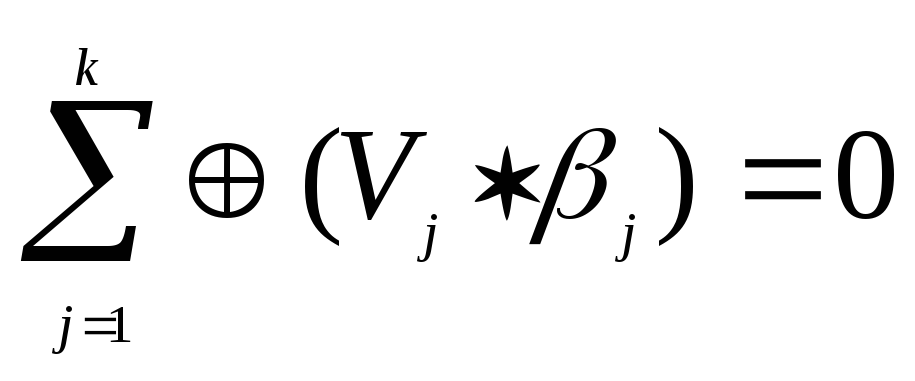одовые словаV_j являются линейно-независимыми, если сумма по модулю 2, приведенная ниже, равна 0 только, когда все двоичные коэффициенты _j равны 0.

Другими словами: суммирование любого числа кодовых слов из группы k линейно-независимых слов Vj не приводит к нулевому результату.

2. Сумма по модулю 2 любого числа кодовых слов также является словом данного линейного кода.

3. Нулевая последовательность всегда является кодовым словом.

4. Кодовое расстояние d_min равно минимальному весу ненулевого кодового слова.

5. Из любого линейного (n,k) кода с кодовым расстоянием d_min можно получить укороченный код (n-i, k-i) с кодовым расстоянием не меньше d_min.

Декодирование линейных кодов

Обозначим последовательность, поступающую с выхода дискретного канала на вход декодера Y. Процедура декодирования линейного разделимого кода сводится к проверке соотношения: принятые проверочные элементы кодовой комбинации совпадают с результатом вычисления этих элементов принимающей стороной? Для проверки этого соотношения декодер вычисляет синдром принятой последовательности.

Синдром S – это строка, которая содержит r=n-k элементов и представляет собой сумму  (по модулю 2) для каждого из r проверочных символов, вычисленных по принятым информационным символам, и r реально принятых проверочных символов.

Если ошибки в принятой комбинации отсутствуют, синдром равен нулю S=0 (все элементы синдрома равны 0). Если принятый j-й проверочный символ (1<=j<=r) отличается от i-го проверочного символа, вычисленного по принятым информационным символам по известным правилам, то j-й элемент синдрома будет равен 1.

Пусть e – комбинация или вектор ошибки. Вид синдрома зависит от вида вектора ошибки. Один и тот же синдром соответствует 2^k векторам ошибок.

Если , то вектор ошибки e' имеет тот же синдром, что и вектор e.

Синдром может быть вычислен с использованием проверочной матрицы Н.

S=Y×H.

Проверочная матрица имеет размерность n×r. Первые k строк проверочной матрицы представляют собой совокупность коэффициентов α_li, остальные r строк – это единичная матрица размером r×r.

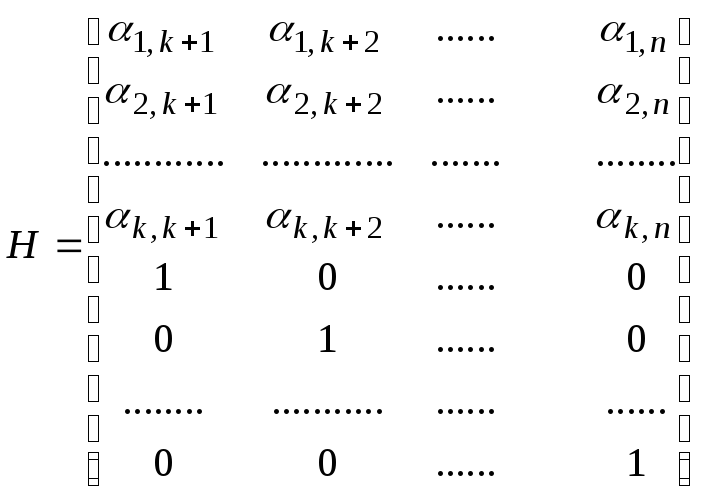
Д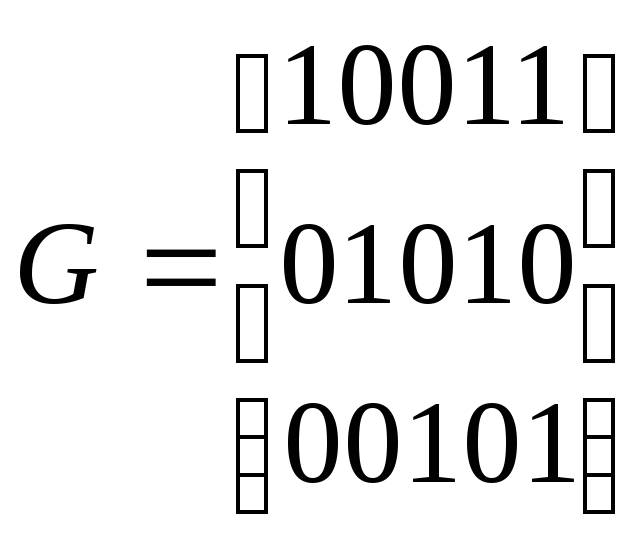ля кода (5,3) с образующей матрицейG

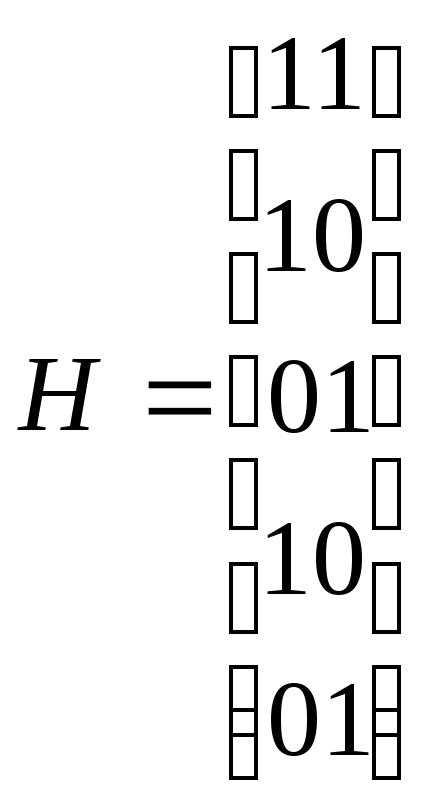проверочная матрица имеет вид

Декодирование с обнаружением ошибок

В данном случае при приеме последовательности Y вычисляется синдром S. Если S не равен нулю, выдается сигнал наличия ошибки. Если вектор ошибки e совпадает с одним из кодовых слов, ошибка не может быть обнаружена.

Определим вероятность необнаруженной ошибки при передаче комбинаций по каналу с независимыми ошибками (ДСК без памяти):

P(0/0)=P(1/1)=1-  - вероятность правильного приема двоичного символа в ДСК

P(0/1)=P(1/0)=  - вероятность ошибки в двоичном символе

Для ДСК без памяти вероятность появлениялюбого вектора ошибок веса t в кодовом слове длиной n символов равна

Линейный код не обнаружит ошибку, если вектор ошибки совпадет с каким-либо кодовым словом. Поэтому, для вычисления вероятности необнаруженной ошибки необходимо знать спектр весов кода. Спектром весов кода называется последовательность чисел N(t), каждое из которых показывает число кодовых слов, содержащих t единиц.

Декодирование с исправлением ошибок

При декодировании с исправлением ошибок каждому синдрому линейного кода ставят в соответствие определенный вектор ошибки, который является наиболее вероятным в заданном канале. Например, если задан двоичный симметричный канал без памяти ДСК, то в таблицу декодирования линейного кода следует включить вектора ошибок с минимальным весом.

Пример 1

Задан код с длиной кодового слова n=12. Определить необходимое минимальное число проверочных символов, если код должен исправлять все одиночные ошибки?

В соответствии с условием задачи число возможных одиночных ошибок в кодовом слове равно 12. Чтобы декодер работал в режиме исправления ошибок, необходимо чтобы каждому исправляемому вектору ошибки соответствовал свой синдром. Длина синдрома составляет (n-k) символов, число синдромов – 2^n-k. Число ненулевых синдромов должно быть не менее n=12. Следовательно, число проверочных символов должно быть не менее 4.

Пример 2

Задана матрица проверочных элементов _l,i линейного кода

• Я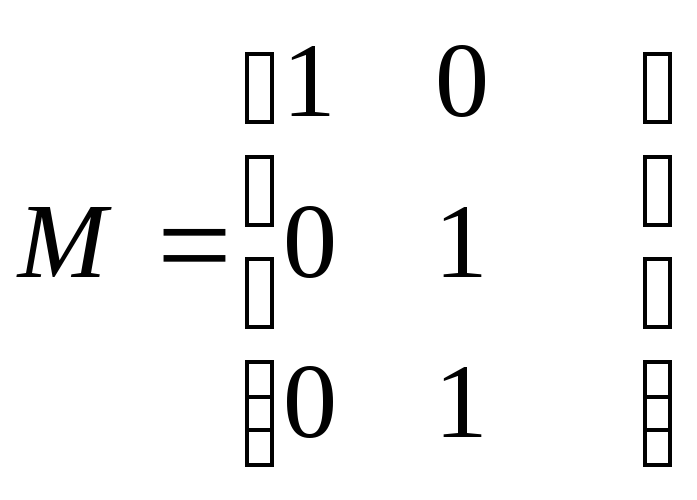вляются ли принятые последовательности кодовыми словами данного кода:

• 11110

• 01111

• 11010

• 11101

• 10100

• 00111

Поясните алгоритм решения.

• Определите кодовое расстояние заданного кода d_min и вес ошибок t, которые код гарантированно обнаруживает и исправляет.