4.15. Сопротивления при относительном движении твердого тела и жидкости

Сопротивление движению.

Пограничный слой

При движении твердого тела в вязкой жидкости или при обтекании его потоком возникает гидравлическое сопротивление со стороны жидкости. Твердые тела могут иметь разную форму и располагаться различно по отношению к набегающему потоку вязкой жидкости. Обтекание различных по форме тел обусловливает особенности их сопротивления. Тела в зависимости от условий обтекания подразделяют на хорошо и плохо обтекаемые. Каплевидное тело, пластина и диск, расположенные вдоль потока жидкости, являются хорошо обтекаемыми. Если же пластина или диск установлены поперек потока, то это плохо обтекаемые тела. Таким образом, сила сопротивления зависит от формы и размеров тела, а также от ориентации его по отношению к набегающему скоростному потоку.

Сопротивления, возникающие при обтекании тел потоком вязкой жидкости, можно разделить на сопротивления трения и сопротивления давления. В случае когда широкая пластина установлена вдоль набегающего потока, сопротивления будут определяться в основном сопротивлением трения, а для пластины, расположенной поперек (перпендикулярно) потока, - сопротивлением давления. Для хорошо обтекаемых тел сопротивление давления составляет примерно 25% сопротивления трения. Для плохо обтекаемых тел значение сопротивления давления может составлять % общего вязкостного сопротивления тела.

Сопротивления трения определяются касательными напряжениями, возникающими на поверхности тела. На поверхности тела при его обтекании жидкостью образуется пограничный слой малой толщины . Считается, что это тонкий слой жидкости, прилегающий непосредственно к обтекаемой поверхности тела, в пределах которого скорость изменяется от нуля на поверхности до скорости, составляющей около% скоростинабегающего невозмущенного, т.е. в отсутствие тела, потока. Толщина пограничного слоя много меньше характерного размера тела().

Величина силы трения зависит от режима течения в пограничном слое и от физических процессов, происходящих в нем. Режим течения в пограничном слое может быть ламинарным, турбулентным и смешанным. Он зависит от размеров шероховатости поверхности, температуры потока и поверхности тела, числа Рейнольдса

(4.159)

где - кинематическая вязкость.

При небольшой скорости набегающего потока жидкости течение в пограничном слое происходит в виде малых отдельных слоев, которые не смешиваются друг с другом. Частицы жидкости находятся в пределах этих слоев, вращаясь вокруг своих осей, перпендикулярных плоскости слоя, и они не перемещаются в поперечном направлении. Такой пограничный слой называется ламинарным. В этом случае шероховатость поверхности тела не влияет на сопротивление трения, так как имеет место плавное обтекание выступов шероховатости и не наблюдается образования вихрей.

При увеличении скорости потока в пограничном слое происходит перемещение частиц в поперечном направлении и их беспорядочное завихрение. Такой слой называется турбулентным пограничным слоем.

Ламинарный слой становится турбулентным при определенном значении числа Re, которое называется критическим числом Рейнольдса - .

Толщина пограничного слоя вдоль обтекаемой поверхности тела возрастает, причем значительно быстрее, если :

(4.160)

где - положение точки на теле, где ламинарный слой переходит в турбулентный.

При турбулентном режиме шероховатость поверхности влияет на течение в пограничном слое. Выступы шероховатости способствуют вихреобразованию и срыву с них вихрей. Отрыв вихрей, а значит, и пограничного слоя от поверхности приводит к образованию зоны отрыва, в которой возникают достаточно большие вихри.

Сопротивление давления (формы) обусловлено разностью давлений на лобовую и тыльную стороны поверхности обтекаемого тела, и сила давления равна равнодействующей этих сил. Соотношение формы и поверхности тела обусловлено отрывом пограничного слоя от поверхности. Точка на поверхности тела, в которой начинается отрыв пограничного слоя, называется точкой отрыва. Отрыв пограничного слоя приводит к образованию отрывного вихревого течения за телом. Изменение течения в пограничном слое связано с тем, что происходит резкое перемещение точки отрыва пограничного слоя от поверхности тела.

В результате перехода ламинарного пограничного слоя в турбулентный и возникновения поперечных пульсаций происходит резкое изменение сопротивления трения и давления, которое получило название «кризис сопротивления». Это относится к плохо обтекаемым телам. Давление на тыльную сторону тела зависит от расположения точки отрыва и ширины зоны отрыва пограничного слоя.

Установлено, что для хорошо обтекаемых тел (например, удлиненные по отношению к набегающему потоку тела) может не наблюдаться отрыва пограничного слоя от поверхности тела. Сопротивление давления для этих тел зависит от режима течения в пограничном слое и выражается следующей зависимостью:

, (4.161)

где - коэффициент сопротивления давления; - площадь миделевого сечения обтекаемого тела (площадь проекции тела на плоскость, перпендикулярную направлению движения);- плотность жидкости.

В случае больших чисел Рейнольдса коэффициент сопротивления давления, который является безразмерной величиной, зависит только от формы тела. В табл. 4.4 приведены значения для некоторых часто встречающихся на практике обтекаемых тел в зависимости от числа Рейнольдса. Для шара характерный размер равен его диаметруd.

Сопротивление трения записывается в следующем виде:

, (4.162)

где - коэффициент сопротивления трения; - площадь обтекаемой поверхности тела.

При обтекании пластины, установленной по направлению движения потока жидкости, в случае ламинарного пограничного слоя коэффициент определяется по формуле Блазиуса:

. (4.163)

Таблица 4.4 - Зависимость коэффициента от Re

Форма тела	Re
Шар		0,47
		0,22
Круглый цилиндр:
		1,2
		0,35
Круглый цилиндр при обтекании в направлении его оси:
		0,91
		0,85
		0,87
		0,99

При определении числа Re характерный размер равен длине пластины.

В случае турбулентного пограничного слоя для пластины длиной с эквивалентной шероховатостью поверхности(А.Альтшуль)

. (4.164)

В общем случае суммарное сопротивление предлагается определить по формуле, предложенной еще Ньютоном:

, (4.165)

где - коэффициент лобового сопротивления.

Коэффициент зависит от формы обтекаемого твердого тела, числа Рейнольдса и интенсивности турбулентности потока жидкости или газа.

Для тела в виде шара при числах

. (4.166)

А в случае, если , рекомендуется определять по формуле Озеена:

. (4.167)

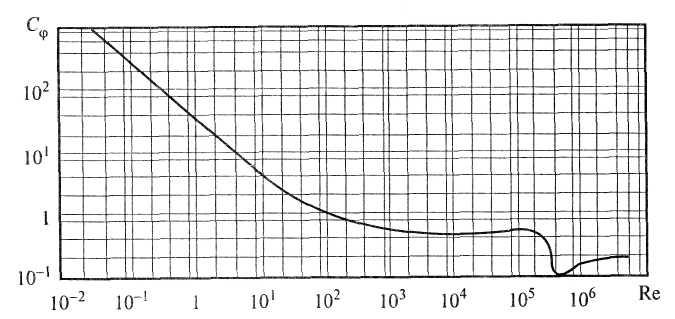
Рис. 4.27. Коэффициент сопротивления шара

В результате проведения экспериментальных исследований для шара были получены данные о зависимости от Re, они представлены на рис. 4.27.

Осаждение (всплывание) твердых частиц в покоящейся жидкости

Падение (осаждение) твердых тел в покоящейся жидкости может быть:

• свободное, когда на падающее тело не оказывают влияния соседние твердые тела и стенки емкости, в которой происходит осаждение;

• стесненное, когда, наоборот, на осаждение тела влияют соседние тела и стенки емкости;

• стесненное однородных по крупности, плотности и форме частиц;

• стесненное неоднородных частиц.

Движение твердых частиц при осаждении в покоящейся или сравнительно медленно движущейся жидкости является, как правило, равномерным. Скорость равномерного движения твердой частицы в достаточно большом объеме покоящейся жидкости (свободное осаждение) получила название гидравлической крупности .

Возьмем твердую частицу сферической формы диаметром d и массой , которая осаждается в большом объеме воды. Применительно к движущейся частице можно написать уравнение равновесия

, (4.168)

где ; G - сила тяжести частицы с учетом ее взвешивания в воде; F - сила полного сопротивления движению (сила лобового сопротивления).

В связи с тем что движение считается равномерным, ускорение частицы равно нулю: . Следовательно, можно написать:G = F.

Вес частицы сферической формы с учетом архимедовой силы

, (4.169)

где - плотность твердой частицы;- плотность воды.

Силу лобового сопротивления при падении частицы определим по формуле (4.169)

(4.170)

где - скорость равномерного движения частицы в воде.

Приравняв значения этих сил и сделав некоторые преобразования, получим значение гидравлической крупности, зависящее от коэффициента лобового сопротивления :

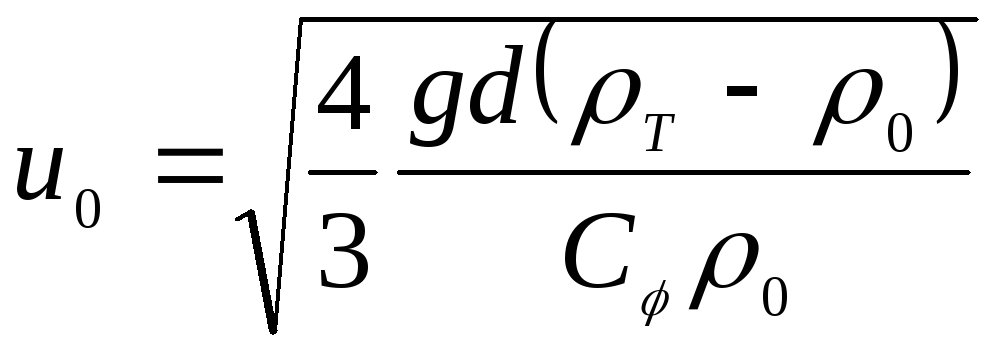. (4.171)

В случае когда , будет происходить всплывание частиц, и скорость всплывания

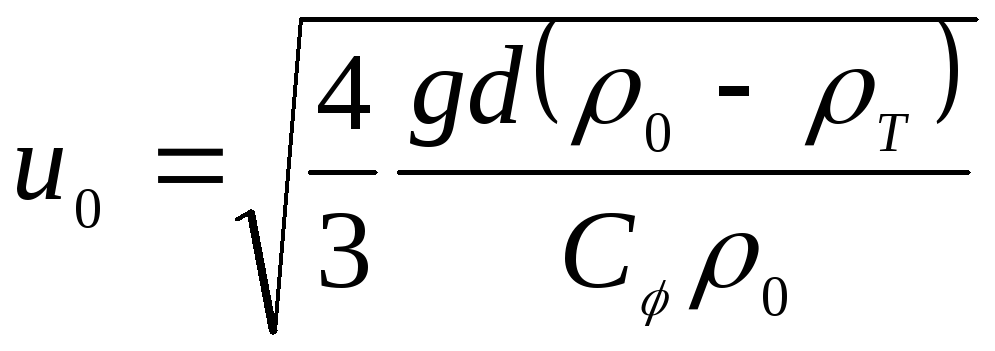(4.172)

Однако недостатком формул (4.171) и (4.170) является присутствие в них коэффициента лобового сопротивления , имеющего сложные зависимости от числа Рейнольдса и ряда других факторов.

При движении весьма малых частиц (Re<1) уравнение (4.171) в соответствии с равенством приобретает вид уравнения Стокса:

. (4.173)

Некоторая степень неточности при определении имеет место в связи с тем, что частицы имеют форму, несколько отличную от сферической. Поэтому берется осредненное значение диаметра частицы, т.е. эквивалентный ее диаметр

, (4.174)

где - объем твердой частицы, который соответствует объему шара диаметром.