4.13. Простые и сложные местные сопротивления

Внезапное сужение трубы

Гидравлические потери напора, как и при внезапном расширении, связаны с отрывом потока от стенок как в широкой, так и в узкой части трубы с образованием вихрей (водоворотной области) (рис. 4.19). При достижении потоком жидкости острых кромок узкой части трубы происходит отрыв потока, в результате он сужается (сечение С-С) и далее расширяется. Пространство вокруг суженного потока будет представлять собой вихревую область.

Между водоворотной областью и транзитным потоком образуется поверхность раздела. В результате пульсации скоростей и вихреобразования происходит массообмен частицами водоворотной области и самого потока.

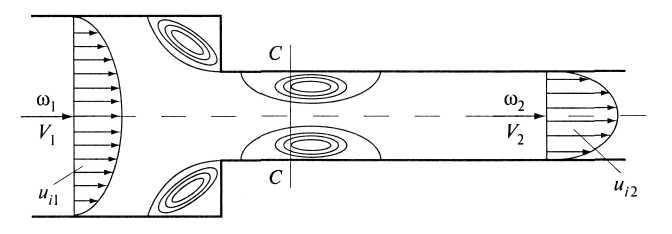
Рис. 4.19. Внезапное сужение трубы

Потери напора можно определить, используя формулу Борда, полагая, что в основном потери будут за сжатым сечением, а до сжатого сечения потери напора существенно малы.

Скорость в сжатом сечении С-С площадью

. (4.136)

Выразим отношение площадей сжатого сечения и площади узкой части трубы через коэффициент, который называется коэффициентом сжатия:

. (4.137)

Потери напора по Борда

. (4.138)

Из уравнения неразрывности

, . (4.139)

Выразим потери напора через скоростной напор :

(4.140)

или

. (4.141)

Тогда коэффициент местного сопротивления

. (4.142)

Коэффициент сжатия зависит от отношения площадей узкой и широкой трубы:. Отношение площадей.

Коэффициент может быть вычислен по формуле А. Альтшуля

. (4.143)

Коэффициент местных сопротивлений может быть определен по формуле, предложенной И. Идельчиком:

. (1.144)

Если , в случае когда труба выходит из большого резервуара,, тогда при прямых углах соединения трубы.

Вход потока в трубу

Экспериментальными исследованиями установлено, что сопротивления зависят от толщины передней кромки круглой трубы. Для кромки с относительной толщинойкоэффициент местных сопротивлений на входе. При бесконечно малой толщине кромки () .

Для уменьшения сопротивления на входе применяются входные наконечники конической формы или с плавным входом (рис. 4.20). В случае наличия перед входом в трубу экрана потери увеличиваются. В таких наконечниках весьма существенно уменьшается отрыв потока от стенок. Для конусных наконечников с , наконечников с плавным входом -при.

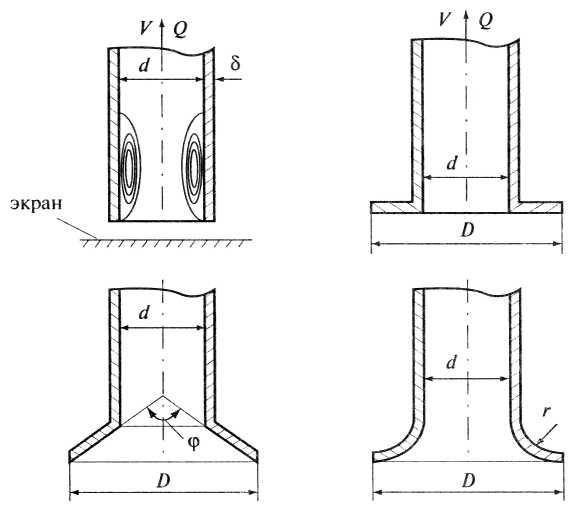
Рис. 4.20. Различные входы в трубу

Диафрагма на трубопроводе

Диафрагма устанавливается на трубопроводе для регулирования расхода воды в определенном месте. Трубопровод в месте установки диафрагмы имеет постоянное живое сечение, d=const (рис. 4.21).

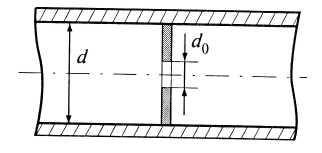
Рис. 4.21. Диафрагма на трубопроводе

Коэффициент местного сопротивления диафрагмы определяется по формуле

, (4.145)

где - отношение площади отверстия диафрагмы диаметром к поперечной площади сечения трубы диаметром ; - коэффициент сжатия при прохождении потока через отверстие диафрагмы, рекомендуется находить по формуле А. Альтшуля (4.143):

.

Закругление трубы

Плавно закругленные трубы или поворот трубы называют отводом. Радиус кривизны R влияет на вихреобразование потока жидкости, т.е. на сопротивление движению (рис. 4.22). Известна формула Вейсбаха по определению коэффициента местных сопротивлений при соблюдении следующих условий: :

, (4.146)

где - угол закругления.

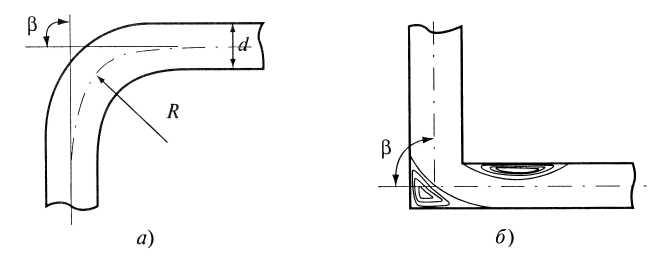
Рис. 4.22. Закругления труб: а - плавное закругление (отвод); б - резкое закругление

В случае резкого поворота трубы (рис. 4.22, б) возникают существенно большие потери напора. В результате действия центробежных сил происходит отрыв от стенок потока жидкости с вихреобразованием, приводящий к возникновению водоворотной области.

Для такого круглого колена коэффициент зависит от угла наклона осей колена . При находится в пределах значения 1,0. В случае большой шероховатости стенок будет больше единицы.

Регулирующая арматура

Задвижка. Для односторонней задвижки круглой трубы сопротивление зависит от степени ее открытия, т.е. от отношения (рис. 4.23). В результате малого открытия происходит отрыв потока от сегмента задвижки и стенок с образованием водоворотной области, а на поверхности раздела области с потоком происходит пульсация скоростей и интенсивное вихреобразование, приводящее к массообмену частицами жидкости.

В табл. 4.2 приведены значения коэффициента в зависимости от степени открытия .

Таблица 4.2 - Значения в зависимости от степени открытия

	0	0,125	0,25	0,375	0,5	0,625	0,75	0,875	1
	0,05	0,07	0,26	0,80	2,10	5,50	17,0	98

Рис. 4.23. Задвижка

Пробковый кран, вентили. Сопротивление пробкового крана напрямую зависит от угла открытия крана (рис. 4.24).

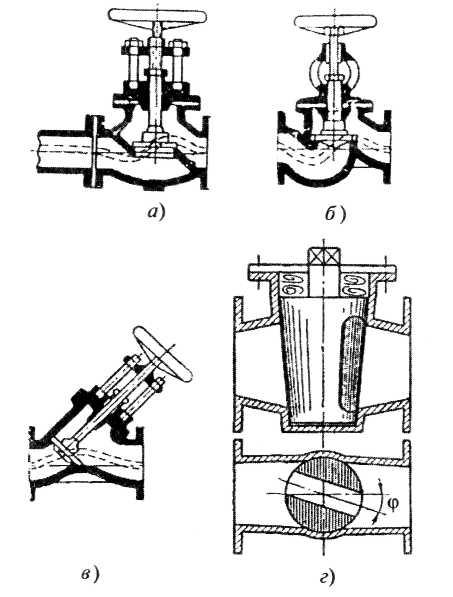
Рис. 4.24. Регулирующая арматура:

а - прямоточный вентиль; б - нормальный вентиль;

в - вентиль типа косва; г - пробковый кран

В табл. 4.3 приведены значения коэффициента местных сопротивлений крана .

Таблица 4.3 - Значения в зависимости от угла открытия

	10	20	30	40	50	60	65
	0,29	1,56	5,47	17,3	52,6	206	486

Значения коэффициентов местных сопротивлений вентилей (см. рис. 4.24) различной конструкции при полном их открытии следующие:

прямоточный - ;

нормальный - ;

с косым затвором (косва) - .

Тройники

Деталь трубы, в которой имеет место разделение или соединение потоков жидкости, называется тройником (рис. 4.25). При определении гидравлических потерь в тройниках принимается средняя скорость соответствующая расходудо разделения и - после слияния.

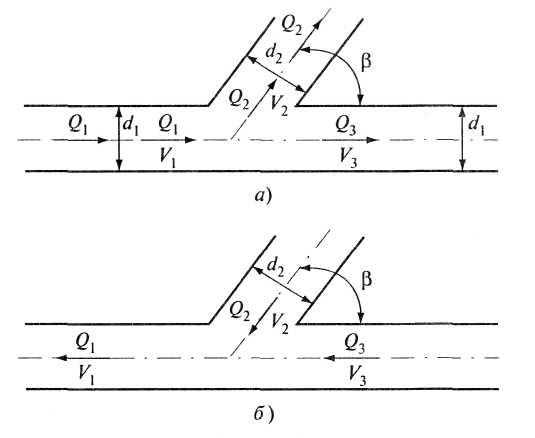
Рис. 4.25. Тройник: а - разделение потока; б - слияние потоков

Гидравлические потери напора возникают в результате соединения потоков жидкости или их разделения. Коэффициенты местных сопротивлений зависят от геометрии тройника, т.е. от угла , соотношения диаметров,, и отношения расходов и .

Коэффициенты местных сопротивлений , получены в результате многочисленных опытов, их значения приведены в специальных справочниках [2, 4].

♦ Пример 4.5

В трубопроводе диаметром мм имеется внезапное сужение диаметроммм. Определить местные потери напора и коэффициент, отнесенный к узкой части трубопровода. Расход воды в трубопроводе м³/с (см. рис. 4.19).

Коэффициент местных сопротивлений находим по формуле И. Идельчика (4.144):

.

Отношение площадей живых сечений характеризуется величиной .

,

.

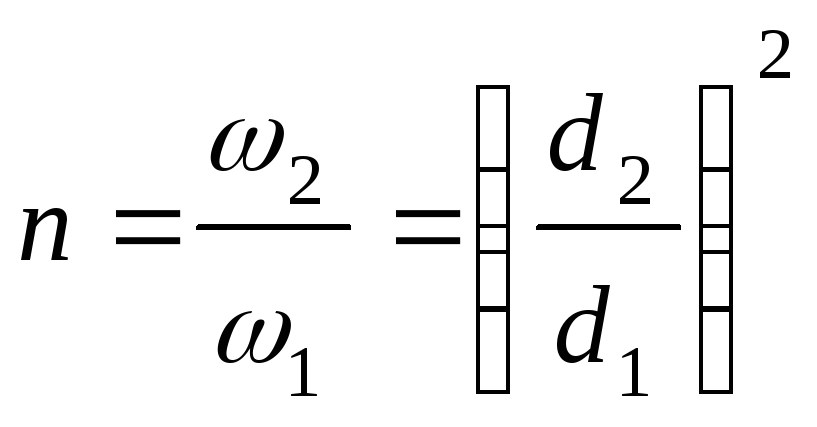Средняя скорость в сужающей части трубы диаметром мм/с.

Потери напора

м.

♦ Пример 4.6

Для ограничения расхода воды в трубопроводе диаметром мм установлена диафрагма. Избыточные давления до диафрагмы и после нее постоянны и соответственно равныкПа икПа. Определить необходимый диаметр отверстия диафрагмыd при условии, что расход м³/с (см. рис. 4.21).

Потери напора на участке трубопровода, где установлена диафрагма, при скорости в трубопроводе равны

м.

Средняя скорость в трубопроводе

м/с.

Коэффициент местных сопротивлений диафрагмы согласно формуле Вейсбаха

.

Коэффициент вычисляется по формуле А. Альтшуля (4.145)

.

Коэффициент сжатия потока (4.143)

,

.

В первом приближении примем .

Преобразуем формулу (4.145) для определения :

; ;

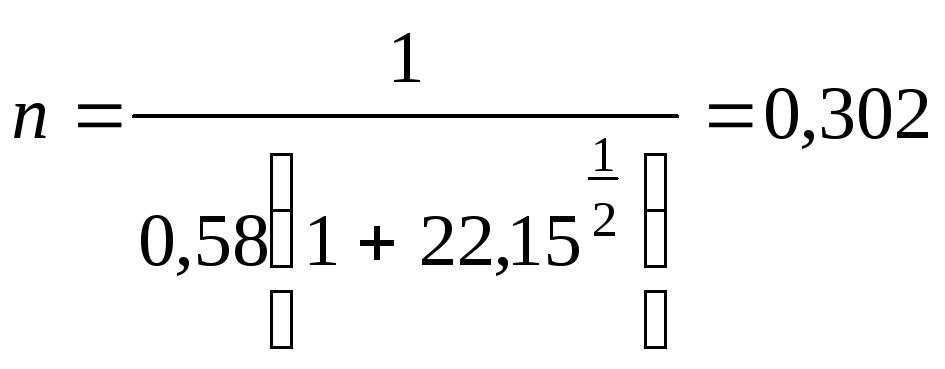мм.

Уточним полученный диаметр отверстия, вычислив :

;

.

Диаметр отверстия диафрагмы после уточнения

мм.