4.11. Местные гидравлические сопротивления

К местным гидравлическим сопротивлениям относятся различные устройства и элементы, устанавливаемые на трубопроводах, в которых происходит нарушение нормального движения потока в результате его деформации с изменением направления и значения средней скорости и возникновением вихреобразования. В результате деформации турбулентного потока происходит интенсивное перемешивание частиц и обмен количеством движения между частицами жидкости.

К элементам и устройствам относятся фасонная и трубопроводная арматура: отводы (колена), переходники, тройники, крестовины, диафрагмы, сетки, запорные регулирующие вентили (краны), задвижки, затворы, предохранительные и регулирующие клапаны, всасывающие наконечники, устанавливаемые на входе в трубу насосов, и т.д.

Самые простые местные гидравлические сопротивления можно разделить по направлению вектора средней скорости.

1. Скорость переменна при неизменном направлении движения потока жидкости.

Например, расширение трубы (русла) может быть плавное или внезапное; сужение трубы (русла) - плавное или внезапное.

2. Скорость постоянна при изменении направления движения потока.

Например, поворот трубы (русла) в виде плавного или резкого (рис. 4.15).

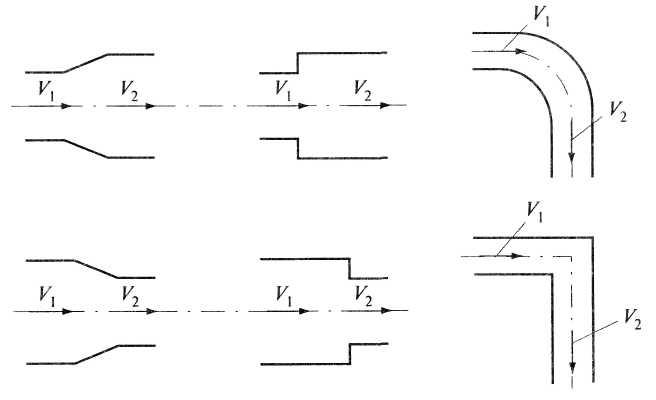
Рис. 4.15. Простейшие местные сопротивления

К более сложным местным сопротивлениям относятся сопротивления, в которых вектор скорости изменяется по значению и направлению, а также при слиянии или разделении потоков. Например, задвижки, клапаны, вентили и т.д., а также тройники, крестовины (рис. 4.16).

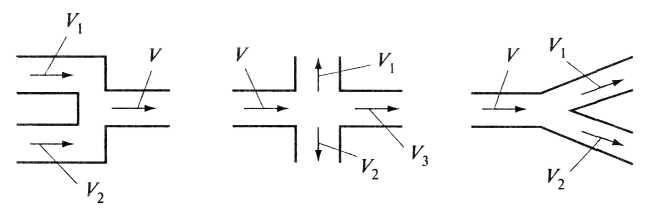
Рис. 4.16. Сложные местные сопротивления

В таких сопротивлениях в результате резких изменений направления и скорости происходит весьма значительная деформация потока с возникновением интенсивного вихреобразования.

Наибольшие вихреобразования возникают в сопротивлениях, имеющих какую-либо преграду. В результате обтекания преграды, находящейся в трубе, потоком жидкости происходит отрыв части потока от стенки трубы с возникновением вихревой зоны, которую называют водоворотной областью. Между водоворотной областью и основным потоком благодаря поперечным пульсационным скоростям происходит интенсивный обмен частицами жидкости на участке длиной в данной области. В результате массообмена частицами в районе поверхности русла имеет место увеличение пульсации и возникновение вихрей, перемещающихся непрерывно. По мере удаления от местного сопротивления эпюра скоростей выравнивается. Выравнивание эпюры скоростей в зависимости от формы и размеров преграды происходит на расстоянии(d - диаметр трубы).

Местные потери напора связаны непосредственно с типом местного сопротивления.

Местными потерями напора называют затраты удельной механической энергии, обусловленные работой сил трения и вихреобразованием на преодоление потоком жидкости местного сопротивления. На поддержание вихрей в определенной зоне затрачивается энергия потока.

Потери напора оцениваются через значение скоростного напора и обозначаются как. Вейсбах предложил местные потери напора определять по формуле

,

где - безразмерный коэффициент, называемый коэффициентом местного сопротивления; V - средняя скорость в живом сечении, как правило, непосредственно за местным сопротивлением.

Коэффициент , показывает количество скоростного напора, затрачиваемого на преодоление какого-либо местного сопротивления. В местном сопротивлении потери механической энергии при движении потока через него превращаются в тепловую энергию.

Коэффициент местных сопротивлений зависит:

• от формы и геометрических размеров;

• шероховатости внутренней поверхности сопротивления;

• режима движения.

В общем виде коэффициент , можно представить в следующем виде:

, (4.114)

где В - безразмерный коэффициент, зависящий от вида местного сопротивления при ламинарной и переходной области сопротивления; Re - число Рейнольдса; - коэффициент местных сопротивлений для квадратичной области, т.е. не зависящий от Re.

Для квадратичной области сопротивления Обычно при гидравлических расчетах принимается .

Коэффициент , находится опытным путем, а значения для различных местных сопротивлений, В приводятся в гидравлических справочниках.

Местные потери напора можно выразить в виде эквивалентной длины трубы . Местные потери напора принимаются равными потерям напора по длине,:

; ,

тогда

и . (4.115)

Потери напора по длине можно представить через коэффициент сопротивления по длине

. (4.116)

♦ Пример 4.3

Определить эквивалентную длину местного сопротивления в трубопроводе диаметром d=100 мм из новых стальных труб. Коэффициент местного сопротивления вентиля . Расход водыQ=16 л/с при t=20 °С.

Гидравлические потери по длине трубопровода согласно формуле Вейсбаха-Дарси

Местные потери напора в вентиле

Потери равны , тогда эквивалентная длина

Коэффициент гидравлического трения . Эквивалентную шероховатость новой стальной трубы принимаем мм (см. табл. 4.1).

Средняя скорость в трубе

Кинематическая вязкость воды (t=20 °С) м²/с.

Число Рейнольдса

.

Определим область сопротивления движения воды. Отношение

.

- область доквадратичного сопротивления.

.

Для данной области сопротивления коэффициент гидравлического трения вычисляется по формуле Альтшуля:

.

Эквивалентная длина

м.