Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Reshenie_S4_Dopolnenie_k_teorii

.pdf

Скачиваний:

Добавлен:

10.03.2016

Размер:

1.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

AM			2	AC 8,	BM			2	BC 12.	Далее
	1					2
		3					3
применить теорему косинусов для угла											A в
треугольнике ADM1 и							для угла B			в	тре-
угольнике DBM2 .

70. (МИЭТ, 2000). Два равнобедренных треугольника ABC и AMH, расположены так, что стороны АВ и АМ образуют угол в 45 . Угол при вершине A в каж-


дом треугольнике – прямой.					Известно,
		M2	что площадь пересече-
B			ния	треугольников
		M	равна 49, а площадь их

	M1	E	объединения		равна
		F	213.	Найдите площадь
			каждого из		треуголь-
A		D C	ников.
			Ответ:		SABC 100;
	H1
		H	SAMH	162 (рис. 32) или

			SABC 162; SAMH 100 .
		H2
			Указание. См. упраж-
	Рис. 32		нение 92.
		Дан равнобедренный треугольник
	71.
АВС,		AB BC 13 и		AC 10. Парал-

лельно боковым сторонам треугольника на одинаковом расстоянии от них проведены прямые. Найдите это расстояние, если площадь треугольника, образованного этими прямыми и основанием, лежащим на прямой АС, равна 15.

Ответ: 30 или 90 . Указание. См. «По-

13 13

собие», пример 27.

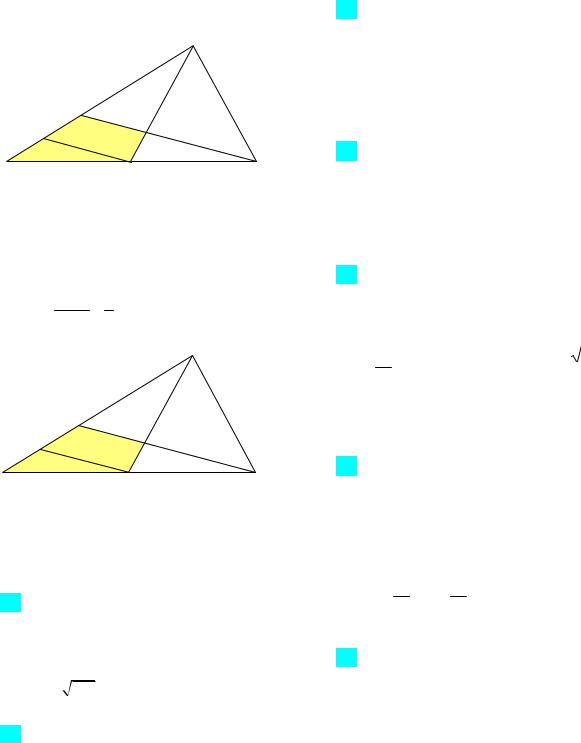
72. Дан правильный треугольник АВС площади 25. Параллельно его сторонам на равном расстоянии от них проведены три прямые, пересекающиеся внутри треугольника и образующие в пересечении треугольник A1B1C1 площади 4. Найдите

расстояние между параллельными сторонами треугольников АВС и A1B1C1 .


Ответ: 4		74	3	. Указание. 1-й слу-
		74	3
	3 или
	3 или
	3

чай (рис. 33а): обозначим искомое расстояние HG A1D x . Так как площадь тре-

23.05.2013. http://www.alexlarin.net/

угольника АВС равна 25, то его высота

AG 543 . Аналогично для треугольника

A B C

высота

AH 24

3 . Используя ра-

венство

AG AA1 A1H HG ,

составим

уравнение

2x 24

Отсюда

x 4

A1 x

Рис. 33а

2-й случай (рис. 33б). Обозначим искомое

расстояние

HG A1D y.

Используя равен-

ство

AG AA1 HG A1H , составим уравне-

ние 543 2y y 243. Отсюда y 743 . 3

C1 B1
H	D
	D

B G C

Рис. 33б

Произвольный четырехугольник

73. Продолжения сторон АD и ВС выпуклого четырехугольника ABCD пересекаются в точке М, а продолжения сторон АВ и CD – в точке О. Отрезок МО перпендикулярен биссектрисе угла АОD. Найдите отношение площадей треугольника АОD и четырехугольника ABCD,

если AO 12, DO 8, CD 2.

Ответ: 2:1 или 14:11. Указание. Из усло-

вия задачи следует, что ОМ является биссектрисой внешнего угла треугольника ADO (рис. 34а). Поэтому по свойству биссектрисы

Значит,

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

имеем

. Значит,

В треугольнике

ADO

проведем

отрезок

DH MB.

Из треугольника АВМ, используя

теорему Фалеса,

находим

Пусть AH x,

тогда BH 2x. Из треуголь-

ника HDO, используя теорему Фалеса, нахо-

дим

. Отсюда BO 6x.

Рис. 34а

Для треугольников ВОС и ADO с общим углом получаем

SBOC

BO OC

SAOD

AO DO

9x 8 2

SAOD 2 .

SABCD 1

A 8

B C M

Рис. 34б

Второй случай (рис. 34б) рассмотрите самостоятельно.

Параллелограмм

74. Высота CK параллелограмма ABCD равна 12. Найдите диагональ AC, если известно, что AD 13, CD 10, а точка K лежит на прямой AB.

Ответ: 369 или 13. Указание. См., «Решебник», Глава 2, задача 11.

75. В параллелограмме ABCD проведена биссектриса угла А, которая пересекает прямую ВС в точке K. Найдите пе-

23.05.2013. http://www.alexlarin.net/

риметр параллелограмма, если BK 5,

KC 2.

Ответ: 16 или 24. Указание. Показать,

что треугольник АВK – равнобедренный. Рассмотреть два случая.

1-й случай: пусть биссектриса пересекает отрезок ВС.

2-й случай: пусть биссектриса пересекает продолжение отрезка ВС за точку С.

76. Биссектрисы углов А и В параллелограмма ABCD делят сторону DС на три равных отрезка. Найдите стороны АВ и ВС параллелограмма, если его периметр равен 80.

Ответ: 16 и 24 или 10 и 30. Указание. См. «Пособие», пример 14.

77. (ЕГЭ, 2010). В параллелограмме ABCD биссектрисы углов при стороне AD делят сторону BC точками M и N так, что BM :MN 1:5. Найдите BC если AB 3.

Ответ: 3,5; 21. Указание. См. указания к предыдущему упражнению.

78. (МФТИ). Биссектрисы углов B и

Cпараллелограмма ABCD пересекаются

вточке O. Найдите площадь параллело-

грамма,	если	A 2arcsin	2	,

		13

OA 2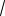10, OD 5.

Ответ: 24 или 72. Указание. Применить теорему косинусов для треугольников ABO и OCD.

79. На стороне BC параллелограмма АВСD выбрана точка E, делящая эту сторону в отношении 3:4. Отрезок DE пересекает диагональ AC в точке F. Какую часть площади параллелограмма АВСD составляет площадь треугольника AFD?

Ответ: 7 или 7 . Указание. См. «По-

20 22

собие», пример 10.

80.Дан параллелограмм ABCD. Точка

Млежит на диагонали BD и делит ее в отношении 2:3. Найдите площадь параллелограмма ABCD, если площадь четырехугольника ABCМ равна 60.

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

Ответ: 150 или 100. Указание. 1-й случай:

пусть		BM				2	(рис. 35а), тогда BM					2	BD

		MD			3						5
и S			2	S				1	S		(треугольники АВМ
	ABM				ABD					ABCD
		5					5

и ABD имеют общую высоту).

Рис. 35

Аналогично S

BCM

BCD

ABCD

Тогда S

ABCM

ABM

BCM

ABCD

Отсюда S

150 .

ABCD

ABCM

2-й случай, когда

(рис. 35б) рас-

смотрите самостоятельно.

81. В параллелограмме ABCD один из

углов равен 45 . Точки E и F являются серединами смежных сторон, образующих острый угол. Площадь треугольника, отсекаемого прямой EF от параллелограмма ABCD, равна S. Найдите площадь треугольника, вершинами которого служат точки E, F и C.

Ответ: S или 3S. Указание. См. «Посо-

бие», рисунок 47.

82. В треугольнике АВС через точку М, лежащую на стороне ВС, проведены прямые, параллельные сторонам АС и АВ. Площадь образовавшегося при этом па-

раллелограмма составляет	5	площади

	18

треугольника АВС. Найдите, в каком отношении точка М делит сторону ВС.

Ответ: 1:5 или 5:1. Решение. Пусть

BM	k , тогда	BM		k		и	CM		1
MC		BC		k 1			BC		k 1

(рис. 36). Обозначим площадь треугольника АВС через S. Тогда для подобных треугольников KВМ и АВС получаем равенство

		k	2
SBKM			S .

	k 1

23.05.2013. http://www.alexlarin.net/

Аналогично для подобных треугольников

LMC и

АВС

получаем

SLMC

S .

k 1

Площадь

параллелограмма

АKМL

равна

S .

или

(k 1)

2k 1

Согласно

условию

задачи

составим

уравнение

k2 2k 1

Отсюда

находим

или k 5.

5	Рис. 36

83. Точки P, R и Q лежат на сторонах соответственно EF, FG и EG треугольника EFG, причем EPRQ – параллелограмм,

площадь которого составляет 8 площа-

ди треугольника EFG. Найдите диагональ PQ параллелограмма, если известно, что

EF =15, EG =10 и FEG = 60°.

Ответ: 7 или 231 . Указание. См. «По-

собие», пример 28.

84. (ЕГЭ, 2011). Точки А, В и С лежат на сторонах соответственно KL, LM и KM треугольника KLM, причем KABC – параллелограмм, площадь которого со-

ставляет		площади треугольника KLM.

Найдите диагональ AC параллелограмма, если известно, что KL 8, KM 12 и

cos LKM 7 . 12

Ответ: 8 или 26 . Указание. См. преды-

дущую задачу.

85. В треугольник АВС со сторонами

AB 18 и BC 12 вписан параллелограмм BKLM, причем точки K, L, M лежат на сторонах АВ, АС и ВС соответственно. Известно, что площадь параллелограмма

составляет 4 площади треугольника

АВС. Найдите стороны параллелограмма.

Ответ: 6 и 8 или 4 и 12. Указание. См. «Пособие», пример 28. Аналогично приве-

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

денному там решению обозначить			LC	k и			Ромб
денному там решению обозначить				k и
			LA				Из вершины тупого угла ромба
	2		LA			87.	Из вершины тупого угла ромба
получить уравнение k2 k	2	0.			проведены две высоты. Расстояние меж-
получить уравнение k2 k		0.			проведены две высоты. Расстояние меж-

9ду их концами равно половине диагонали ромба. Найдите углы ромба.

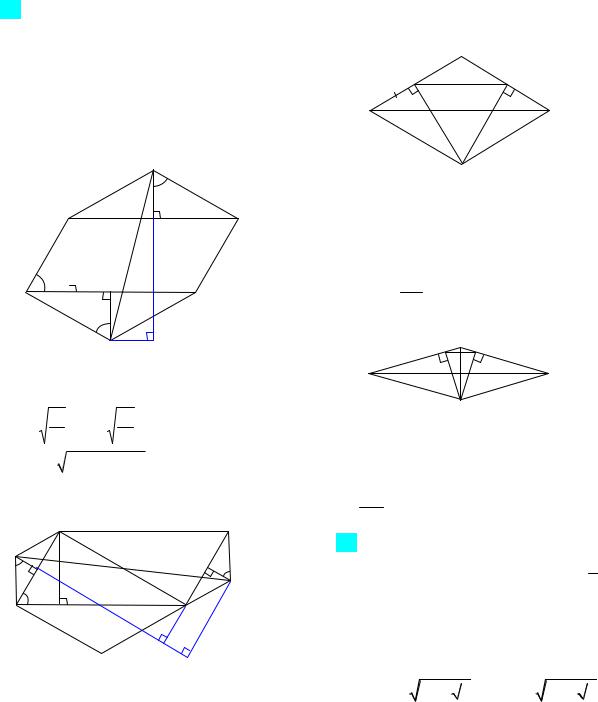
86.Дан параллелограмм со сторонами

1 и 2 и острым углом 60 . На двух его противоположных сторонах как на основаниях построены вне параллелограмма равнобедренные треугольники с углами 120 при вершинах. Найдите расстояние между этими вершинами.

				F
	B			60o
	B		2	C
1		h		H1
1		h
A	60o		H2	D
A	H		60o	D
			60o

E H3

Рис. 37а

Ответ: 13 или 19 . Указание. См. рис.

3 3

37а	(EF	EH32 FH3	2 , где	EH3 AH ,
FH3	EH2	BH FH1 ) и 37б.

	B		2		C
E	1		H	1	60
o			H		60
o			h		o
60	H2		h		F
A	60o		D
A	H	h	D
		h

Рис. 37б

23.05.2013. http://www.alexlarin.net/

M N

A C

Рис. 38а

Ответ: 60 ; 120 или 30 ; 150 .

Указание. Если 2MN AC (рис. 38а), то

MN средняя линия треугольника ABC .

Тогда AM AD .

M	B N
A	C
	D

Рис. 38б

Если 2MN BD (рис. 38б), то из подобия треугольников MND и ABD следует

MD AD .

88. Дан ромб со стороной, равной 1, и

острым углом при вершине, равным .

Точка K лежит на стороне ВС, причем BK KC . Найдите расстояние от вершины В до прямой АK.

Ответ:				1				или	1					.

	2			5 2						2 5 2
	2			5 2			3			2 5 2			3
Указание.	1-й		случай.				Пусть		A			(рис.
Указание.	1-й		случай.				Пусть		A			(рис.
		5							6
39а), B		5	. Отрезок BE						( BE AK ) –
39а), B			. Отрезок BE						( BE AK ) –
	6				1						1
искомый.	SABK				1	AB BK sin B					1	.	Из
искомый.	SABK					AB BK sin B						.	Из
				2					8

теоремы косинусов для треугольника ABK :

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

AK AB2 BK2 2AB BK cos B

5 2

, BE

SABK

5 2

Рис. 39

2-й случай. Пусть B

(рис. 39б). Тогда

5 2

SABK

2 5 23

89. В ромбе ABCD со стороной а и углом 60 проведены высоты CM и DK . Найдите длину отрезка MK .

	a		a 7
Ответ:		или a , или		. Указание.

2 2

См. «Решебник», Глава 2, задача 15.

90. Ромб вписан в прямоугольный треугольник с катетами 9 и 12 так, что одна из его вершин совпадает с вершиной острого угла треугольника, а три другие лежат на сторонах треугольника. Найдите площадь ромба.

Ответ: 135 или 80 . Указание. См. «Ре-

16 9

шебник», Глава 3, задача 1.

91. (ФИПИ, 2013). Две стороны треугольника равны 8 и 10, косинус угла

между ними равен 2 . В треугольник

Ответ: 5 или 10 . Указание. Показать, что

данный треугольник равнобедренный, и рассмотреть два случая, когда ромб и треугольник имеют общий угол (рис. 40а, б).

B B

D E L M

A F C A N C

а б

Рис. 40

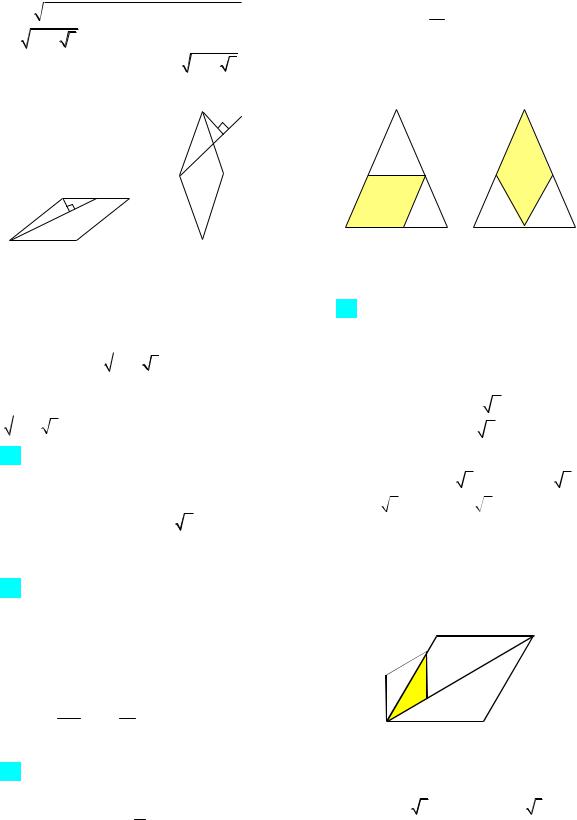
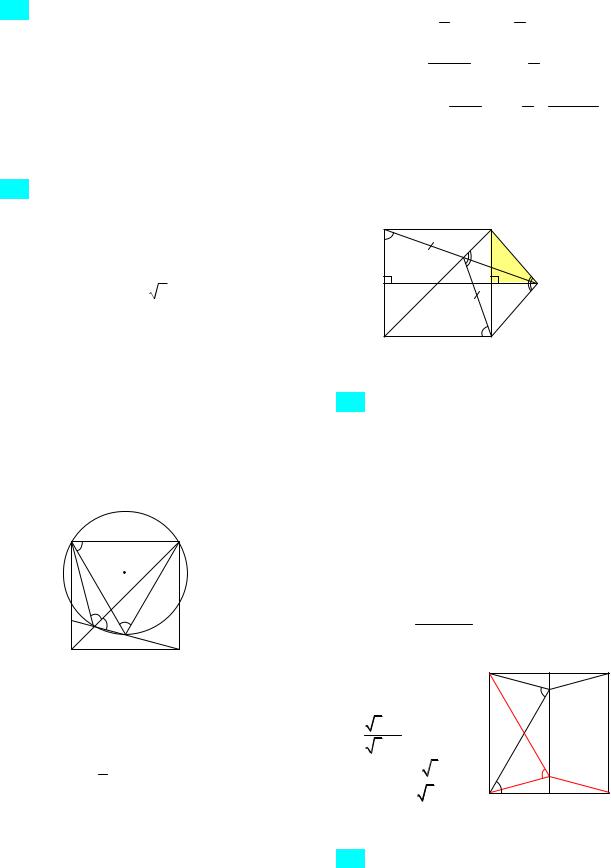
92. Два ромба ABCD и AMHK, имеющие общую вершину А, расположены так, что стороны АВ и АМ образуют угол в 30 . Известно, что углы при вершине А обоих ромбов равна 60 , площадь пере-

сечения ромбов равна 53 , а площадь их

объединения равна 23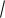3. Найдите площадь каждого из ромбов.

Ответ: SABCD 163, SAMHK 123 или

SABCD 123, SAMHK 163.

Решение. Исследование условия задачи показывает, что размещение ромбов зависит от положения точки Н на луче АВ. Обозначим стороны ромбов ABCD и AMHK через а и b соответственно.

B C

A D

Рис. 41а

1-й случай: пусть AH AB (рис. 41а). Так

как	SABCD	a2	3	и	SAMHK	b2	3	, причем
			2				2

вписан ромб, имеющий с треугольником общий угол (вершина ромба, противоположная вершина этого угла, лежит на третьей стороне треугольника). Найдите сторону ромба.

23.05.2013. http://www.alexlarin.net/

пересечение ромбов есть треугольник АНK, а объединение ромбов состоит из ромба ABCD и треугольника АМН, то получаем систему уравнений

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

a2		3 b2		3
a2		3 b2		3	23 3,

	2			4
	2			4

b2		3
b2		3	5	3.
	4		5	3.
	4

Отсюда имеем a 6, b 2 5 .
Из треугольника АНK, используя теорему
косинусов, находим	AH 2		. Что проти-
		15
воречит условию, так как AH AB .
2-й случай: пусть	AB AH 3AB (рис.

41б). Тогда пересечение ромбов есть четырехугольник АВЕK, объединение состоит из ромба ABCD и двух треугольников АМН и ВНЕ.

M B E C

A D

Рис. 41б

Из треугольника АМН по теореме косину-

сов находим AH b3 , а BH b3 a . Так как BEH 90 , EBH 60 , то

	SBHE		( 3b a)2 3								SAHK		b2	3
										,					,
						8				,				4	,
						8								4
				SABEK SAHK SBHE .
Составляем систему уравнений:
b2				a2			(		b a)2
		3			3			3				3
		3			3			3				3	23		3,


	4		2								8
	4		2								8

b2 3				( 3b a)2 3
b2 3				( 3b a)2 3							5 3.
	4					8					5 3.
	4					8

B K

A D

Рис. 41в

a 4 2

Получаем или

b 2 6

a 2 6

, что соответст-

b 4 2

вует рассматриваемому случаю AB AH (проверьте!). При этом площади ромбов принимают

одно из значений 123

или 163 .

23.05.2013. http://www.alexlarin.net/

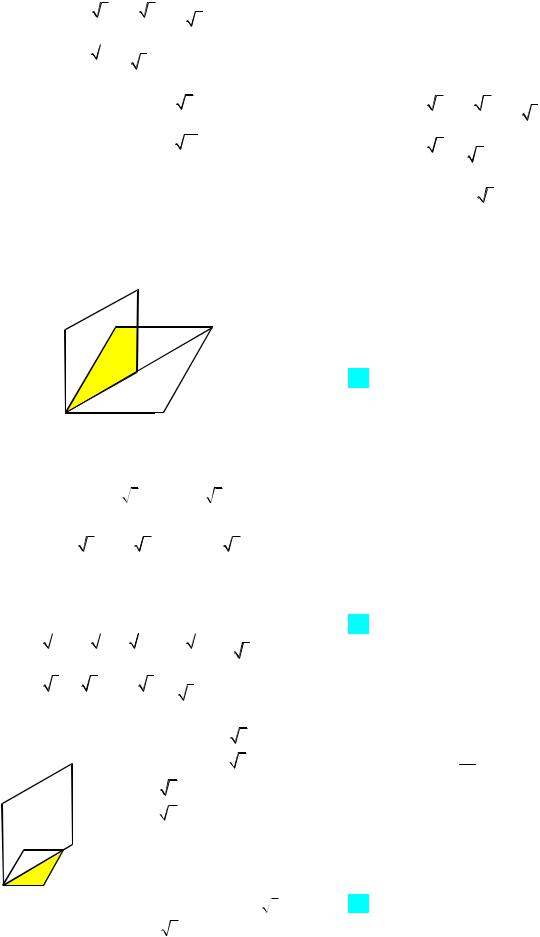
3-й случай: пусть AH 3AB (рис. 41в). В

этом случае пересечение ромбов есть треугольник АВС, а объединение состоит из ромба АМНK и треугольника АСD. Получаем систему уравнений

			b2		3 a2		3
			b2		3 a2		3		23 3,


			2		4

			a2		3
			a2		3	5	3.
						5	3.
			4
Отсюда			имеем			a 2
Отсюда			имеем			a 2		5, b 6 . Но тогда
AH 3AB.
				Прямоугольник
		В прямоугольнике ABCD AB 5,
BC	93.	В прямоугольнике ABCD AB 5,
BC		4.	Точка Е на прямой АВ выбрана

так, что AED DEC . Найдите АЕ.

Ответ: 2 или 8. Указание. См. «Пособие»,

пример 11.

94. В равнобедренный прямоугольный

треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Чему равны стороны прямоугольника, если известно, что они относятся как 5:2, а гипотенуза треугольника равна 45?

Ответ: 10; 25 или 7,5; 18,75.

Указание. Рассмотреть два случая:

1)на гипотенузе лежит большая сторона прямоугольника;

2)на гипотенузе лежит меньшая сторона прямоугольника.

95. В равносторонний треугольник АВС вписан прямоугольник PQRS так, что основание прямоугольника RS лежит на стороне ВС, а вершины P и Q – на сторонах АВ и АС соответственно. В каком отношении точка Q должна делить сторону АС, чтобы площадь прямоугольника

PQRS составляла 45 площади треуголь-

ника АВС?

Ответ:	AQ		5	или	AQ		9	. Указание.
	QC				QC
		9				5

Рассмотреть подобие треугольников PAQ и BAC.

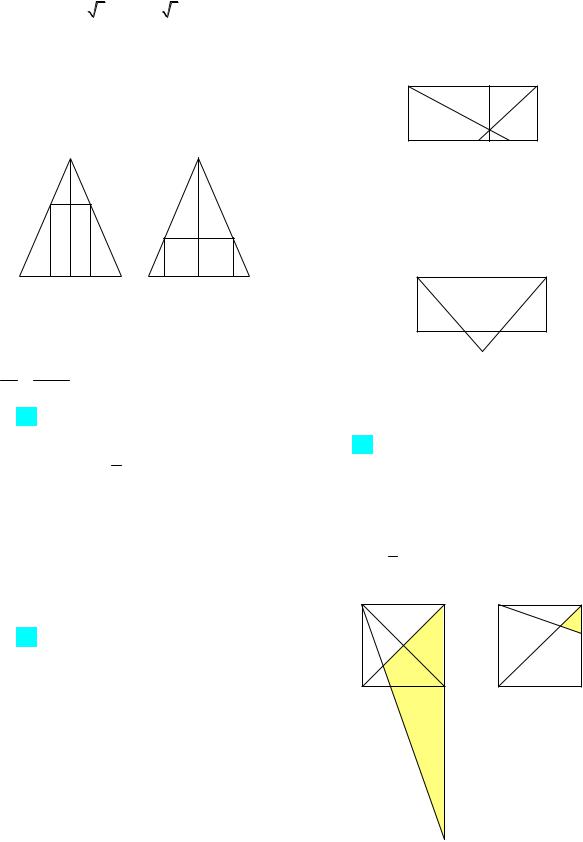
96. В треугольнике АВС AB BC 13,

AC 10. В треугольник вписан прямоугольник так, что две его вершины лежат

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

на стороне АС, а две другие – на сторонах АВ и ВС. Известно, что одна сторона прямоугольника вдвое больше другой. Найдите диагональ прямоугольника.

Ответ:

15 5

или

60 5

. Указание. Рас-

смотреть подобные треугольники BFE и ВСА

(рис. 42), и используя пропорцию

12 2x

AC BD

составить уравнение

10 12

B B

E K F

A G D H C A G D HC

а б

Рис. 42

Во втором случае составить уравнение

2x 12 x .

1012

97.Основание равнобедренного треугольника равно 56, косинус угла при

вершине равен 4 . Две вершины прямо-

угольника лежат на основании треугольника, а две другие – на боковых сторонах. Найдите площадь треугольника, если известно, что одна из его сторон вдвое больше другой.

Ответ: 882 или 1152. Указание. См. уп-

ражнение 96.

98. В прямоугольнике ABCD со сторонами AB = 4 и BC = 10 на стороне AD расположены точки M и N таким образом, что DM = 4, при этом P – точка пересечения прямых BN и CM. Площадь треугольника MNP равна 1. Найдите длину отрезка, соединяющего точки M и N.

Ответ: 2 или 2,5. Указание. 1-й случай:

пусть точка Р расположена внутри прямоугольника ABCD (рис. 43а). Пусть высота РЕ треугольника MNP равна x, а MN y . Рассмотрим подобие треугольников MNP и СВР,

23.05.2013. http://www.alexlarin.net/

и		составим отношение			PE	MN	или

	x		y		PF BC
				. Второе уравнение получаем, ис-

4 x 10

ходя из площади треугольника MNP: xy 2.

Решая систему уравнений, находим x 0,8 и y 2,5.

B	F	C
	P
A	M E N	D
	Рис. 43а

2-й случай (точка Р расположена вне прямоугольника ABCD) рассмотрите самостоятельно (рис. 43б).

B C

A N M D

Рис. 43б

Квадрат

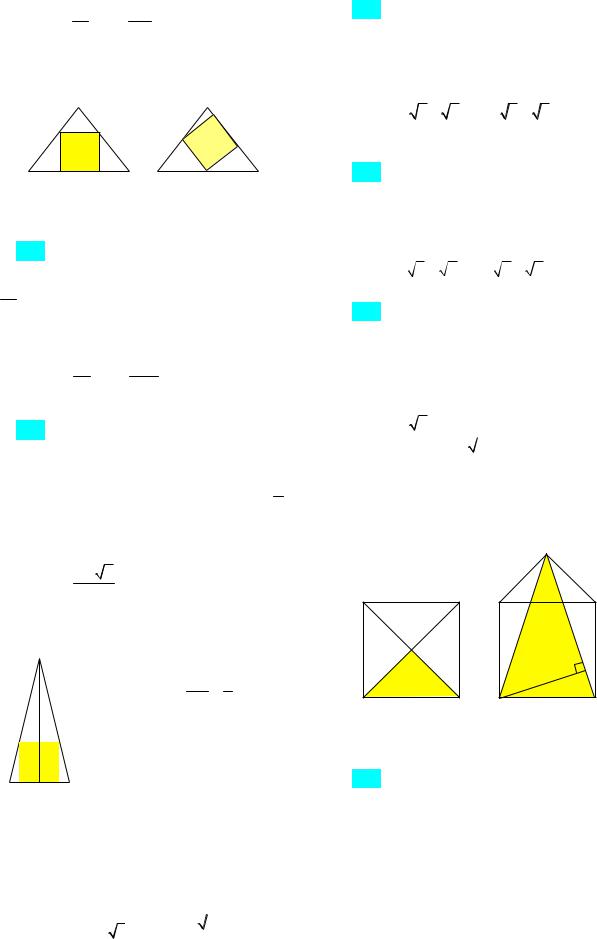
99. Точка K делит диагональ АС квадрата ABCD в отношении 1:3. Прямые ВK и СD пересекаются в точке Р. Найдите площадь треугольника KРС, если сторона квадрата равна 4.

Ответ: 2 или 18. Указание. См. рис. 44а, б.

B C B C

K P

A D A D

а б

Рис. 44

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

100. (МИОО, 2010). Прямая, прове-

денная через середину стороны AB квадрата ABCD, пересекает прямые CD и AD в точках M и T соответственно и образует с прямой AB угол, тангенс которого равен 4. Найдите площадь треугольника BMT, если сторона квадрата АВСD равна 8.

Ответ: 16 или 48. Указание. См. «Решеб-

ник», Глава 2, задача 3.

101. Через вершину С квадрата АВСD

проведена прямая, пересекающая диагональ ВD в точке K, а серединный перпендикуляр к стороне АВ – в точке М. Найдите DCK , если AKB AMB.

Ответ: 15 или arctg7 . Указание. 1-й

случай. Пусть точка М лежит между точками K и С (рис. 45). Точки А, В, K и М лежат на одной окружности. В силу симметрии квадрата относительно диагонали ВD имеемAKB BKC. Вписанные углы, опирающиеся на одну и туже дугу, BKM BAM . Так как AM BM , то треугольник АВМ равносторонний. Угол ВKС – внешний угол для треугольника DCK . Получаем

DCK BKC KDC 60 45 15 .

A	B
K	M
D	C
	Рис. 45

2-й случай. Пусть точка K лежит между точками М и С (рис. 46). Пусть AKB и сторона квадрата равна 2a. Тогда искомый

угол DCK . Для выполнения усло-

вия задачи необходимо выполнение условия

LBM

Так как

tg LBM

NM NL

, то составим уравнение

2a tg

23.05.2013. http://www.alexlarin.net/

Отсюда							или		после
Отсюда		tg		2 tg			или		после
			4			2
преобразований			tg 1 2 tg .					Исполь-
			tg 1				2
зуя формулы tg sin						и tg 1 cos ,
получим уравнение				cos		2		sin
получим уравнение
	4sin cos (cos sin ) 1 0,
которое заменой			t cos sin				сводится к
уравнению 2t2 t 1 0.
	C					B
	a			K
	a
	N					L	M
	a					L
	a		2a
	D		2a			A
	D					A
			Рис. 46
102. Дан квадрат ABCD. В плоскости
квадрата		взята	точка			M, такая, что
BM CM		и AMB 75 . Найдите вели-
чину угла ВМС.
Ответ:		60	или 150 . Указание. Пусть
сторона квадрата равна 2a (рис. 47). Так как
BM CM , то EF				серединный перпенди-
куляр	к	BC .	Пусть		MAF ,				тогда
MBE 75 ,			AMB 30 2 .					Из ра-
венства EM MF EF получаем уравнение
atg(75 ) atg 2a .						Отсюда		следует

tg2 2tg tg75 2					0.
			tg75
Учитывая, что					B	a	E		C
	tg75				B	a	E		C
	tg75					75o M
tg(30 45 )						75o M
	3 1			2a
		,
	3 1							M1
получаем tg			3			75o		M1
или	tg 2		3 .		A		F		D
или	tg 2		3 .			a	F		D
Отсюда		60				Рис. 47
или 15 .						Рис. 47
или 15 .
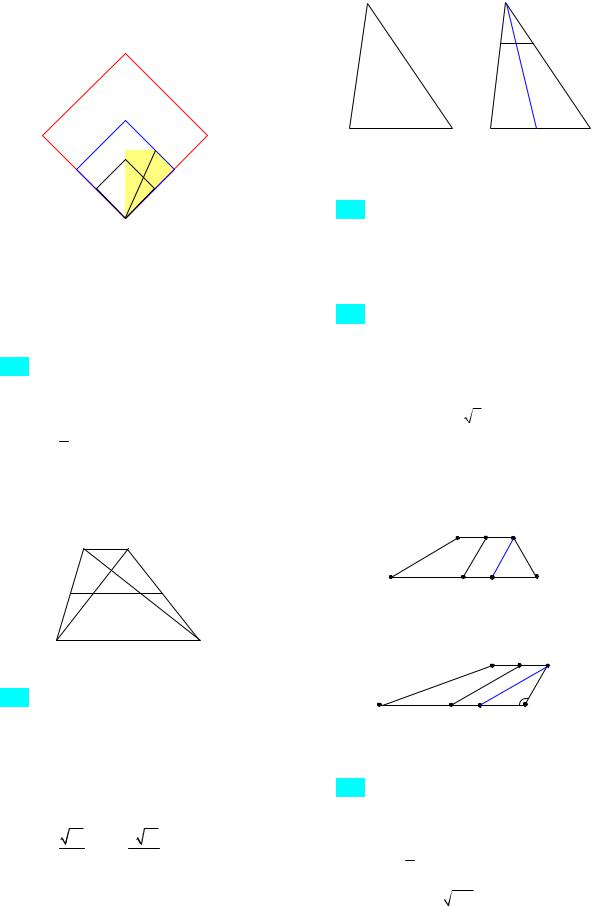
103. Все вершины квадрата лежат на
сторонах равнобедренного треугольника
АВС, основание АС которого равно 12, а
боковая сторона АВ равна 10. Найдите
сторону квадрата.
									48

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

Ответ: 24 или 240 . Указание. Рассмот-

5 49

реть подобие треугольников в двух случаях

(рис. 48а,б).

B BF

D E D G

A F G C A E C

а б

Рис. 48

104. Две стороны треугольника равны

10 и 13, косинус угла между ними равен

5 . Найдите сторону квадрата, все вер-

шины которого расположены на сторонах треугольника.

Ответ: 60 или 1560. Указание. См. уп-

11 189

ражнение 103.

105. В треугольник с основанием, рав-

ным а, вписан квадрат, одна из сторон которого лежит на основании треуголь-

ника. Площадь квадрата составляет 1 6

часть площади треугольника. Определите сторону квадрата.

Ответ: 3 6 а . Указание. Пусть MEDL

– \квадрат со стороной x, вписанный в данный треугольник ABC с высотой BK h, AC a (рис. 49). Из подо-

Bбия треугольников AEM и ABK имеем AE h . Из по-

добия треугольников EBD и

ABC имеем

. Отсю-

x K

да получаем

A M a

Рис. 49

т.е.

xa xh ah.

По усло-

вию ah 12x2 . Получаем систему уравнений

		2	,
ah 12x			,

a h 12x.

				3		а .
Отсюда h (5 2					6
	6)а , x				6
	6)а , x
			6
23.05.2013. http://www.alexlarin.net/

106. На стороне BC квадрата ABCD построен равносторонний треугольник BCP. Найти высоту треугольника APD, проведенную из вершины A, если известно, что сторона квадрата равна 2.

Ответ:	6	2	или	6	2	. См. зада-
				2
2

ча 2, «Решебник», Глава 3.

107. На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ABP, проведенную из вершины A, если известно, что сторона равна 4.

Ответ: 6 2 или 6 2 . См. задача 2, «Решебник», Глава 3.

108. На стороне CD квадрата ABCD построен равнобедренный прямоугольный треугольник CPD с гипотенузой CD. Найдите высоту треугольника АBР, проведенную из вершины А, если известно, что сторона квадрата равна 1.

Ответ:	2	или		3	. Указание. 1-й слу-

2			10

чай: точки Р и А лежат по одну сторону от прямой CD (рис. 50а).

2-й случай: точки Р и А лежат по разные стороны от прямой CD (рис. 50б).

			P
D	C	D	C
	P
			H

A	B A	B
а	Рис. 50	б
	Рис. 50

109. (МИЭТ, 2000). Два квадрата

ABCD и AMHK, расположены так, что стороны АВ и АМ образуют угол в 45 . Известно, что площадь пересечения квадратов равна 8,5, а площадь их объединения равна 34,5. Найдите площадь каждого из квадратов.

Ответ:	SABCD 25;	SAMHK 18	или
SABCD 18;	SAMHK 25.	Указание. Из	трех
			49

Корянов А.Г., Прокофьев А.А. Планиметрические задачи с неоднозначностью в условии(многовариантные задачи)

приведенных ситуаций на рис. 51 возможна только соответствующая положению квадрата AMHK. Далее вычислить площади треугольников AEF и AFM.

	H2
	H2
	H
K2	H1	B F C	M2
K2			M2

	K	M
	K1	M1
	A		D
	A		D

Рис. 51

Трапеция

Линейные и угловые элементы трапеции

110. Основания трапеции равны а и b. Найдите длину отрезка, высекаемого диагоналями на средней линии.

Ответ: 1 |a b|. Указание. Рассмотреть

два случая, когда a b или a b . Отрезки MP и QN – средние линии в треугольниках

ABC и BCD (рис. 52).

M M

B C A D

A D B K C

а б

Рис. 53

112. Вычислите периметр трапеции, боковые стороны которой 40 и 25, высота 24, а одно из оснований равно 10.

Ответ: 110 или 124. Указания. См. «По-

собие», рисунок 34.

113. Боковая сторона неравнобедренной трапеции равна 12 и образует с ее основанием угол 60 . Основания трапеции равны 16 и 40. Найдите длину отрезка, соединяющего середины оснований.

Ответ: 12 или 123 . Указание. Пусть точки E и F – середины оснований трапе-

ции (рис. 54а, б), CG||EF , CG EF . При-

менить теорему косинусов для угла D в треугольнике GCD.

B C

M N

P Q

A D

Рис. 52

111. Боковые стороны АВ и CD трапе-

ции ABCD равны 12 и 16 соответственно. Отрезок, соединяющий середины диагоналей, равен 6. Средняя линия трапеции равна 9. Прямые АВ и CD пересекаются в точке М. Найдите длину медианы МK в треугольнике ВМС.

Ответ: 41 или 5 41. Указание. Рас-

2 2

смотреть два случая, связанных с переобозначением вершин трапеции (рис. 53).

23.05.2013. http://www.alexlarin.net/

B E 8 C

60o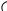

A	F 8 G 12 D

Рис. 54а

	B	E 8		C
		o	12
	120
A	F 8 G 12	D

Рис. 54б

114. Дана трапеция ABCD с боковыми

сторонами	AB 27,	CD 28 и основа-
нием	BC 5.	Известно,	что

cos BCD 2 . Найдите диагональ АС.

Ответ: 28 или 2181.

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.04.2019125.44 Кб48Razdel_4.doc
#
02.05.2015144.9 Кб38razlinovannyy_2003.doc
#
02.05.2015386.56 Кб34Referat.doc
#
01.12.201826.83 Кб7Referat_po_himii.docx
#
02.09.2019152.58 Кб12relef.doc
#
10.03.20161.61 Mб92Reshenie_S4_Dopolnenie_k_teorii.pdf
#
14.12.2019122.1 Кб3rup.docx
#
11.01.2020108.54 Кб2r_3.doc
#
02.05.2015538.28 Кб58sluchainye_sobytija.pdf
#
13.09.2019129.97 Кб6Soderzhanie_i_t_d.docx
#
15.09.20191.13 Mб22statistika(1).docx