нии молекулой фотонов различных, но близких энергий.

ε λмакс

λ (ν)

Результирующая спектральная полоса состоит из большого числа линий элек- тронно-колебательных переходов, которые, перекрываясь, образуют широкую полосу поглощения. Так как вероятность комбинированных переходов различна, полоса приобретает максимум и склоны различной крутизны.

Следственно, значение λмакс полосы в электронном спектре является мерой энергии электронного возбуждения молекулы. А величина εмакс служит мерой вероятности того, что при поглощении фотона данной энергии молекула перейдет в возбужденное состояние.

2. Анализ электронной структуры методами квантовой химии.

Квантово-химические методы исследования свойств органических молекул позволяют:

– получать информацию об электронной структуре молекулы, то есть распределении зарядов на атомах, характеристиках связей, а также

– вычислять энергию электронных уровней и устанавливать их конфигурацию, то

есть заполнение электронами.

Методы квантовой химии объясняют фотофизические и спектральные свойства

органических молекул, связывая эти свойства с особенностями строения, и поэтому широко используются для объяснения явлений цветности.

2.1. Способы описания энергетических состояний молекул.

Для качественного и количественного описания энергетического состояния молекул органическая химия использует два принципиально разных подхода. Это метод

валентных связей, который возник из теории резонанса, и метод молекулярных орби-

талей, имеющий квантово-механическое обоснование.

Метод валентных связей (ВС-метод) описывает строение органических молекул как суперпозицию (гибрид, смесь) всех возможных классических и поляризованных структур.

Каждая из этих структур отличается:

расположением простых и кратных связей,

расположением зарядов и неподеленных пар электронов,

различной внутренней энергией.

Например, строение фенола в основном и возбужденном состояниях можно описать, по меньшей мере, пятью π-резонансными структурами:

Однако основное и возбужденное состояние фенола может быть представлено различным вкладом (процентным содержанием) каждой их этих структур. Таким образом, описывается изменения в распределении электронной плотности, порядках связей и энергии молекулы при ее возбуждении светом.

Метод молекулярных орбиталей (МО-метод) представляет энергетические состояния молекулы как собственные значения энергии (Е) волновой функции (Ψ) многоэлектронной системы (молекулы, иона, радикала), интерпретируя электроны как волноподобные частицы. Такое предложение (постулат) в аналитической форме имеет вид уравнения Шрёдингера.

(пси) Н Ψ = Е Ψ , где Н - Гамильтониан или оператор энергии

Уравнение Шредингера в дифференциальной форме имеет точное решение только для одноэлектронных систем (молекулы водорода и гелия). Для нахождения функ-

ций многоэлектронных систем необходимо учитывать межэлектронные взаимодействия. Эта проблема решается в рамках теории самосогласованного поля (ССП) с по-

мощью итерационной процедуры. Для заданного набора одноэлектронных функций (орбиталей) орбиталей рассчитывается межэлектронное отталкивание, эта энергия затем используется для последующих расчетов новых наборов орбиталей и новых энергий отталкивания. Процесс продолжают до тех пор, пока не наступает сходимость и достигается самосогласование.

В связи с этим были предложены более совершенные операторы энергии, например, оператор Хартри-Фока (F). Его применяют в неэмпирических расчетах орбитальных энергий (ab initio) при решении системы уравнений Рутаана для различных органических молекул.

Широкому распространению квантовохимических методов способствовало применение приближенных методов расчета, которые отличаются большей простотой и наглядностью представления волновых функций. В этом случае делается ряд физически обоснованных предположений и упрощений.

Согласно теории МО многоэлектронная функция Ψ (пси) представляется как

произведение волновых функций ψ отдельных электронов, которые движутся (делокализованы) в поле всех атомных ядер и под влиянием потенциала отталкивания ос-

тальных электронов системы.

(пси-функция) Ψ = ψ 1 ψ 2 ψ 3 ... ψ n

Эти одноэлектронные пси-функции (ψi) получили название молекулярных орбиталей (МО). Энергетическое состояние молекулы в целом оценивается как сумма энергий её молекулярных орбиталей.

E (Ψ) = Σn E (ψn)

Далее делается допущение, что молекулярные орбитали ψi формируются как

линейная комбинация атомных орбиталей (АО) – одноэлектронных волновых функ-

ций атомов ϕn (фи). При этом волновая пси-функция выражается как сумма индивидуальных атомных орбиталей, умноженных на соответствующие весовые коэффициенты.

ψ i = c1ϕ1 + c 2ϕ 2 + c3ϕ3 + ... + cnϕ n

В методе ЛКАО отдельные атомы рассматриваются явно. Физическое обоснование этого приближения основано на том, что эффективная энергия электрона в момент его нахождения вблизи одного из атомных ядер молекулы в основном определяется потенциалом этого ядра.

Атомные орбитали ϕn , которые включены в молекулярную орбиталь ψi, называются базисными орбиталями. Минимальный базисный набор для молекул, содержащих атомы H, C, N, O, будет состоять из 1s, 2s, 2px,y,z орбиталей. Выражение ЛКАО (линейная комбинация атомных орбиталей) предполагает, что АО (ϕn) принадлежат различным атомам молекулы, причем каждый атом предоставляет для формирования МО только определенную АО.

Молекулярные орбитали (пси) ψi обладают всеми свойствами волновых функций. 1. Квадраты коэффициентов c2 при АО оценивают вероятность нахождения (пребывания) электрона на данной АО, то есть, представляет долю электронной плот-

ности на данной АО.

2. Численные значения коэффициентов при АО таковы, что сумма их квадратов равна 1 и соответствует заряду электрона. Тогда для любой МО можно записать

условие нормировки:

фи-Функция (ϕn) не имеет физического смысла, но её решение позволяет описать форму электронных облаков канонических АО. В отличие от собственной функции её квадрат представляет плотность вероятности нахождения электрона в определенной области пространства, то есть информирует о распределении электронной плотности в области ковалентного связывания.

Приближенный квантово-химический расчет для сложных молекул становятся возможными благодаря модификации способа решения уравнения Шредингера. В

рамках этого уравнения вариационный метод сводит квантовомеханическую задачу нахождения значений собственных энергий Ei и коэффициентов ciµ волновых функций ψi (МО) к математической задаче решения системы линейных однородных уравнений относительно значений коэффициента ciµ , имеющей вид:

Решению системы уравнений предшествует оценка значений

(Hµν) и (Sµν). Указанные интегралы рассчитывают на основе соответствующих атомных функций или заменяют параметрами.

Врасчетном методе МО Хюккеля используют три эмпирических параметра.

α–Кулоновский интеграл, который определяют из выражения:

αµ = ∫ϕµHϕµdτ (интеграл оператора энергии, µ=ν)

Кулоновский интеграл учитывает энергию электростатического взаимодействия

i-электрона с ядром µ, то есть является мерой электроотрицательности данного атома.

Заметим, что электроотрицательность элемента рассматривается, как способность атома удерживать свои электроны или мера его сродства к электрону. В пределах одного периода электроотрицательность возрастает с увеличением заряда ядра.

β – Резонансный интеграл, который определяется из выражения:

βµν = ∫ϕµHϕνdτ (интеграл оператора энергии, µ≠ν)

Резонансный интеграл учитывает энергию электрона, находящегося в поле соседних атомов µ и ν, которые образуют химическую связь, то есть служит мерой энергии связи между атомами. В методах МОХ β является условной (относительной) единицей энергии.

S – Интеграл перекрывания, который определяется из выражения:

Sµν = ∫ϕµϕνdτ

Интеграл перекрывания учитывает степень перекрывания (смешивания) АО атомов µ и ν, которые образуют химическую связь. Эффективность смешивания со-

относится с геометрическими условиями перекрывания АО, что, в конечном счете,

определяет энергию формирующейся молекулярной орбитали.

В простом методе МО Хюккеля Sµν принимается равным нулю, но в расширенном методе Хюккеля (РМХ), многих полуэмпирических методах, а также методе возмущения молекулярных орбиталей может принимать значения от 0 до 1.

Используяэтипараметры, преобразуюттакуюсистемууравненийвсистемувида:

Систему уравнений решают методом матричной алгебры и в итоге получают:

n значений собственной энергии молекулярных орбиталей Ei (по числу АО, формирующих МО) и

n наборов собственных коэффициентов сiµ, соответственно числу сформированных молекулярных орбиталей.

В методах МОХ энергия МО записывается в единицах β в виде выражения: E = α ± y β , где у - численный коэффициент

в других полуэмпирических методах в единицах энергии - эВ.

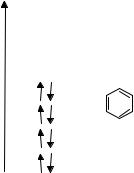
Например, решение квантово-механической задачи для бензола с учетом в базисе только шести pπ-орбиталей (π-приближение) дает 6 значений собственной энергии

Е1-Е6 и по 6 наборов коэффициентов ciµ для каждой из шести МО ψ1−ψ6 (см. рис).

Молекулярные орбитали заселяются также как и АО, в соответствии с правилом Паули, для них число заполнения N равно 0,1 и 2.

Шесть π-электронов бензола заселяют попарно три меньшие по энергии МО. Орбитали ψ1, ψ2, ψ3 оказываются занятыми МО. Согласно расчету ψ2 и ψ3 имеют одинаковую энергию, такие орбитали называются вырожденными. Среди занятых эти МО наибольшие по энергии и называются высшими занятыми МО (ВЗМО).

Симметрично занятым в бензоле сформированы три свободные или вакантные молекулярные π-орбитали ψ4, ψ5 и ψ6. Две из них также являются вырожденными МО. Среди вакантных МО орбитали ψ4, ψ5 меньше по энергии и поэтому называют-

ся низшими вакантными МО (НВМО).

Наиболее близкие по энергии ВЗМО и НВМО принято называть граничными ор-

биталями.

Собственные коэффициенты ciµ МО являются основой для оценки некоторых физических и химических свойств молекулы. Так как коэффициенты находят из условия нормировки, каждое значение ciµ позволяет оценить вклад каждой АО в формируемую i-МО. Если ciµ равно 1, то данная МО полностью локализована на µ-й АО.

Такая МО называется несвязывающей молекулярной орбиталью и обозначается как

n-МО. В молекулах, которые содержат гетероатомы (азот, кислород, сера и др.), неподеленные пары электронов гетероатомов могут занимать несвязывающие МО.

Значения собственных коэффициентов МО позволяют вычислить основные па-

между атомами образуется в результате перекрывания и смешивания базисных орби-

талей различных типов (АО, МО, гибридных, фрагментных). В итоге формируется связывающая МО, на которой располагается пара электронов с антипараллельными спинами. Если нет перекрывания однократно занятых орбиталей, нет связи.

Ковалентная связь возникает в направлении максимального перекрывания базисных орбиталей. Реализация этого принципа в значительной мере определяет:

геометрию образующейся молекулы;

энергетическую стабилизацию молекулярной системы, поскольку на энергетической оси связывающая МО располагается ниже базисных орбиталей.

Поэтому результат взаимодействия орбиталей зависит от формы, размера электронных облаков и их взаимной ориентации в пространстве.

Возможны два типа перекрывания, в которых принимают участие орбитали, имеющие р-характер (p-, sp-, sp2-, sp3-орбитали).

σ -перекрывание или фронтальное перекрывание происходит, когда оси симмет-

рии орбиталей лежат на одной прямой. Этому условию отвечает и перекрывание со сферическими s-орбиталями, например, при возникновении C-H связей. Такой тип взаимодействия мало зависит от взаиморасположения других осей координат взаимодействующих атомов или молекулярных фрагментов. В данном случае интеграл перекрыва-

ния Sσ всегда больше нуля. Его значение меняется от 0,85 до 0,6 и зависит от гибридного состояния атома и отчасти, к какому периоду принадлежит атом.

π -перекрывание или боковое перекрывание возможно, когда оси взаимодейст-

вующих орбиталей параллельны. Наилучшим образом этому условию могут удовлетворять рz-АО и π−МО, тогда величина интеграла перекрывания Sπ больше нуля.

Очень важно, что Sπ может меняться в диапазоне 0,2 – 0,0, что сильно зависит от геометрического фактора. Эффективнее всего перекрываются электронные облака атомов одного периода. Нарушение параллельности осей симметрии электронных облаков также снижает величину интеграла перекрывания и при

относительно линии связи перекрывание по π-типу становится невозможным. Вместе с тем, даже при наиболее благоприятных условиях перекрывания

значение интегралов перекрывания Sπ , всегда меньше чем Sσ .( Sπ < Sσ ).

Согласно теории возмущения молекулярных орбиталей Дьюара, формирование

новых МО рассматривается как возмущение взаимодействующих атомных или моле-

кулярных орбиталей. (М. Дьюар, Р. Догерти. Теория возмущений молекулярных орбиталей в органической химии, Мир, 1977 г).

На диаграмме орбитальных энергий процесс формирования МО изображается следующим образом:

σ

Возмущение выглядит так, как будто взаимодействующие орбитали µ и ν отталкиваются, сдвигаясь в противоположные стороны относительно своего первоначального положения на величину R , которую называют расщеплением.

Расщепление между вырожденными орбиталями, то есть орбиталями с одинако-

вой энергией, называют возмущением первого порядка. Например, такая ситуация возникает при образовании этана в результате взаимодействия двух метильных радикалов при перекрывании их sp3-орбиталей, несущих по неспаренному электрону.

Возмущение первого порядка всегда приводит к максимальному расщеплению.

В этом случае расщепление R равно резонансному интегралу, а величину расщепления вычисляют по уравнению:

Расщепление между орбиталями различной энергии (это наиболее частый слу-

чай) называют возмущением второго порядка. При этом энергетически более низкая орбиталь смешивается связывающе с более высокой и уменьшает энергию (стабилизируется). Напротив, энергетически более высокая орбиталь смешивается разрыхляю- ще и увеличивает энергию (дестабилизируется).

Например, такая ситуация возникает при образовании молекулы этиламина в результате взаимодействия двух радикальных частиц, в которых углерод находится в состоянии sp3-гибридизации, а азот в состоянии sp3- или sp2- гибридизации.

Возмущение второго порядка приводит к меньшему расщеплению R, поскольку величина расщепления обратно пропорциональна разности энергии взаимодействующих орбиталей ∆Еµν. В случае возмущения второго порядка величину расщепления R вычисляют по уравнению:

В результате из однократно занятых орбиталей образуется новая пара молекулярных орбиталей. Меньшая по энергии заполняется парой электронов, осуществляющих ковалентную связь, и становится связывающей. Парная ей с большей энергией остается незаселенной, вакантной и становится разрыхляющей.

Энергетическая щель - разность между связывающей и разрыхляющей орбиталями свидетельствует о выигрыше энергии при образовании данной связи.

Перекрывание и смешивание дважды занятых орбиталей также возможно и при-

водит к стабилизации системы, если хотя бы одной орбитали соответствует парная разрыхляющая орбиталь той же симметрии, то есть она является молекулярной или фрагментной.

Примером может служить формирование системы π-МО в этиленамине. Представим, что рекомбинация двух радикальных частиц, полученных из этилена и аминогруппы, совершается в два этапа. Сначала происходит фронтальное перекрывание и смешивание однократно занятых sp2 и px орбиталей частиц, которое завершается образованием σ-связи (предыдущий пример). Затем в молекуле совершается вынужденное смешивание π- и π*- МО этилена и pz-АО азота, несущей неподеленную пару электронов, которое завершается формирование трех МО π–типа.

π2

πµ

πν (pz-N атома)

π1

В этом случай из-за значительной разницы в энергии между одной из перекрывающихся орбиталей π*µ и πν взаимодействие будет сопровождаться возмущением второго порядка и меньшим расщеплением, чем расщепление между πµ и πν . Поэтому произойдет уменьшение размера энергетической щели между новыми разрыхляющей и высшей занятой МО.

Следует отметить, что взаимодействие между несколькими (три и больше) орбиталями аддитивно и итоговое возмущение не зависит, в какой последовательности рассматривались эти взаимодействия.