1.3.1. Конфигурация электронно-колебательных уровней

Образование ковалентной связи между двумя атомами XиY сопровождается:

• повышением электронной плотности в области между ядрами;

• сближением атомов с их фиксацией на определенном расстоянии r₀, которое соответствует длине этой связи;

• понижением энергии молекулярной системы на величину, равную энергии образовавшейся связи.

Таким образом, электронная энергия связи для двухатомной молекулы является функцией межъядерного расстояния,Е_пот=f(r_x-y).

Графически такую зависимость можно представить в виде характеристической кривой, имеющей форму искаженного параболоида, с энергетическим минимумом над точкой равновесного межъядерного расстояния r₀. Эта энергетическая кривая соответствуетсвязывающей молекулярной орбитали.

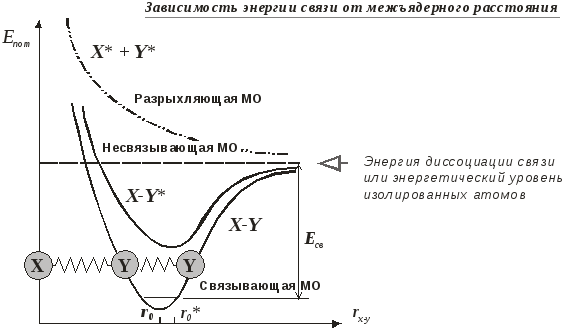
Минимум на кривой возникает потому, что при дальнейшем сближении атомов начинают преобладать силы межъядерного отталкивания. Расхождение атомов на большее расстояние также требует дополнительной энергии для преодоления сил ковалентного связывания. По мере увеличениямежъядерногорасстоянияправая ветвь кривой приближается к энергетическому уровню изолированных атомов и, наконец, наступаетдиссоциация молекулы. Таким образом, разность между уровнем энергии диссоциированных атомов и нулевым уровнем молекулы соответствует энергии данной связиЕ_свили равна энергии диссоциацииЕ_дис, взятой с обратным знаком.

Если сближение атомов не сопровождается возникновением связи между ними, характер энергетической кривой существенно изменяется. По мере уменьшения межъ­­ядерного расстояния r_x-yсилы отталкивания ,быстро нарастают, и энергетическая кривая приобретает виды экспоненты, что соответствуетразрыхляющей молекулярной орбитали.

В возбужденном состоянииэлектрон заселяет более высоко расположенный вакантный электронный уровеньи осуществляетодноэлектронную связьв молекуле. Энергия такой связи значительно меньше обычной двухэлектронной связи, поэтому длина связиr₀несколько увеличивается. При этом соответствующая кривая зависимости энергии от межъядерного расстояния, хотя и сохраняет форму параболоида, потенциальная яма становится менее глубокой и её правый склон более пологим. Понятно, что для высших возбужденных электронных состояний эта тенденция еще больше усиливается и, в конце концов, межатомная связь практически исчезает, а параболическая кривая превращается в экспоненту.

Для многоатомной молекулызависимостьЕ_потот межъядерных расстояний пре­вращается вмногомерную гиперповерхность, которая имеет энергетические миниму­мы, соответствующие равновесным конфигурациям атомов. Гиперповерхность опи­сывается в многопараметровой системе координат. Такая модель сложна и не облада­ет наглядностью.Поэтому приближенно используют сечение потенциальной гиперпо­верхности по координате наиболее слабой в данной молекуле связи.Эта координата сильнее других изменяется в ходе фотофизических процессов. Таким образом, мно­гомерный случай сводят к двухмерному, который рассмотрим более подробно.

Спектр поглощения органических соединений состоит из широких полос, а не из узких линий. Это объясняется тем, что любая молекула при фотовозбуждении изменяет не только электронную, но и колебательную энергию.

Колебаниясвязанных ядер вдоль межъядерной оси можно рассматривать как колебания ядраYотносительно неподвижного ядраX. При небольших отклонениях ядраY от положения равновесияr_oмолекулу приближенно рассматривают какгармонический осциллятор, а зависимость величины потенциальной энергииЕ_потот отклонения ядер изображается искаженным параболоидом (т.н.кривая Морзе). Общая колебательная энергия ядер ­­-­­­ сложная величинаЕ_кол=Е_пот +Е_кин

Из-за относительно малой массы ядер, их колебания квантуются.

Для данного электронного состояния колебательная энергия принимает лишь определенные величины в соответствии со значениями колебательных квантовых чисел v= 0,1,2,3… и может быть вычислена по уравнению Морзе.

Из этого уравнения следует, что низшая колебательная энергия ­­- энергия нулевого колебательного уровня отлична от нуля, так как Е_кол(0)h.

Теперь рассмотрим некоторые свойства потенциальной кривой электронного состояния колебательной системы.

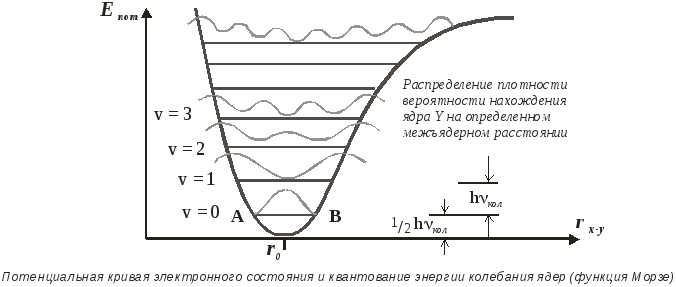
Точки пересечения разрешенных колебательных уровней полной энергии с потенциальной кривой (например, точки А и В) можно сопоставить с точками максимальной амплитуды колебаний гармонического осциллятора. В этих точках вся кинетическая энергия осциллятора превращается в потенциальную энергию. В промежуточных точках горизонтальных отрезков кинетическая энергия колеблющихся атомов отличается от нуля. Согласно уравнению при возрастании колебательного квантового числа колебательные уровни сближаются.

В виде синусоидальных кривыхна рисунке показанораспределение плотности вероятности нахождения ядра Yна определенном межъядерном расстоянии. При повышении колебательной энергии возрастает вероятность нахождения ядра вблизи потенциальной кривой. Напротив, на нулевом колебательном уровне максимум вероятности нахождения ядраYсовпадает с равновесным межъядерным расстояниемr₀.

Форма потенциальной кривой особенно сильно отличается от симметричной параболыв области малых межъядерных расстояний. Вследствие эффекта отталкивания ядер она круто идет вверх. В области больших межъядерных расстояний из-за ослабления ковалентной связи кривая идет более полого. Поэтому энергетику потенциальной кривой описываютфункцией Морзе, которая при определении колебательной энергии учитывает энергию диссоциации связи.