
Лекции прикладная оптика / Lec2_2015
.pdf
Лекция 2
ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
1. Основные понятия и определения
Значительная часть вопросов прикладной оптики вполне удовлетворительно может быть разрешена с помощью положений геометрической оптики, хотя в некоторых случаях правильное решение возможно лишь с позиций квантовой и волновой теории света. Геометрическую оптику можно рассматривать как предельный случай физической оптики, когда 0. Положения геометрической оптики имеют чисто геометрический характер.
Светящаяся точка - источник излучения, не имеющий размеров.
Световой луч - это линия, вдоль которой распространяется энергия излучения. Световому лучу в физической оптике соответствует нормаль к поверхности световой волны.
Оптическая длина луча - сумма произведений расстояний, последовательно проходимых лучом в различных средах, на показатели преломления соответствующих сред.
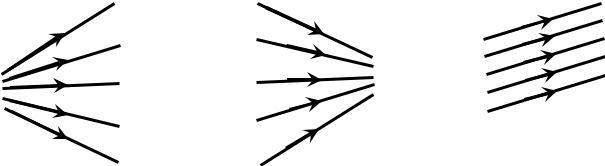
Если поверхность волны - сфера, то все нормали к ней, а следовательно, и все лучи сходятся в одной точке, а именно в центре сферы. Совокупность таких лучей называется гомоцентрическим пучком, т. е. пучком, имеющим общий центр.
1. Основные понятия и определения геометрической оптики
Пучок, лучи которого расходятся из общего центра, называется расходящимся гомоцентрическим пучком (рис. 1, а), если же лучи идут по направлению к центру пучка, то пучок называется сходящимся гомоцентрическим (рис. 1, б). Если гомоцентрический пучок распространяется от светящейся точки, находящейся в бесконечности, то он будет параллельным
(рис. 1, в).
Рис. 1 Гомоцентрические пучки лучей
а) |
б) |
в) |
Центр гомоцентрического пучка, входящего в оптическую систему, называется предметной точкой, а центр гомоцентрического пучка, вышедшего из оптической системы, называется
изображением предметной точки.
1. Основные понятия и определения геометрической оптики
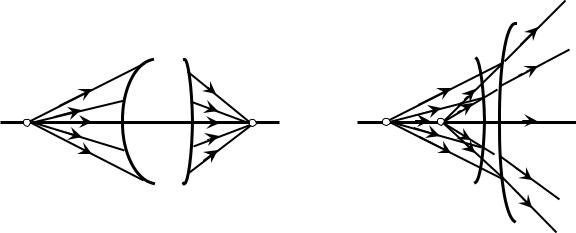
Всякий предмет и его изображение в геометрической оптике рассматриваются как совокупность предметных точек и их изображений. Поэтому для того, чтобы найти изображение того или иного предмета, нужно найти изображения его отдельных точек. Если после прохождения через оптическую систему пучки лучей сохраняют гомоцентричность, то каждой точке предмета соответствует только одна точка изображения. Две точки, одна из которых является изображением другой, называют сопряженными (рис. 2).
А’
А |
А’ |
А |
Рис. 2 Предметная точка А
иее изображение
а– действительное;
б - мнимое
а) |
б) |
В геометрической оптике изображение точки принято отмечать той же буквой, что и предмет, но со штрихом. Это относится и к другим обозначениям. Изображение, образованное пересечением самих лучей, называют действительным, а изображение, образованное пересечением их геометрических продолжений, - мнимым. Действительное изображение может быть спроецировано на экран, например, на фотопластинку. Мнимое изображение спроецировать на экран нельзя, но оно может быть рассмотрено глазом так же, как и действительное изображение.
1. Основные понятия и определения геометрической оптики
Все пространство, в котором распространяются пучки лучей, можно разделить на две части:
Пространство предметов - пространство, в котором находятся точки предметов.
Пространство изображений - пространство, в котором расположены изображения точек пространства предметов.
Оптической системой в геометрической оптике называют совокупность оптических деталей (призм, линз, зеркал и т.п.), предназначенную для формирования пучков световых лучей.
Любая оптическая деталь ограничивается поверхностью.
Поверхности могут быть плоскими, сферическими, асферическими и др.
Оптическую систему называют центрированной, если центры сферических поверхностей или оси симметрии других поверхностей лежат на одной прямой, которую называют оптической осью.
Любая плоскость, содержащая оптическую ось, называется меридиональной.
1.Основные понятия и определения геометрической оптики
Вгеометрической оптике для оценки отрезков и углов используют правила знаков (ГОСТ 7427-76. Геометрическая оптика. Термины, определения и буквенные обозначения.).
За положительное направление света принимают направление распространения его слева направо. Для каждого отрезка указывается направление отсчета.
Для определения знаков углов выбирают оси, от которых отсчитывают углы.
Отрезки вдоль оптической оси считаются положительными, если их направление совпадает с положительным направлением света, а отрицательными - при обратном направлении.
Отрезки, перпендикулярные к оптической оси, считают положительными, если они расположены над оптической осью, и отрицательными, если они расположены под осью.
Радиусы кривизны, отрезки, характеризующие положение предметов и изображений, отсчитывают от вершин соответствующих поверхностей.
Угол считается положительным, если для описания части плоскости между его сторонами ось, от которой ведется отсчет, нужно вращать вокруг вершины угла по часовой стрелке, и отрицательным - в противном случае.
2. Законы геометрической оптики
Теория геометрической оптики основана на использовании четырех физических законов:
Закон прямолинейного распространения света Закон независимости распространения световых пучков Закон отражения света Закон преломления света
2. Законы геометрической оптики
Закон прямолинейного распространения света.
Согласно этому закону свет между двумя точками в однородной и изотропной среде (в среде, оптические свойства которой не зависят от положения точки и от направления луча) распространяется по прямой, соединяющей указанные точки. На основе закона прямолинейного распространения света обычно объясняют возникновение теней и полутеней, явления солнечных и лунных затмений. Все самые точные физические и астрономические измерения основаны на применении этого закона.
Наглядно закон прямолинейного распространения света можно проиллюстрировать, если непрозрачный предмет осветить источником, размеры которого малы по сравнению с расстоянием до предмета. В этом случае наблюдается подобие между контуром предмета и его тенью на экране, которое соответствует геометрическому проецированию с помощью прямых линий.
Закон прямолинейного распространения света неприменим в тех случаях, когда пучок лучей проходит через диафрагму с очень малым отверстием, край любой диафрагмы или когда на пути пучка помещена малая непрозрачная преграда. В этих случаях свет распространяется далеко за край тени или полутени вследствие явления дифракции. Угол отклонения , вызванный
дифракцией, зависит от многих факторов и для круглого отверстия определяется формулой sin / D , где - длина волны, a D - диаметр диафрагмы. Подавляющее большинство
оптических систем имеет большие поперечные размеры по сравнению с длиной волн, поэтому при разработке теории этих систем явление дифракции можно не учитывать. При = 546 нм и D = 80 мм угол отклонения составляет всего ~ 2".
2. Законы геометрической оптики
Закон независимости распространения световых пучков. Сущность закона заключается в том, что отдельные лучи и пучки, встречаясь и пересекаясь друг с другом, не оказывают взаимного влияния.
В геометрической оптике считают, что если несколько пучков падают на одну и ту же площадку или сходятся в одной точке, то действия этих пучков складываются. Интерференцией при этом пренебрегают.
Явления интерференции и дифракции необходимо учитывать при анализе процесса образования изображения, так как это позволяет объяснить распределение световой энергии в кружке рассеяния и судить о качестве изображения.
2. Законы геометрической оптики
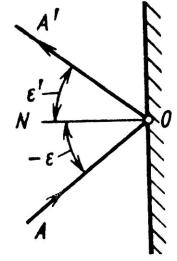
Закон отражения света. Если лучи, распространяясь в однородной оптической среде, встречают зеркальные или полированные поверхности, то они полностью или частично отражаются в соответствии с законом отражения, который формулируется следующим образом:
1.Луч падающий АО, нормаль к отражающей поверхности в точке падения NО и луч отраженный ОА' лежат в одной плоскости (рис. 3).
2.Угол отражения ' по абсолютной величине равен углу падения, .
3.Луч падающий и луч отраженный обратимы. Следовательно, если падающий луч направить по пути А'О, то он отразится в направлении ОА. Принцип действия зеркал и отражательных призм, используемых в качестве деталей оптических приборов, основан на законе отражения света.
Рис. 3 Отражение света от зеркальной поверхности
