
Лекции прикладная оптика / Lec3_2015
.pdf
Лекция 3
ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
Понятие об идеальной оптической системе. Кардинальные элементы
Идеальная оптическая система - такая система, которая любую точку пространства предметов изображает стигматически, т.е. она не нарушает гомоцентричности прошедших через нее широких пучков лучей в пределах большой области пространства.
Теория идеальной оптической системы имеет чисто геометрический характер.
Она является частным случаем более общей геометрической задачи о преобразовании одного пространства в другое, которое называют коллинеарным преобразованием. Каждому множеству точек одного пространства соответствует множество точек в другом пространстве, которое можно назвать изображением первого.
Воснове коллинеарного соответствия лежат следующие соображения:
каждой точке пространства предметов соответствует только одна точка в пространстве изображений; эти две точки являются сопряженными;
всякой прямой линии пространства предметов соответствует только одна сопряженная с ней прямая линия в пространстве изображений
всякой плоскости пространства предметов соответствует только одна сопряженная с ней плоскость в пространстве изображений.
Всопряженных плоскостях, которые перпендикулярны оптической оси, сохраняется строгое подобие.
Понятие об идеальной оптической системе. Кардинальные элементы
Определение понятий кардинальных (основных) элементов идеальной оптической системы.
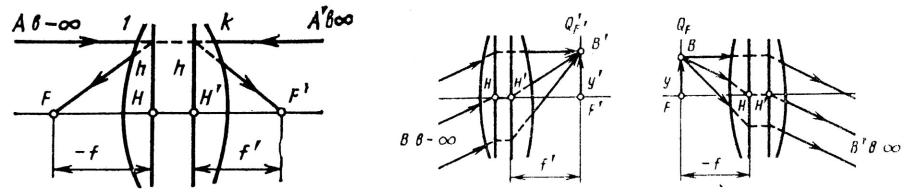
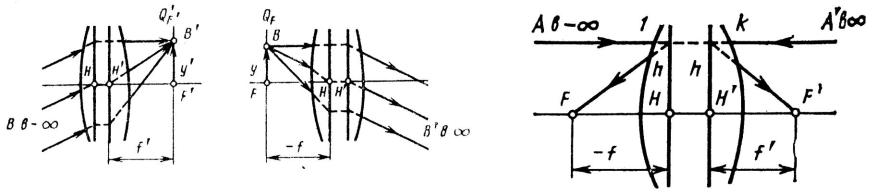
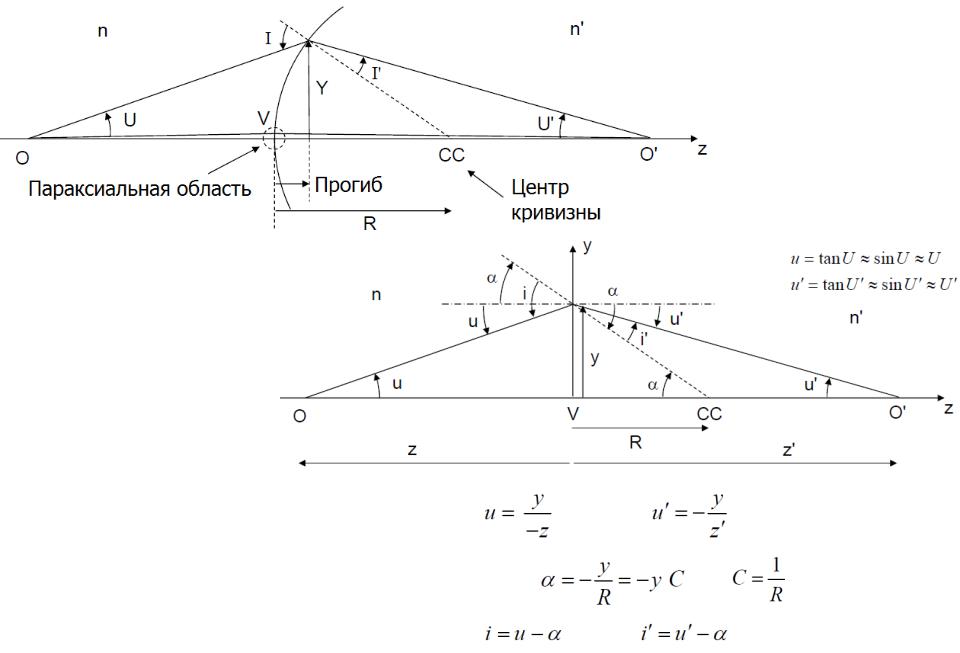
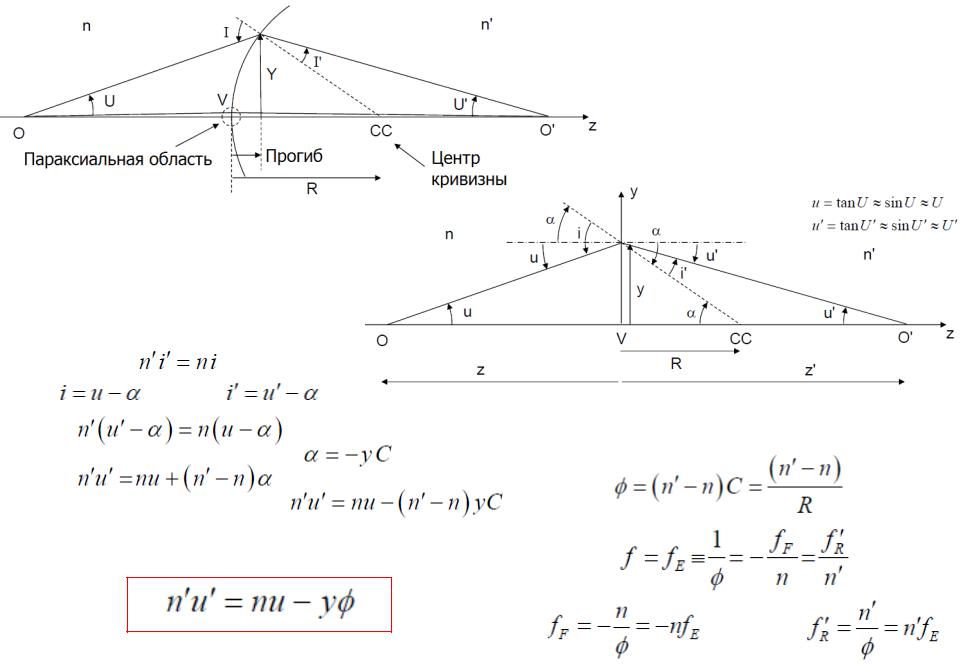
Представим оптическую систему, состоящую из ряда поверхностей, в которой 1 и k являются первой и последней поверхностями, и рассмотрим три характерных положения предметной точки и ее изображения.
1.Светящаяся точка А находится на оптической оси в бесконечности. Ее изображение будет в точке F', которую называют задним фокусом оптической системы. Плоскость, проходящая через задний фокус и перпендикулярная оптической оси, называется задней фокальной плоскостью оптической системы. Эта плоскость является изображением бесконечно удаленной плоскости. Пучок лучей, выходящий из бесконечно удаленной точки на оптической оси, приходит в оптическую систему в виде пучка, параллельного оптической оси. Следовательно, задний фокус обладает тем свойством, что через него проходит всякий луч, входящий в оптическую систему параллельно оптической оси. Если предметная точка В (рис. 14, а), удаленная в бесконечность, находится вне оптической оси, то лучи, выходящие из этой точки, образуют наклонный пучок параллельных лучей. Этот пучок по выходе из оптической системы собирается в сопряженной точке В', которая находится вне оптической оси, в задней фокальной плоскости Q'F ' .
Понятие об идеальной оптической системе. Кардинальные элементы
1.При перемещении предметной точки А вправо точка А' будет перемещаться также вправо и удалится в бесконечность. В этом случае точка А переместится в точку F. Точку F на оптической оси в пространстве предметов, сопряженную с бесконечно удаленной точкой оптической оси в
пространстве изображений, называют передним фокусом оптической системы. Плоскость QF, перпендикулярную оптической оси и проходящую через передний фокус, называют передней фокальной плоскостью. Передняя фокальная плоскость сопряжена с бесконечно удаленной плоскостью пространства изображений. Следовательно, пучок лучей, выходящий из любой точки В
передней фокальной плоскости QF (кроме переднего фокуса), выходит из системы наклонным пучком параллельных лучей. Всякий луч, входящий в оптическую систему через передний фокус, выходит из системы параллельно ее оптической оси.
Понятие об идеальной оптической системе. Кардинальные элементы
1.Выберем пару сопряженных и перпендикулярных оптической оси плоскостей, в которых линейное увеличение равно плюс единице. Эти плоскости называют передней и задней главными плоскостями. Точки их пересечения с оптической осью называют передней H и задней H' главными точками. Так как линейное увеличение в главных плоскостях равно +1, то всякий отрезок в одной плоскости изображается равным и одинаково расположенным отрезком в другой плоскости. Отсюда следует, что входящий и выходящий лучи пересекают соответствующие главные плоскости на равных высотах h.
Кардинальные точки оптической системы
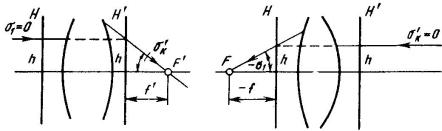
Понятие об идеальной оптической системе. Кардинальные элементы
Расстояние HF от передней главной точки Н до переднего фокуса F является передним фокусным расстоянием оптической системы, а расстояние H'F' от задней главной точки H' до заднего фокуса F'- задним фокусным расстоянием. Фокусные расстояния обозначают соответственно f и f'. Их отсчитывают от главных точек.
Если оптическая система находится в однородной среде, например в воздухе (п = п' = 1), то f' = -f, т. е. заднее и переднее фокусные расстояния равны по абсолютному значению. В общем случае при п' п f / f ' n / n'.
Так как п > 0 и п' > 0, то фокусные расстояния оптической системы всегда имеют разные знаки. Как правило, для характеристики оптической системы используют заднее фокусное расстояние, поэтому, если f' > 0, то система считается положительной, если f' < 0, то - отрицательной. В отрицательных системах задний фокус находится перед оптической системой.
Фокусы, фокальные плоскости, главные плоскости, главные точки и фокусные расстояния называют кардинальными элементами оптической системы.
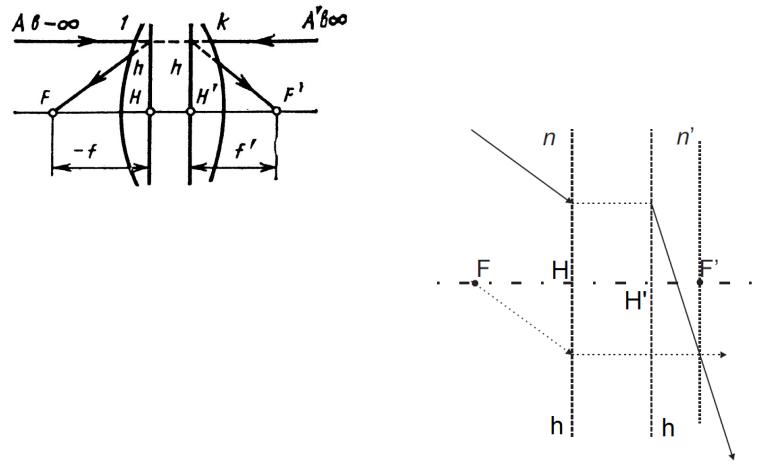
Положения фокусов и главных плоскостей определяют путем расчета или графического построения хода лучей, параллельных оптической оси, в прямом и обратном направлениях. Как следует из рис., при высоте h падения лучей в прямом и обратном ходе получаем следующие
формулы для определения фокусных расстояний: |
f ' h / tg 'k ; f h / tg 1 |
|
Схема для определения фокусных расстояний |
|
а – заднего, б – переднего |
4.5. Параксиальная область оптической системы. Параксиальные и нулевые лучи
Параксиальные лучи - лучи, образующие малые углы и ' с оптической осью и малые углы и ' с нормалью к преломляющей поверхности,
Параксиальная область - область в окрестности оси, внутри которой распространяются эти лучи. Углы и ' для параксиальной области обозначают и '.
Нулевой луч - фиктивный луч, преломляющийся (отражающийся) так же, как и параксиальный, на поверхностях, но встречающийся с ними на конечных расстояниях от оптической оси и отсекающий на оптической оси те же отрезки, что и параксиальный луч.
Формулы для расчета хода нулевого луча:
tg |
k 1 |
|
nk |
tg |
k |
h |
nk 1 |
nk |
; |
|
(48) |
||
|
|
|
|
||||||||||
|
|
nk 1 |
k |
nk |
1rk |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
hk 1 hk dk tg k 1. |
|
|
|
|
|
|
|||||||
Формула радиуса для вычисления |
радиусов |
rk |
|
|
nk 1 |
nk |
(49 |
||||||
поверхностей при заданном ходе луча: |
|
|
|
|
|
nk 1tg k 1 nk tg k |
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Параксиальное приближение позволяет определить следующие соотношения для углов прохождения луча
Закон Снелиуса в параксиальном приближении:
Введем обозначение:
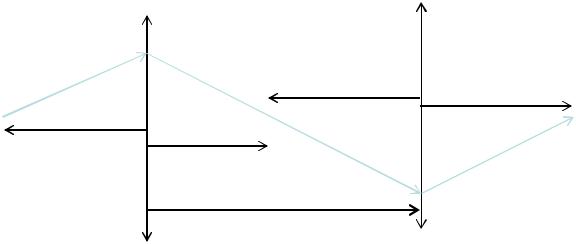
Прохождение лучей через многолинзовую систему
|
L1 |
|
|
|
L2 |
|
|
|
u1 |
h1 |
u’1 |
|
l2 |
|
|
l’ |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u2 |
|
|
|
|
u’ |
l1 |
|
|
|
|
h |
|
|
2 |
|
l’1 |
|
|
2 |
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
d1
Угол падения для последующего элемента равен выходному углу предыдущего элемента:
Расстояние до изображения с учетом дистанции между поверхностями (тонкими линзами) является расстоянием до объекта для следующей поверхности:
ui 1 ui'
li 1 li di
Высота изображения для предыдущей поверхности с
учетом угла и расстояния трансформируется в hi 1 hi diui входную высоту для следующей поверхности:
