Лекции прикладная оптика / Lec6_2015

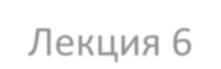
Лекция 6

АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ

Аберрации - погрешности изображений, обусловлены отклонениями лучей от тех направлений, по которым они должны были бы идти в идеальной оптической системе.

Геометрические и волновыми аберрациями - отклонения от первого условия Максвелла.

Геометрические аберрации описывают смещения (относительно геометрически идеальных положений) точек пересечения лучей с поверхностью изображения.

Волновые аберрации характеризуют ОРХ реального волнового фронта и идеального сферического.

Объективы, полностью удовлетворяющие первому условию Максвелла, называются

стигматическими.

Совершенные (в смысле стигматичности) объективы существуют, но, в общем случае, это возможно только для пары осевых сопряженных точек.

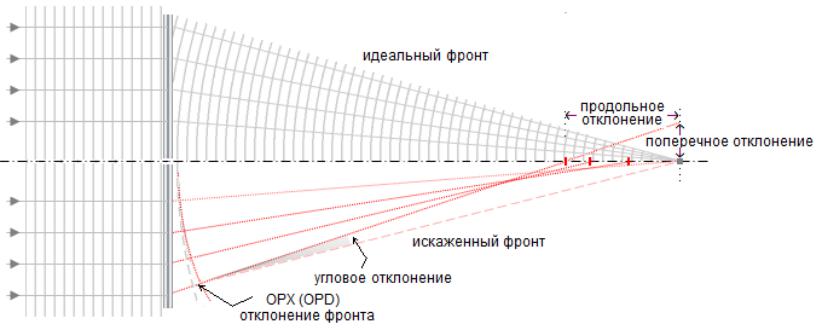
Пусть объектив стигматичен для сопряженных точек А и А'.

Если требуется стигматичность и для другой сопряженной пары точек В и В', то объектив должен удовлетворять условию Гершеля ndz sin2 (u / 2) n'dz'sin2 (u'/ 2).

Чтобы объектив был стигматичным для внеосевой пары точек С и С', он должен удовлетворять условию синусов Аббе ndysin u n'dy'sin u'.

В общем случае эти два условия адекватно и одновременно не выполнимы, кроме случая, когда u u' , т.е. для единичного увеличения.

Объектив, удовлетворяющий этому условию и стигматичный для точек на оси, называется апланатическим; он имеет вполне удовлетворительное качество изображения вблизи оси.

В параксиальной области, где sin u u и sin u' u' , условия Гершеля и Аббе выполняются одновременно, т.е. параксиальная модель оптической системы идентична идеальному стигматическому объективу.

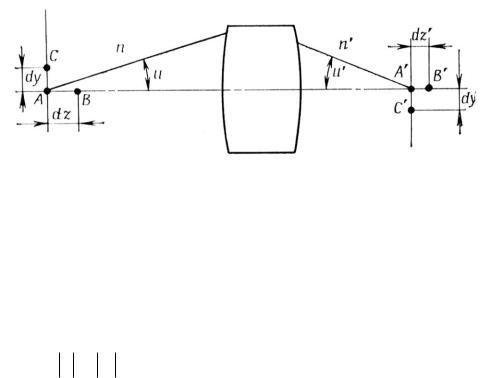
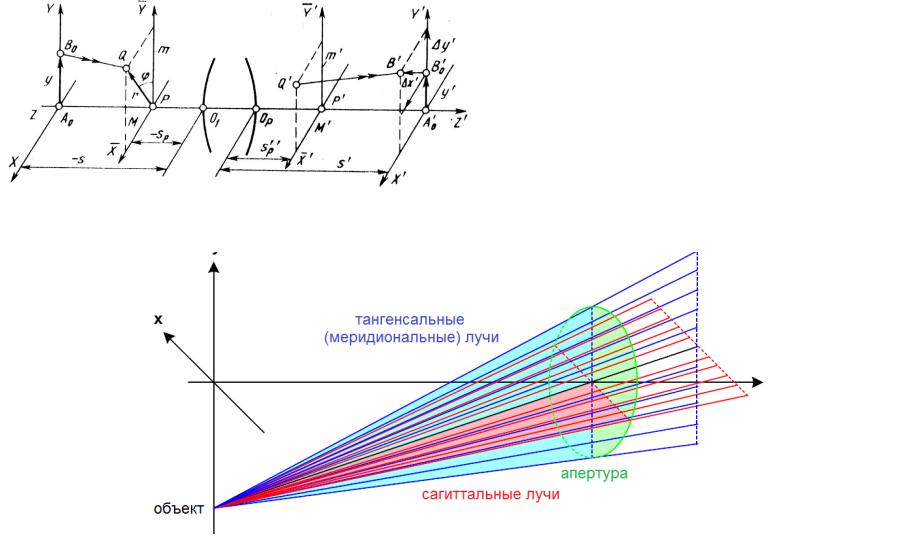
При наличии аберраций в системе некоторый луч, исходящий из внеосевой точки выходного зрачка ( ', '), минует точку (0, h') и попадает на поверхность изображения, например, в точке ( x', h'+ y').

определяемыми аберрационными полиномами, представляющими собой сумму произведений постоянных коэффициентов и степенных функций величин ', ', h'.

Описание аберраций

Оптические аберрации характеризуются величиной, на которую отклоняется построенный геометрически луч от нужного положения на изображении, формируемом оптической системой. Обычно нужное положение луча на изображении - это положение, определяемое гауссовыми законами первого порядка формирования изображения.

В связи с тем, что реальная оптическая система нарушает гомоцентричность лучей, в общем случае внемеридиоиальный луч, вышедший из точки В0, после оптической системы в точку В'() не приходит, а пересекает плоскость идеального изображении в точке В'. Тогда геометрической аберрацией будет отрезок

B'0B'.

Проекции аберраций на две плоскости:

меридиональную y' и сагиттальную х'.

Численное описание аберраций. Многочлен волновой аберрации

Численное описание аберрации удобно представить в виде разложения в зрачковых координатах.

Наиболее распространенные виды разложения:

1)разложение в степенной ряд:

2)по ортогональным полиномам и полиномам Цернике.

Полиномы обычно записываются в нормированных координатах.

Параксиальная высота h' нормируется следующим образом:

где u рмакс - половина угла поля зрения системы.

При записи полиномов применяются полярные координаты. Выразим зрачковые координаты ( ', ') через r' и :

' r'sin , ' r'cos

Если Dp - диаметр выходного зрачка, нормированными полярными координатами зрачка будут ( , ), где

2r' .

D' p

Численное описание аберраций. Многочлен волновой аберрации

Для графического представления аберрационных характеристик используются нормированные декартовы координаты зрачка (X, Y):

Аберрационные полиномы могут быть образованы двумя рядами членов вида:

a cbc H a b cosc ,

где a cbc - аберрационный коэффициент, а сумма а + b (всегда нечетная) - порядок аберрации.

Общий вид выражения для x', y' :

x' 0 a cbc H a b cosc sin ,y' 0 a cbc H a b cosc cos

где 0 1/(2n'sin u') . Правило знаков: угол и' считается положительным.

Численное описание аберраций. Многочлен волновой аберрации

При записи полиномов применяют полярные координаты.

Если аберрации изображения оптической системы выражаются как оптическая разность хода (ОРХ), то из условия симметрии оптическую разность хода можно выразить как разложение в ряд:

где W2l n,2m n,n - числовой коэффициент волновой аберрации;

h - высота изображения;

, - полярные координаты точки пересечения луча с входным зрачком системы; l, m, n - текущие индексы (положительные целые числа 0, 1, 2, 3, …).

Порядок определяется выражением [(2l + п) + (2т + п) - 1]. Эта сумма всегда нечетная.

Численное описание аберраций. Классификация геометрических аберраций

Геометрические аберрации подразделяются на классы в зависимости от их порядка: 1-го порядка , 3-го порядка, 5-го порядка и т. д.

Разные типы аберраций не одинаково влияют на качество изображения.

В рамках введенных Линфутом критериев оценки качества изображения аберрации, обладающие круговой или ортогональной симметрией, влияют на «структурное содержание» изображения, но не на его «правдоподобие». Асимметричные же аберрации даже в пределах допуска с точки зрения критерия структурного содержания сильно влияют на правдоподобие изображения. Такое понимание влияющих факторов, исходя из конечных целей использования данной системы, весьма существенно, поскольку в процессе расчета объектива возможна взаимная компенсация отдельных типов аберраций. Различия же во влиянии разных типов можно показать уже на примере аберраций 1-го и 3-го порядков.

Аберрации оптических систем делят на монохроматические и хроматические.

Монохроматическими аберрациями называют погрешности изображения, которые имеют место для лучей определенной длины волны.

Хроматические аберрации - при прохождении через преломляющие поверхности излучения сложного спектрального состава оно разлагается на составные спектральные части вследствие дисперсии света. В этом случае изображение представляет собой сумму большого числа монохроматических изображений, которые не совпадают между собой ни по положению, ни по размерам. Изображение становится окрашенным.

Численное описание аберраций. Классификация геометрических аберраций

первый порядок

1) хроматизм положения;

2) вторичный спектр;

3) хроматизм увеличения.