Лекции прикладная оптика / Lec4_2015
.pdf
Лекция 4
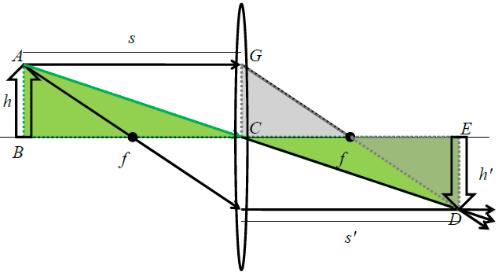
Понятие тонкой линзы:
•расстояние между главными плоскостями пренебрежимо мало;
•преломление всех лучей происходит на «одной «поверхности;
•луч не изменяет своего вертикального положения при прохождении линзы
•радиус кривизны много больше чем толщина линзы
Понятие тонкой линзы не равносильно параксиальному приближению и определениям.
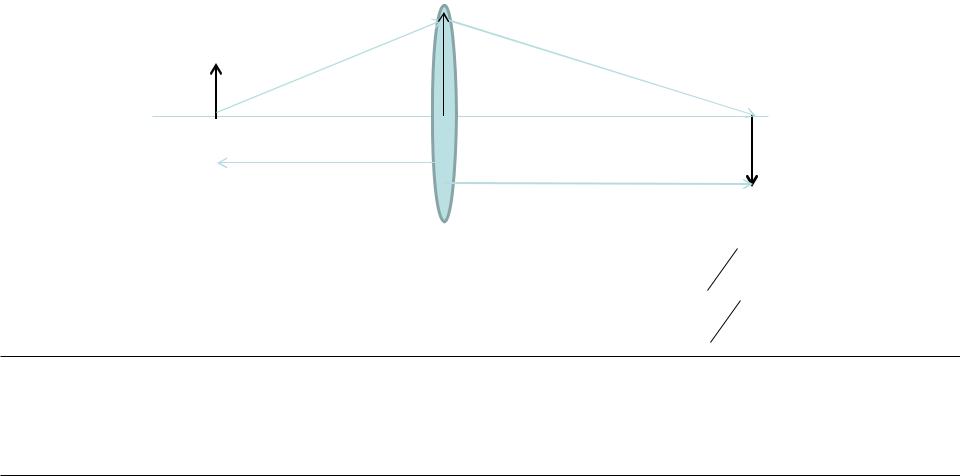
Рассмотрим прохождение «апертурного луча» через тонкую линзу.
Апертурный луч – это луч, идущий из осевой точки предмета и проходящий через край апертурной диафрагмы или самой линзы. АЛ определяет луч, который может пройти через систему под максимальным углом.
n n’
h
y u
Объект
l
Используя выражение для линейного увеличения М, и заменяя l, l’ используя определения of u, u’ получаем:
|
|
|
|
|
u’ |
|
Изображение |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l’ |
|
|
|
|
|
|
|
|
y’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nl |
|
|
n h |
|
|
|
|
nu |
|
|
||
M |
|
|
u |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
n |
h |
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
n l |
|
|
u |
|
n u |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнивая полученные выражения через M, получаем:
y |
M |
nu |
|
|
|
|
|
|
|
|
|
|
|
||||
y |
|
|
nuy n u y |
|
||||
|
n u |
|
|
|
|
|
||
Это значение постоянно для любого сечения в |
|
|
|
оптической системе и называется оптическим |
H nuy |
инвариантом или инвариантом Лагранжа. |
|
|
|
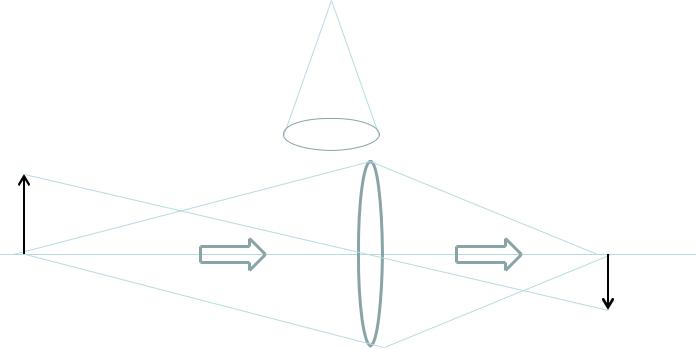
Телесный угол: 2 1 cosθ |
|
|
|
|
2 |
||
|
|
|
|
A h2 |
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
A |
h |
|
h |
|
|
|
u’ Изображение |
||
u |
|
|
|
|||
Объект |
u |
2 |
|
|
h’ |
|
|
|
|
|
|||
(светимость = R) |
|
|
u |
2 |
|
|
|
|
|
|
|
||
Мощность излучаемая на линзу:
|
В предположении отсутствия |
RA P R A |
потерь в системе. |
|
Увеличение: |
m |
h |
|
|
u |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
Инвариант Лагранжа: |
||||||||
|
|
|
h |
u |
|
|
|
|
|
uh u h |
|||||
|
|
|
|
|
|
|
|
|
|||||||
Следовательно: |
|
|
|
u |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
m |
|
|
m |
|
|
|
|||||||||
h mh, |
u |
A |
A, |
m2 |
A A |
||||||||||
Следовательно:
R R
СВЕТИМОСТЬ ИЗОБРАЖЕНИЯ РАВНА СВЕТИМОСТИ ОБЪЕКТА.
|
|
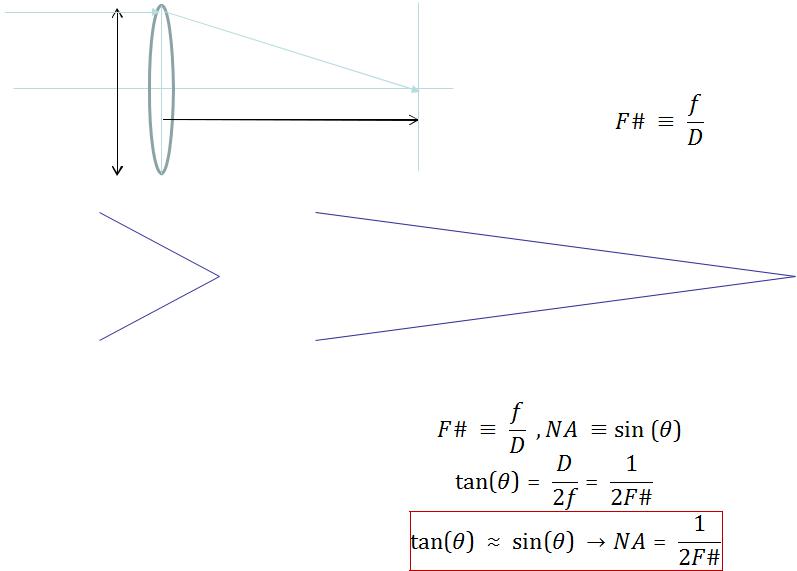
Относительное отверстие |
||
D |
θ |
или F-число в воздухе |
||
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
f = D |
|
f = 4D |
D |
|
D |
|
|
|
|
|
f/1 линза: “быстрая (fast)” |
f/4 линза : “медленная (slow)” |
|
Соотношение между F# и NA:
Освещенность изображения, образованного оптической системой, прямо пропорциональна квадрату ее относительного отверстия
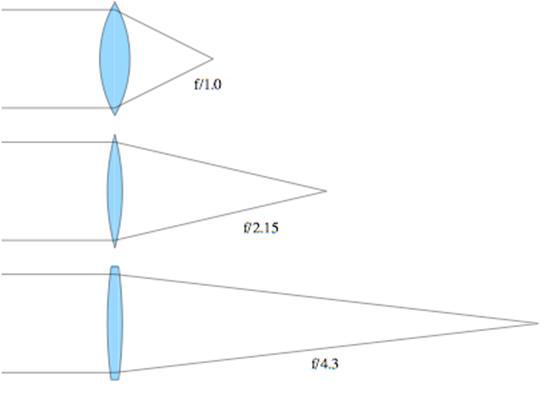
•Кривизна поверхности линз для стекла n = 1.5
–очевидно, что линзы с большим F-числом легче производить, потому что радиус кривизны меньше.
•F-число одна из основных характеристик линз и зеркал.
•Лиза с малым F-числом формирует «быстро» сходящийся пучок и
ееповерхность должна быть «идеальной».
•Медленно “slow” сходящийся луч проще формируется с хорошим качеством.
•Аберрации пропорциональны 1/(F#)2
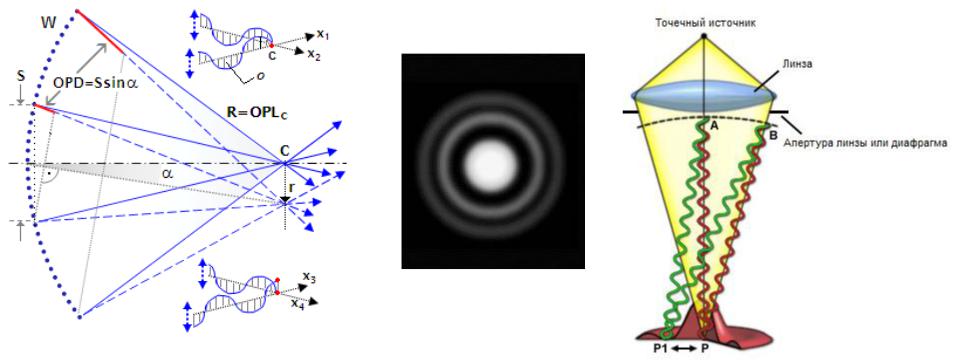
В реальной оптической системе ход лучей ограничивается диафрагмами, в качестве которых может выступать оправа оптического элемента. В общем случае, форма диафрагмы круглая, что приводит дифракции оптического излучения на круглом отверстии, которая формирует диск Эйри.
Одинаковые оптические пути соответствующие лучам приходящим в центр кривизны сферы, где расположен фокус, равны радиусу кривизны R волнового фронта, и лучи приходят в точку С со одинаковой фазой обеспечивая максимальную интенсивность. Лучи приходящие в другие точки на плоскости изображения имеют разные фазы, что уменьшает суммарную интенсивность. Это приводит к появлению четкого неискаженного центрального пятна с концентрическими кольцами уменьшающейся интенсивности.
ΔΦ = 2πOPD/λ = 2πSsinα/λ
В идеальной оптической системе точка изображается в виде точки, а в реальной оптической системе точка изображается в виде пятна рассеяния.
Основной характеристикой, описывающей передачу структуры предмета оптической системой является функция рассеяния точки.
Функция рассеяния точки (ФРТ, point spread function, PSF)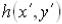 
– это функция,
описывающая зависимость распределения освещенности от координат в плоскости изображения, если предмет – это светящаяся точка в центре изопланатической зоны.
|
|
|
|
2 |
|
2 |
||
|
2J1 |
|
|
|
a sin( ) |
|
||
|
||||||||
I I0 |
|
|
|
|
|
|||
|
2 |
|
||||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
a sin( ) |
||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
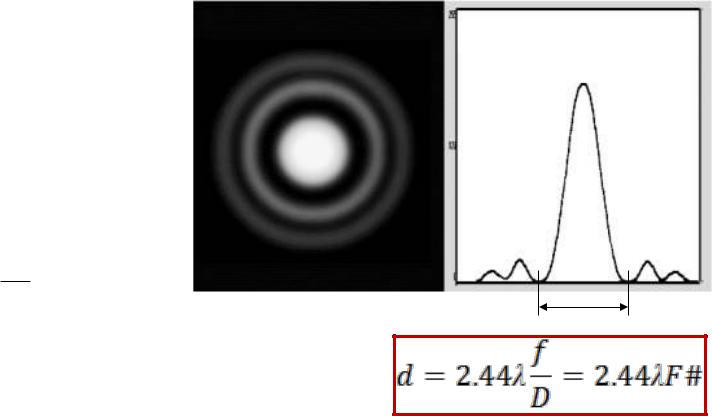
Первая темная полоса по расположена под углом к оси:
1.22 2a
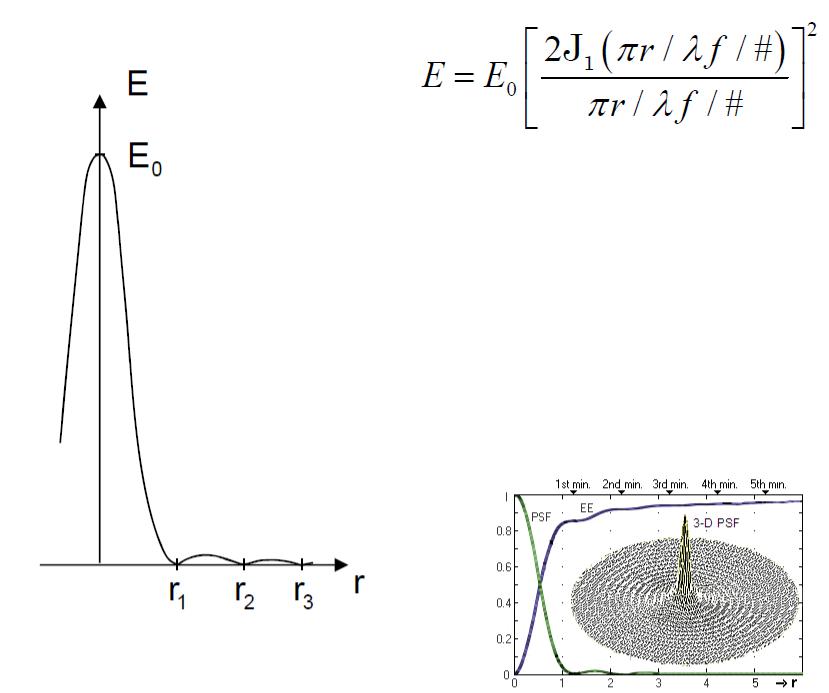
d
Следовательно, линза с фокусом f и диаметром D, формирует изображение точки в виде диска Эйри, с первым темным пятном имеющим радиус :
|
Радиус |
Пик |
% энергии в |
|
|
энергии |
кольце |
|
|
|
|
Центральный |
0 |
1.0 E0 |
83.9 |
максимум |
|
|
|
Первый минимум |
1.22λF# |
0 |
|
|
|
|
|
Первое кольцо |
1.64λF# |
0.017 E0 |
7.1 |
Второй минимум |
2.24λF# |
0 |
|
Второе кольцо |
2.66λF# |
0.0041 E0 |
2.8 |
Третий минимумум |
3.24λF# |
0 |
|
|
|
|
|
Третье кольцо |
3.70λF# |
0.0016 E0 |
1.5 |
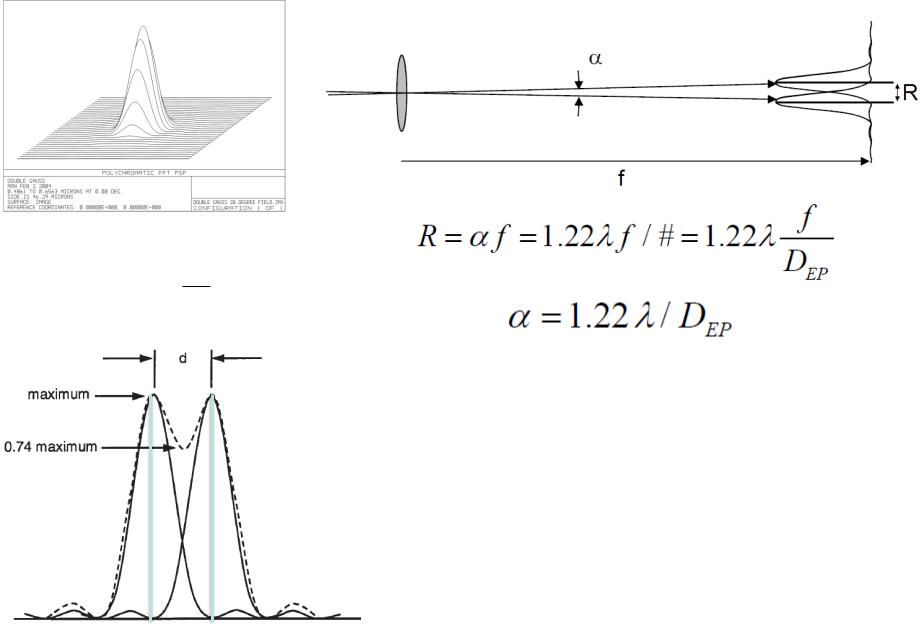
Размер изображения точки в идеальной (без аберрационной ) оптической системе определяется дифракцией излучении на границе апертуры.
FWHM = 1.02 F#
FWHM 1.02 D
Если расстояние между максимумами двух дифракционных изображений одинаковых точек равно радиусу диска Эйри, и суммарная интенсивность в точке половине радиуса равна 0.74 от интенсивности пика , то
эти две точки различимы. Выполнение указанных
условий определяет критерий Релея для разрешения близлежащих точек.