Лекции прикладная оптика / Lec12_2015

Распространение света в прозрачных средах

При любом числе соприкасающихся сред с параллельными границами раздела произведение показателя преломления вещества на синус угла, образованного лучом с нормалью к поверхности, остается постоянным:

n1 sin 1 n2 sin 2 ... nm sin m .

Если показатели преломления первой и последней сред одинаковы (например, воздух), то лучи, входящий в систему и выходящий из нее, параллельны между собой.

Отражение света – явление, заключающееся в том, что при падении света (оптического излучения) из первой среды на границу раздела со второй средой взаимодействие света с веществом приводит к появлению световой волны, распространяющейся от границы раздела обратно в первую среду. При этом по крайней мере первая среда должна быть прозрачна для падающего и отраженного излучения.

Диффузное отражение света – его рассеивание неровной поверхностью второй среды по всем возможным направлениям. Пространственное распределение отраженного потока излучения и его интенсивность различны в разных конкретных направлениях и определяются соотношением между длиной волны и размерами неровностей, распределением неровностей по поверхности, условиями освещения, свойствами отражающей среды.

Пространственное распределение диффузно отраженного света приближенно описывается законом Ламберта. Диффузное отражение света наблюдается также от сред, внутренняя структура которых неоднородна, что приводит к рассеянию света в объеме среды и возвращению части его в первую среду. И поглощение, и рассеяние света во второй среде могут сильно зависеть от .

9.1. Распространение света в прозрачных средах

Зеркальное отражение света отличает определенная связь положений падающего и отраженного лучей:

1)отраженный луч лежит в плоскости, проходящей через падающий луч и нормаль к отраженной поверхности;

2)угол отражения равен углу падения.

I R T

Распространение света в прозрачных средах

Свет, отраженный под углом, всегда хотя бы частично поляризован. Состояние поляризации отраженного и преломленного света зависит от состояния падающего.

Ее - амплитуда падающего света

Составляющие Ее:

Ер – лежащая в плоскости падения р-составляющая

Еs – лежащая в плоскости, перпендикулярной к ней s-составляющая.

Распространение света в прозрачных средах

Соотношения между амплитудами и фазами падающей, отраженной и прошедшей волн определяются формулами Френеля:

где Rs и Rр – коэффициенты отражения; Тs и Тр – коэффициенты пропускания s- и р-составляющих отраженного и проходящего света; n1 и n1 – показатели преломления граничащих сред); 1 – угол падения в первой среде, 2 – угол преломления во второй среде.

Формулы Френеля служат для расчета амплитуд и интенсивностей отраженного и проходящего света на плоской границе раздела двух диэлектриков. Они позволяют рассчитать амплитуды и интенсивности при различных углах падения.

Из формул следует, что если падающая волна поляризована произвольным образом, то поляризации отраженной и преломленной волн будут отличаться от поляризации падающей волны.

Распространение света в прозрачных средах

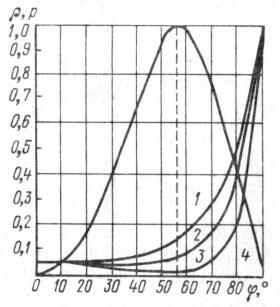
Зависимость коэффициентов отражения и степени поляризации р пучка от угла падения :

1 – электрические колебания перпендикулярны плоскости падения (s-компонента);

2 – естественный свет; 3 – электрические колебания параллельны плоскости падения (р-

компонента); 4 – степень поляризации отраженного пучка

Изменение коэффициента отражения различно поляризованных компонент излучения при падении волны на границу раздела двух прозрачных сред – воздуха и стекла, причем n n1 .

При падении света по нормали 1 2 , разница между rs и rр исчезает и, если амплитуду

падающего света принять равной единице, то коэффициенты Френеля могут служить характеристиками амплитуд отраженного и преломленного лучей, поскольку при падении света по нормали понятие о плоскости падения теряет смысл:

9.1. Распространение света в прозрачных средах

Интенсивность света (коэффициент отражения), отраженного от поверхности прозрачной среды:

n 1 2 R 2n2 1

будет тем выше, чем выше показатель преломления n2 этой среды.

Формулы Френеля справедливы также для случая поглощающих сред. При этом достаточно в выражениях действительные значения показателей преломления сред заменить соответствующими комплексными величинами. В таком случае амплитуды отраженной и преломленной волн, а также угол преломления становятся комплексными.

Распространение света в прозрачных средах

При решении вопросов прохождения и отражения света в системе нескольких соприкасающихся сред пронумеруем среды, амплитуды и другие характеристики в порядке прохождения их светом. Тогда амплитудные характеристики rs и rр будут иметь дополнительные номера тех сред, из которых выходит и куда направляется луч.

амплитуды s- и р-составляющих для света, идущего из среды с номером (k-1) в среду с номером k. Обобщенные амплитуды будут определяться соответствующими выражениями:

9.1. Распространение света в прозрачных средах

Эти выражения дают возможность судить об амплитуде и фазе отраженной волны.

При n1 cos 2 n2 cos 1, 1 2 2 , rp 0, в то время как rs 0 .

Закон Брюстера:

tg B n2 n1

В этом случае отраженный свет полностью поляризован и колебания расположены в плоскости, перпендикулярной к плоскости падения. В проходящем свете полная поляризация невозможна. Наблюдается частичная поляризация, преимущественно за счет колебаний, лежащих в плоскости падения (р).

Распространение света в прозрачных средах

При наклонном падении излучения на плоскую границу происходит достаточно детерминированное искажение состояния поляризации потока излучения. В случае падения естественного света, у которого мощность обеих составляющих одинакова, отраженный поток будет характеризоваться определенной степенью поляризации.

Степень поляризации отраженного потока

Степень поляризации проходящего излучения