2.2. Кинематика входных механизмов

2.2.1. Кривошип

Термин “кривошип” здесь применяется для краткости. Рассматривается любое вращающееся звено, имеющее кинематическую пару со стойкой (рис. 2.1). Координаты точки А конца кривошипа в неподвижной системе X₀,Y₀:

x_A = l_ОА cos ₀₁ , y_A = l_ОА sin ₀₁

где l_ОА – длина кривошипа.

Скорость точки А: v_A = ₁ l_ОА,

а её проекции: v_Ax = – ₁ l_ОА sin ₀₁,

v_Ay = ₁ l_ОА cos ₀₁ .

Ускорение точки A имеет две составляющие: нормальную, характеризующую изменение вектора скорости по направлению и касательную, характеризующую изменение вектора скорости по величине:

Проекции составляющих ускорения, соответственно

2.2.2. Ползун

Ось входного ползуна (рис. 2.2) в общем случае может составлять с осью X₀ НСК некоторый угол ₀₁. Для определения положения точки A должны быть заданы два конструктивных параметра: l₀ – расстояние от места крепления цилиндра до положения поршня, в котором ход штока считается равным нулю и lш – длина штока. Параметром, определяющим положение поршня, будем считать его ход S. Тогда координаты точки A, проекции её скорости и ускорения на оси неподвижной системы координат определятся следующими очевидными соотношениями.

x_A = l_OA cos ₀₁, y_A = l_OA sin ₀₁,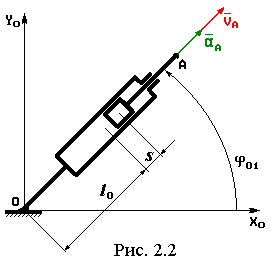

v_Ax = v_A cos ₀₁, v_Ay = v_A sin ₀₁,

a_Ax = a_A cos ₀₁, a_Ay = a_A sin ₀₁,

где l_OA = l₀ + S + lш.

2.2.3. Качающийся ползун

В отличие от предыдущих – данный механизм (рис. 2.3) имеет 2-й класс. Для получения расчетных зависимостей воспользуемся методом векторных контуров, предложенным В.А. Зиновьевым [5, 9, 14, 18].

При решении задачи кинематического анализа этим методом, звенья механизма представляют в виде векторов. Поскольку в данном случае механизм замкнут через стойку, то они образуют замкнутые контуры. Составляют векторные уравнения замкнутости контуров, проецируют их на оси координат, получая системы алгебраических уравнений для определения кинематических параметров, характеризующих положение звеньев. Последовательно дифференцируя эти зависимости по времени, получают уравнения для определения скоростей и ускорений.

Получим решения для двух вариантов механизма, показанных на рис. 2.3.

Решение для варианта механизма, изображённого на рис. 2.3а.

Звено OAP, в общем случае может быть не прямым, а иметь “слом”, характеризующийся углом  (см. рис. 2.3). Обобщенной координатой является перемещение звена 2 относительно звена 1, обозначим его S. Уравнение замкнутого векторного контура:

(2.1)

Проецируя его на оси X₀Y₀ имеем:

l11 cos 11 + l12 cos 12 – l21 sin 2 + l22 cos 2 + l23 sin 2 – l3x = 0

(2.2)

l11 sin 11 + l12 sin 12 +l21 cos 2 + l22 sin 2 – l23 cos 2 – l3y = 0

Для получения явного решения этой системы рассмотрим схемы на рис. 2.4, 2.5 и найдем сначала решение в случае, когда отсутствует “слом” в точке A и смещения BC и DE. Решение будем искать в системе координат OXY, естественной для данного механизма.

Запишем уравнения окружностей: первая радиусом OB с центром в начале координат, вторая радиусом BE с центром в шарнире E:

(2.3)

Отсюда получаем координаты шарнира B в системе OXY:

(2.4)

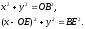
где ,x_E, y_E – координаты опоры Е в системе OX₀Y₀.

Двузначность в выражении для y_B указывает на наличие двух сборок механизма. Сборку, показанную на рис. 2.4 принято называть прямой, ей соответствует знак плюс, а показанную на рис. 2.5 – обратной, ей соответствует знак минус. Тогда, углы поворота звеньев ОВ и СЕ в системе OXY:

( 2.5 )

Углы поворота этих звеньев в системе OX₀Y₀ при отсутствии “слома” и смещений:

( 2.6 )

2.6 )

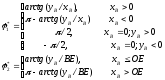
При наличии “слома” и смещений:

₁₁ = ₁ +  = ₁ + arcsin(sin  (l₁₂/l₁)),

₂ = ₂₀ + arcsin((DE – l₂₁)/BE).

Продифференцируем систему (2.2) по времени:

–l₁₁₁ sin₁₁ + v₁ cos₁₂ – l₁₂ ₁ sin₁₂ – l₂₁ ₂ cos₂ – l₂₂ ₂ sin ₂ + l₂₃₂ cos₂ = 0

l₁₁₁ cos₁₁ + v ₁ sin ₁₂ + l₁₂₁ cos₁₂ – l₂₁ ₂ sin ₂ + l₂₂ ₂ cos₂ + l₂₃ ₂ sin₂ = 0

(2.7)

где

– обобщенная скорость.

Отсюда находим угловые скорости ₁, ₂.

Дифференцируя систему (2.7) и приводя подобные члены получим уравнения для определения угловых ускорений 1, 2 :

(2.8)

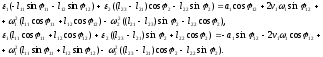
где – обобщенное ускорение.

Отсюда находим угловые ускорения ₁, ₂.

Величину l₁₂ удобно разделять на две части: 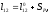где– длина АВ, когда рабочий ход входного ползуна S_P = 0 .

Решение для варианта механизма, изображённого на рис. 2.3б. будем искать в системе координат OXY, естественной для данного механизма.

Контур OAC, содержащий рабочий ползун, в общем случае может иметь смещения l₁₁, l₂₂ (см. рис. 2.3), что влияет на величину угла ₂₁. Обобщенной координатой этого механизма является перемещение звена 2 относительно звена 1, обозначим его S. Тогда длина вектора l_S = l₀ + S, где l₀ – расстояние от точки A до того положения ползуна P, в котором S = 0.

Для получения явного решения рассмотрим OCB. В нем известны длины всех сторон, так как l₂ = (l_S + l₂₁) cos, где  = arcsin((l₂₂ – l₁₁)/(l_S + l₂₁)) – угол, между векторами l₂ и l₂₁. Если обозначить p – полупериметр OCB, то

₂ = 2arctg(r/(p – l₃₂)); ₂₁ = ₂  ; ₃ = 2arctg(r/(p – l₂));

где .

Знак “+” в выражениях для ₂ и ₂₁ соответствует прямой сборке механизма, изображенной на рис. 2.3, а знак “–” – для обратной, когда точка C располагается ниже оси X. Угол ₃₂ = 2 – ₃ – для прямой сборки, и ₃₂ = ₃ – для обратной.

Для нахождений угловых скоростей ₂₁, ₃₂ и ускорений ₂₁, ₃₂ запишем уравнение замкнутого векторного контура:

(2.1*)

Проецируя его на оси системы OXY имеем:

– l₁₁ sin ₂₁ + l_S2 cos ₂₁ + l₂₂ sin ₂₂ + l₃₂ cos ₃₂ – l₄ = 0;

(2.2*)

l₁₁ cos ₂₁ + l_S2 sin ₂₁ – l₂₂ cos ₂₂ + l₃₂ sin ₃₂ = 0,

где l_S2=l_S+l₂₁.

Продифференцируем систему (2.2*) по времени:

l₁₁_S2 cos ₂₁ + v_S2 cos₂₁ – l_S2 _S2 sin₂₁ + l₂₂ _S2 cos₂₁ – l₃₂ ₃ sin ₃₂ = 0

– l₁₁_S2 sin ₂₁ + v_S2 sin ₂₁ + l_S2 _S2 cos₁₂ + l₂₂ _S2 sin ₂₁ + l₃₂ ₃ cos ₃₂ = 0

(2.3*)

где

– обобщенная скорость.

Отсюда находим угловые скорости ₂, ₃.

Дифференцируя систему (2.3*) и приводя подобные члены получим уравнения для определения угловых ускорений ₂, ₃ :

_S2 (l₁₁ cos ₂₁ – l_S2 sin ₂₁ + l₂₂ cos ₂₁) – l₃₂ ₃ sin ₃₂ =

= l₁₁_S2² sin ₂₁ – a_S2 cos ₂₁ + 2v_S2 _S2 sin ₂₁ + l_S2 _S2² cos ₂₁ + l_S2 _S2² sin ₂₁ +

+ l₃₂ ₃² cos ₃₂,

_S2 (–l₁₁ sin ₂₁ + l_S2 cos ₂₁ + l₂₂ sin ₂₁) + l₃₂ ₃ cos ₃₂ =

= l₁₁_S2² cos ₂₁ – a_S2 sin ₂₁ – 2v_S2 _S2 cos ₂₁ + l_S2 _S2² sin ₂₁ – l_S2 _S2² cos ₂₁ +

+ l₃₂ ₃² sin ₃₂,

_S2 ((l₁₁ + l₂₂) cos ₂₁ – l_S2 sin ₂₁) – l₃₂ ₃ sin ₃₂ =

= (l₁₁_S2 + 2v_S2 + l_S2 _S2) _S2 sin ₂₁ + (– a_S2 + l_S2 _S2² ) cos ₂₁ + l₃₂ ₃² cos ₃₂,

_S2 ((l₂₂ – l₁₁) sin ₂₁ + l_S2 cos ₂₁) + l₃₂ ₃ cos ₃₂ =

= (l₁₁_S2 – 2v_S2 – l_S2 _S2) _S2 cos ₂₁ + (– a_S2 + l_S2 _S2²) sin ₂₁ + l₃₂ ₃² sin ₃₂,

(2.4*)

где

– обобщенное ускорение.

По найденным ₂₁, ₃₂, _S2, ₃, _S2, ₃ методом преобразования координат, описанным в следующей главе, можно определить параметры движения любых точек на звеньях входных механизмов, в частности тех, в которых к ним присоединяются структурные группы. Эти величины и будут входными кинематическими параметрами для расчета структурных групп.