6.2. Уравновешивание роторов

Ротор – это вращающееся звено, установленное в неподвижных опорах. Примерами роторов являются коленчатые валы двигателей внутреннего сгорания и дизелей, распределительные валы, роторы электродвигателей, турбин, колеса транспортных средств и т.п.

6.2.1. Уравновешивание роторов при известном расположении неуравновешенных масс

Данная задача возникает и решается на этапе проектирования ротора. На рис. 6.2а изображен некоторый вал, на котором расположены две неуравновешенные массы. На данном примере легко пояснить физический смысл статической неуравновешенности, который состоит в том, что центры масс деталей, установленных на роторе смещены, относительно оси вращения и, как следствие, центр масс всего ротора тоже может быть смещен относительно этой оси. Таким образом, задачей статического уравновешивания в данном случае будет расчет и установка противовеса, так, чтобы центр масс всего ротора оказался на оси его вращения.

На рис. 6.2б представлена расчетная схема, где m₁, m₂ – величины неуравновешенных масс, r₁, r₂ – радиусы расположения центров масс деталей, установленных на роторе. Вид с торца вала на систему показан на рис. 6.2в. Поскольку конструкция ротора известна, то значения m₁, m₂, r₁, r₂ могут быть рассчитаны, и мы их полагаем известными.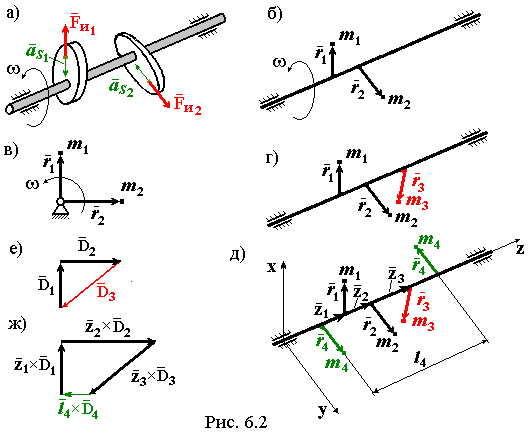

Статическое уравновешивание. Исходным условием статической уравновешенности является равенство нулю суммы всех сил инерции:

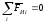
( 6.2 )

Из этого условия, полагая, что ротор вращается равномерно, получаем:

Произведение m_i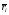массы на радиус-вектор в теоретической механике называют статическим моментом массы, отсюда и название статическое уравновешивание. В инженерной практике для этого произведения укоренился другой термин: дисбаланс. Таким образом, окончательно условие статической уравновешенности получаем в виде равенства нулю суммы дисбалансов масс: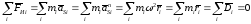

( 6.3 )

Собственно, статическое уравновешивание производится установкой противовеса. Для расчета его параметров построим план дисбалансов (см. рис. 6.2е). Замыкая контур, получаем вектор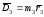

характеризующий параметры противовеса. Конкретное сочетание значений m₃,r₃, обеспечивающее нужный дисбаланс подбирается конструктивно. На рис. 6.2г изображён ротор с установленным противовесом, статически уравновешивающим ротор.

Моментное уравновешивание. Исходным условием моментной уравновешенности является равенство нулю суммы моментов всех сил инерции.

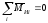
( 6.4 )

Введем систему координат XYZ (см. рис. 6.2д). Моменты сил инерции будем брать относительно начала координат этой системы:

Таким образом, окончательно условие моментной уравновешенности получаем в виде:

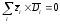
( 6.5 )

Установка еще одного противовеса вызовет нарушение статической балансировка. Поэтому поступают следующим образом. Из конструктивных соображений выбирают длину l₄и строят план векторных произведений в соответствии с условием (6.5). На рис. 6.5ж построен такой план для удобства, повернутый на 90^Опо направлению вращения ротора. Замыкая контур, получаем вектор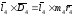

Моментное уравновешивание производится установкой двух одинаковых, противоположно направленных противовесов, разнесенных по длине вала на расстояние l₄, и создающих момент, компенсирующий момент сил инерции от других масс. На рис. 6.2д изображен ротор с установленными противовесами, уравновешивающими ротор моментно.

Таким образом, мы рассмотрели методику, по которой для полного уравновешивания требуется три противовеса. Эту методику можно считать наиболее общей. На практике же могут возникать и различные частные случаи.

Иногда удается произвести полное уравновешивание одним противовесом. Дополнительные два противовеса для моментного уравновешивания нам понадобились по тому, что план на рис. 6.2ж в общем случае оказывается не замкнут, что свидетельствует о наличии вредного момента сил инерции. Однако если мы имеем возможность менять место установки противовеса m₃на валу и место расположения хоты бы одной из массm₁, m₂то варьируя величинами, например,z₁,z₂можно сделать замкнутым контур. Удаётся это не всегда, так как при этом может оказаться, что противовесm₃ надо установить за пределами вала.

Вторым часто встречающимся на практике случаем является тот, когда уравновешивают каждую массу m₁, m₂отдельно, т.е. для каждой устанавливается свой противовес. Это может быть эффективно для небольшого количества неуравновешенных масс: 1 … 3, в противном случае это ведет к заметному утяжелению конструкции.