4.9.3. Определение реакций в опорах валов

Эту задачу решим на примере второго вала механизма, изображенного на рис. 4.21. На рис. 4.23 представлены расчетные схемы.

1. Разрываем кинематические пары зацепления колес 1-2 и 3-4 и в точках отсоединения прикладываем реакции отброшенных частей, которые в данном случае являются усилиями в зацеплениях (рис. 4.23а).

2. Приводя эти усилия к центрам колес, и полагая, что всю осевую нагрузку воспринимает подшипник B, получаем балку на двух опорах, нагруженную пространственной системой сил (рис. 4.23б).

Реакции в опорах A и B найдем из уравнений равновесия. Сначала найдем составляющие реакций, действующие в плоскостиXY.

Из условия F_X= 0 получаем R_Bx= F_X2– F _X3

Условие M_A^XY= 0 дает:

R_By(l₁+l₂+l₃) +F_r2l₁–F_r3(l₁+l₂) +M_X2+M_X3 = 0.

Откуда: R_By= (F_r3(l₁+l₂) – F_r2l₁–M_X2–M_X3) / (l₁+l₂+l₃).

Тогда из условия F_Y= 0 получаем:

R_Ay= F_r3– F_r2– R_By.

Теперь найдем составляющие реакций, действующие в плоскости XZ. УсловиеM_A^XZ= 0 дает:

R_Bz(l₁+l₂+l₃) –F_t2l₁+F_t3(l₁+l₂) = 0.

Откуда: R_Bz= (F_t2l₁–F_t3 (l₁+l₂)) / (l₁+l₂+l₃).

Тогда из условия F_Z= 0 получаем:

R_Az= F_t2– F_t3– R_Bz.

Полные реакции в опорах:

4.10. Кпд зубчатых механизмов

Подробный расчет КПД зубчатых механизмов не является задачей данного курса. Здесь мы рассмотрим лишь основные принципы. Более подробно этот вопрос рассмотрен, например, в работе [ 16 ].

Первое, что следует отметить – это то, что учет потерь на трение с помощью КПД представляет собой довольно грубую методику, применимую только для механизмов, имеющих достаточно высокую степень нагруженности внешними полезными силами, когда доля сил трения в общей силовой картине не высока. Это обычно характерно для машиностроения. В приборостроении, особенно в точном приборостроении, обычно применяют более тонкие методики.

4.10.1. Кпд зубчатых механизмов с неподвижными осями колес

Введем понятие коэффициента потерь:

( 4.38 )

где N_ТР– мощность сил трения,N_ВЩ– мощность на ведущем колесе.

Тогда КПД механизма можно представить в виде

 = 1 – ( 4.39 )

Общий коэффициент потерь механизма находят как сумму коэффициентов потерь от различных видов потерь_i:

 = _i

Рассмотрим основные виды потерь, характерные для зубчатых механизмов.

Потери на трение в зацепленияхобычно определяются по упрощенной эмпирической зависимости

_З2,3f _З(1/Z₁1/Z₂) ( 4.40 )

где f _З1,25f– коэффициент трения в зацеплении;

f– коэффициент трения скольжения, определяемый по номограммам, например, рис. 4.24 [16] в зависимости от степени нагруженности передачи и суммы скоростей контактирующих точек

v_2vsin_W,

где v– окружная скорость зубчатых колес;

Z₁,Z₂ – числа зубьев колес, знак “+” берется для внешнего зацепления, “–” – для внутреннего.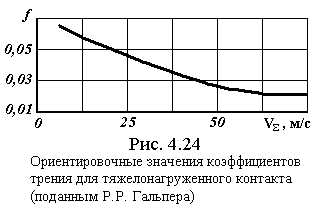

Потери на трение в подшипникахкачения определяют по формуле [ 16 ]

( 4.41 )

где M_ТРj, n_j– момент трения и частота вращенияj-го подшипника;n_П– количество подшипников в опоре (редукторе);(Mn)_РО– произведение момента и частоты вращения рабочего органа.

Приближенное значение момента трения определяют из зависимости

M _ТР = 0,5f F_r d

где f – коэффициент трения в подшипнике (см. [ 2 ]);

F_r– радиальная нагрузка на подшипник;

d– внутренний диаметр подшипника.

Потери на перемешивание и разбрызгивание масладля цилиндрических передач с внешним зацеплением, смазываемых окунанием при погружении зубчатого колеса на глубину (2…3)m, приближенно определяется по формуле [16]

( 4.42 )

где  – кинематическая вязкость масла при рабочей температуре, м²/с;

М₁– крутящий момент, Нм;

V – окружная скорость, м/с;

линейные размеры берутся в мм.

При струйной смазке значения _РМ, найденные по формуле (4.42) надо умножить на коэффициент 0,7.

Таким образом, общий коэффициент потерь для большинства зубчатых механизмов с неподвижными осями колес находят как сумму трех коэффициентов потерь:

 = _З +_П +_РМ.