Аналитическая геометрия дз 15 вариант

1. Составить уравнение кривой, сумма расстояний от каждой точки которой до точек и равна 10.

Решение.

Пусть точка принадлежит искомой кривой.

Расстояние от точки до точки :

Расстояние от точки до точки :

По условию задания

Точки и лежат на одной ординате. Следовательно, можно предположить по определению, что мы ищем уравнение эллипса, а точки и - это фокусы кривой.

Сместим начало отсчета в точку .

Расстояние между точками и равно , при этом согласно условию .

Перейдем к старой системе координат:

Ответ:

2. Привести уравнение к каноническому виду, определить тип кривой и ее эксцентриситет, изобразить ее на одном чертеже в старых и новых координатах.

а)

б)

Решение.

а)

Это уравнение параболы.

Эксцентриситет параболы равен 1.

б)

Обозначим

Матрица этой квадратичной формы имеет вид

Составим характеристическое уравнение матрицы

Откуда

Найдем собственные векторы. Для имеем систему уравнений

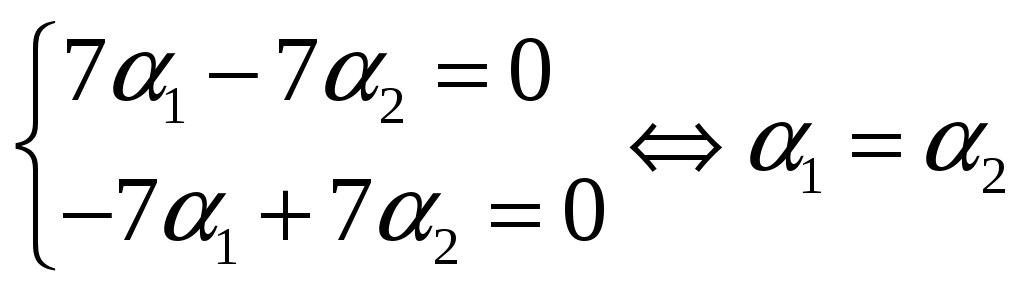
Тогда

Нормируя полученные векторы, находим

Для получаем систему

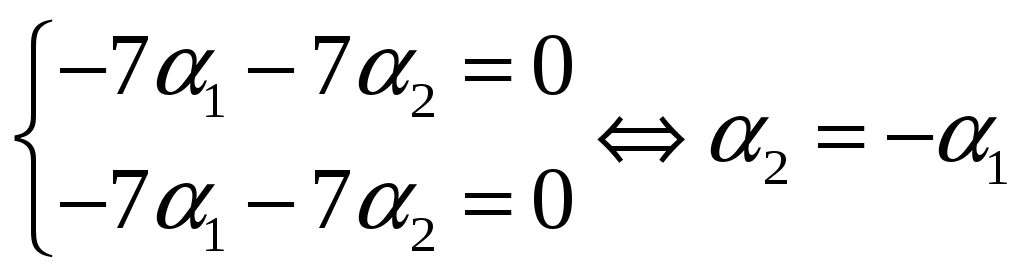
Следовательно,

Нормируя полученные векторы, имеем

Таким образом, матрица преобразования координат

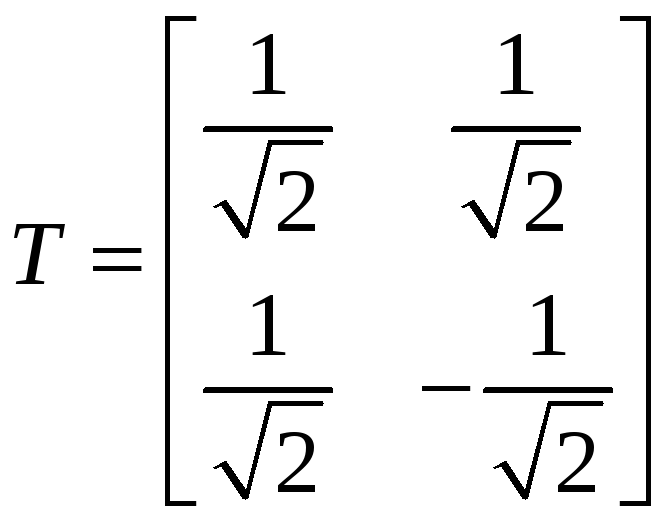
формулы преобразования осей координат имеют вид

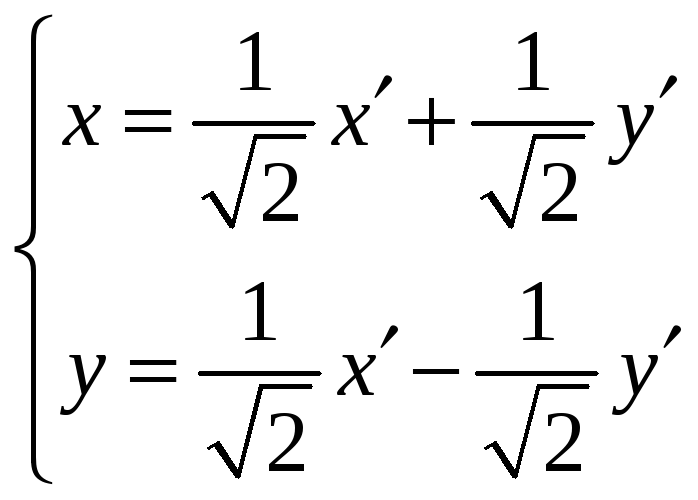(1)

Подставив в уравнение данной кривой выражения для x и y из (1), имеем

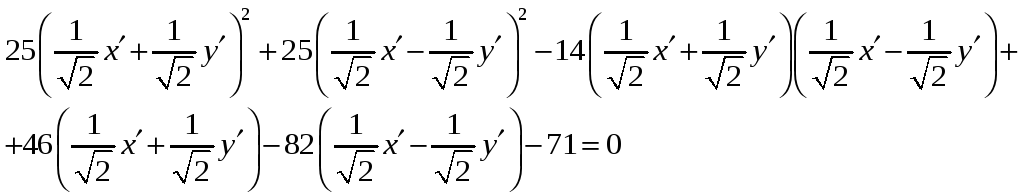
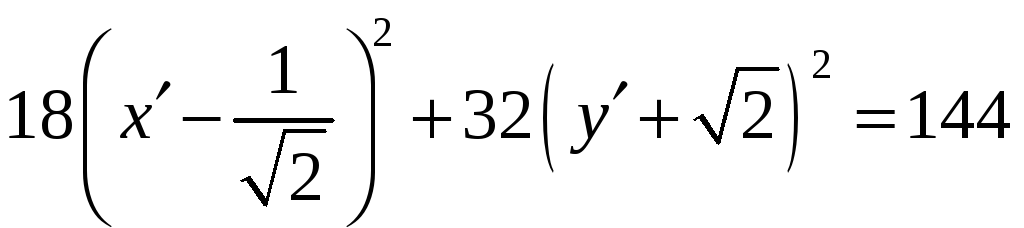
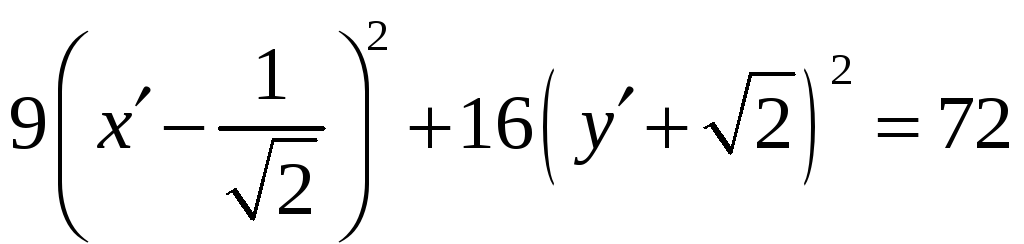
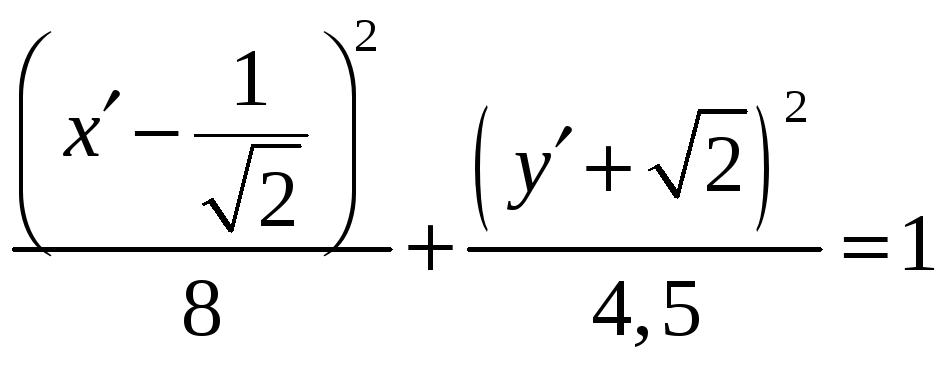
Это уравнение эллипса.

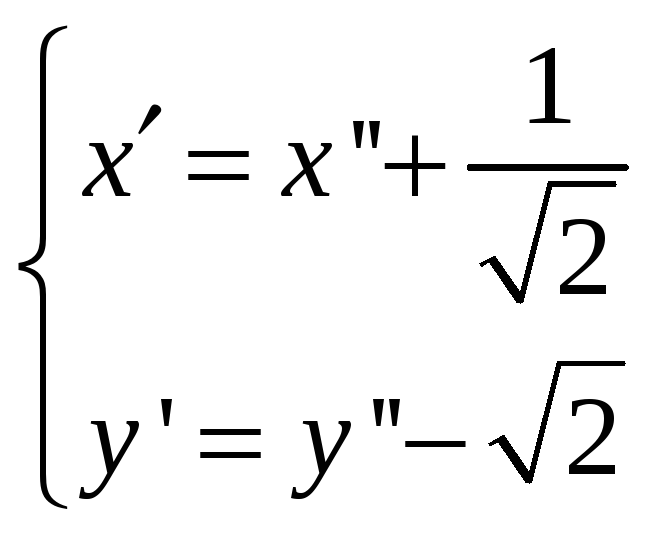
Эксцентриситет равен:

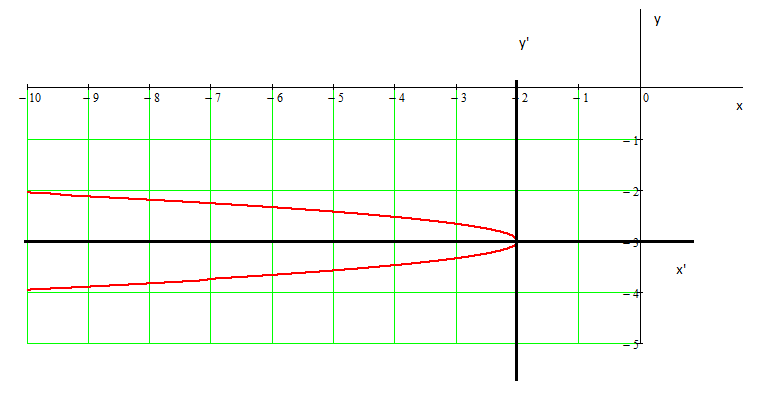
3. Определить, какую кривую второго порядка (или ее часть) задает уравнение, и изобразить ее на чертеже: .

Решение.

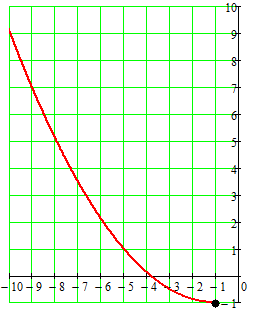
Это уравнение параболы.

Уравнение задает левую ветвь параболы.

1. Вычислить .

Решение.

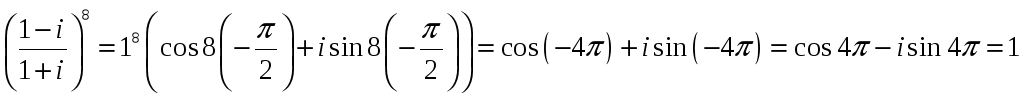
2. Извлечь корень .

Решение.

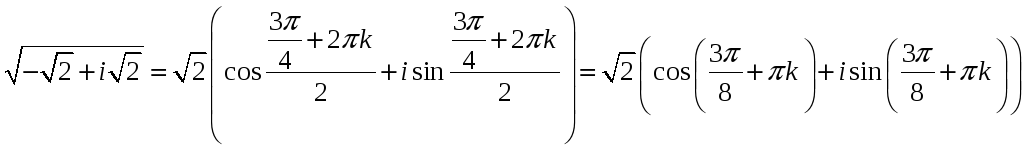
3. Решить уравнение

Решение.

Ответ: