19.2. Приближенное вычисление интеграла в приложениях Mathcad и Excel
Чтобы вычислить определенный интеграл в приложении Mathcad нужно записать интеграл, подынтегральную функцию и пределы интегрирования. Например:
Для получения численного значения записывается выражение:
z =
В приложении Excel можно составить программы по алгоритмам, приведенным выше, на языке VBA. Например, пусть на рабочем листе Excel в ячейках А1, А2, А3 располагаются значения a, b и n. Для вычисления интеграла по методу левых прямоугольников можно создать кнопку и составить неё следующую программу:
Sub CommandButton1_Click()
a = Range("A1")
b = Range("A2")
n = Range("A3")
h = (b - a) / n
For x = a To b - h Step h
S = S + Fp(x)
Next
z = S * h
Range("A4") = z
End Sub
Function Fp(x)
Fp = Sin(x) + 3
End Function
19.3. Численные методы решения уравнений
Пусть имеется уравнение: f(x) = 0.
Решение уравнения численными методами состоит из двух этапов:
отделение корней, т.е. нахождение таких отрезков [a,b] на оси OX, внутри которых имеется один корень;
вычисление корней с заданной точностью.
Одним из способов отделения корней является графический способ. Рассмотрим его на примере.
Пусть требуется отделить корни уравнения 3 – x – ln(x) = 0.
y
= 3 – x Рис.
19.3. Графики функций
1.
С помощью микрокалькулятора вычислить
приближенно значение определенного
интеграла из табл.1 для n=4.
Номер варианта определяет преподаватель.
Для нечетных по номеру вариантов
использовать метод трапеций, для четных
– метод парабол.
2.
Написать программу, реализующую
вычисление определённого интеграла
соответствующим методом. Для всех
вариантов принять n=20.
3.
Выполнить вычисления в пакете MathCAD.
Результаты сравнить между собой. Таблица 1
Номер вар. Функция Пределы
интегри-рования Номер
вар. Функция Пределы
интегри-рования 1 x3+x-3 a=1,
b=2 9 x3+3x-1 a=4,
b=8 2 ln(x)+x+3 a=3,
b=4 10 x3+x-1 a=3,
b=4 3 x3+2x-11 a=6,
b=7 11 ln(x)+x3 a=3,
b=7 4 2ln(x)-1/x a=8,
b=9 12 ex-2x2-1 a=2,
b=9 5 2-x2+x a=1,
b=3 13 2x+ln(x)+7 a=2,
b=4 6 5x-1+x3 a=2,
b=5 14 x3+2x-4 a=1,
b=5 7 1+ex+x a=3,
b=8 15 2-x+ln(x) a=3,
b=7 8 x3+x-2 a=6,
b=9 16 x2+4x+2 a=6,
b=8
апеций y
= ln(x)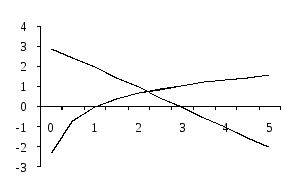
П
Приближенное решение уравнений
Можно также отделить корни, построив график функции f(x) в приложении Mathcad или в приложении Excel.
После того, как определен отрезок (или отрезки), внутри которого имеется один корень, можно вычислить его с заданной точностью одним из методов.
Метод касательных. При использовании данного метода для вычисления корня уравнения необходимо определить начальное приближение корня x0: x0 = a, если знаки f(a) и f(a) совпадают, и x0 = b, если знаки f(b) и f(b) совпадают. Последовательные приближения корня рассчитываются по формуле
xn+1
= xn
–
,n
= 0, 1 ,2, ….
Вычисления продолжаются до тех пор, пока не будет выполнено условие xn+1 – xn <= e, где e – требуемая точность вычисления корня.
Рассмотрим алгоритм метода касательных:
1. Ввод значений a, b, e.
2. Вычисление начального приближения корня xn1 = a, если
f(a) f(a) > 0 или xn1 = b в противном случае.
3. Вычисление xn = xn1.
4. Определение очередного приближения корня по формуле
xn1
= xn
–
5. Если xn1 – xn > e, то переход к пункту 3, в противном случае – переход к п. 6.
6. Вывод значения корня xn1.
Метод дихотомии (деления отрезка пополам). При использовании метода дихотомии отрезок [a, b] делится пополам. Из полученных двух отрезков для дальнейших вычислений выбирается тот, на концах которого функция f(x) имеет разные знаки. Выбранный отрезок вновь делится пополам. Вычисления продолжаются до тех пор, пока величина последнего из полученных отрезков не станет меньше 2e.
Рассмотрим алгоритм метода дихотомии:
1. Ввод значений a, b, e.
2.
Вычисление
.
3. Если f(x) = 0, то переход к п. 6, иначе – переход к п. 4.
4. Если f(x)f(a) <= 0, то b = x, иначе – a = x.
5. Если a – b > 2e, то переход к п. 2, иначе – переход к следующему пункту.
6. Вывод значения корня x.