
Лабораторная работа 3 функциональные последовательности
1.Найти
предельную функцию
![]() для последовательности
для последовательности
![]() на
на
![]()
1.1
![]() ,
,
![]() ;
;
1.2
![]() ,
,
![]() ;
;
1.3
![]()
![]() ;
;
1.4
![]() ,
,![]() ;
;
1.5
![]() ,
,
![]() ;
;
1.6
![]() ,
,
![]() ;
;
1.7
![]() ,
,![]() ;
;
1.8
![]() ,
,![]() ;
;
1.9
![]() ,
,
![]() ;
;
1.10
![]() ,
,![]() ;
;
1.11
![]() ,
,![]() ;
;
1.12
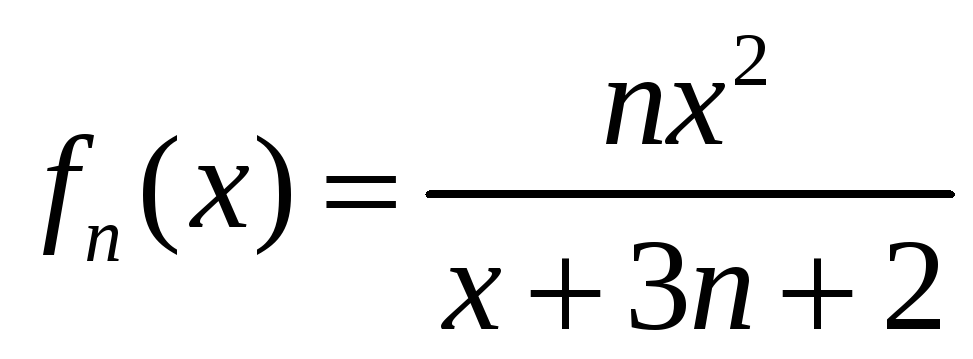 ,
,
![]() .
.
2.
Исследовать сходимость и равномерную
сходимость
![]() на множестве
на множестве![]()
2.1 а)
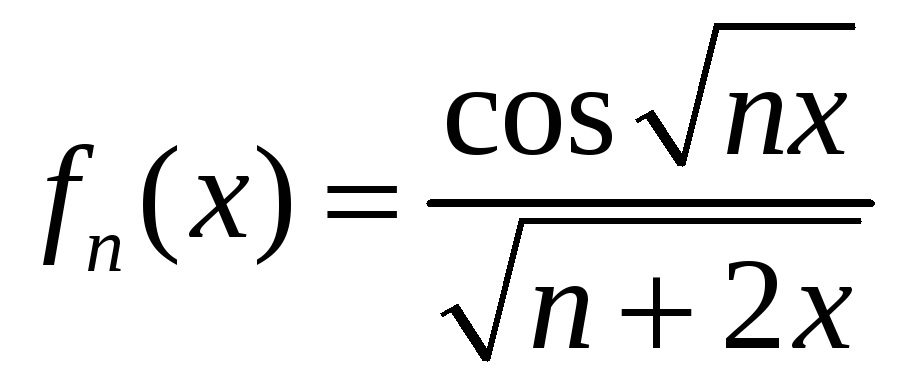 ,
,![]() ; б)
; б)
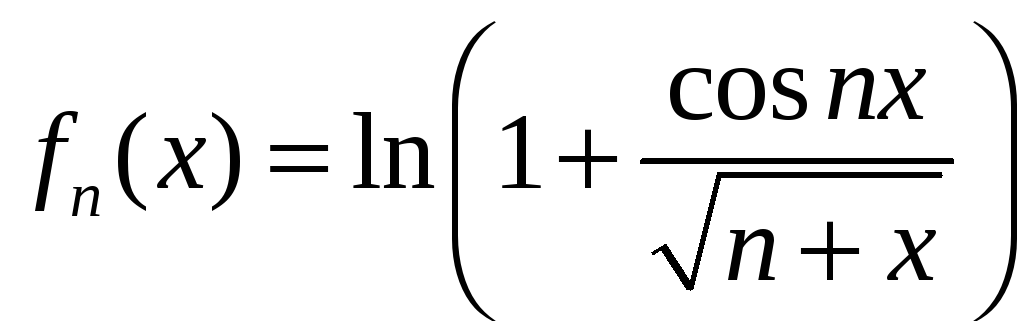 ,
,![]() ;
;
2.2
а)
![]() ,
,![]() ; б)
; б)
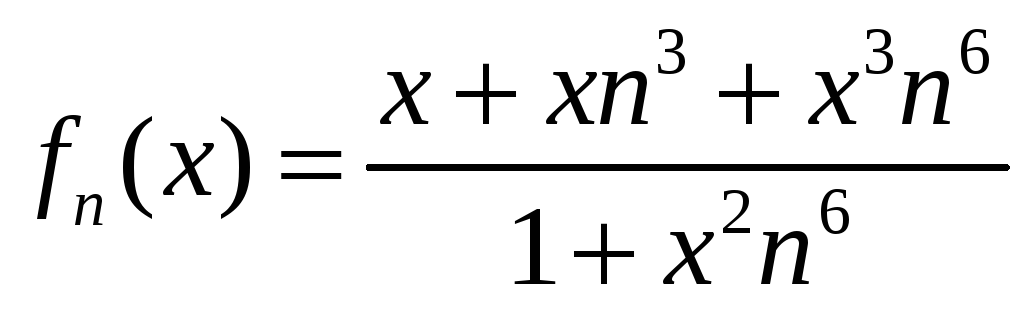 ,
,![]() ;
;
2.3
а)
![]()
![]() ; б)
; б)![]() ,
,![]() ;
;
2.4
а)
![]() ,
,
![]() ; б)
; б)
![]() ,
,
![]() ;
;
2.5
а)
![]() ,
,![]() ; б)
; б)
![]()
![]() ;
;
2.6
а)
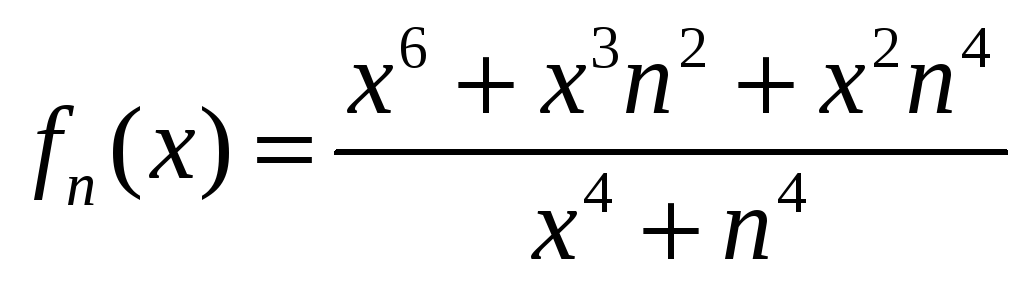 ,
,![]() ; б)
; б)
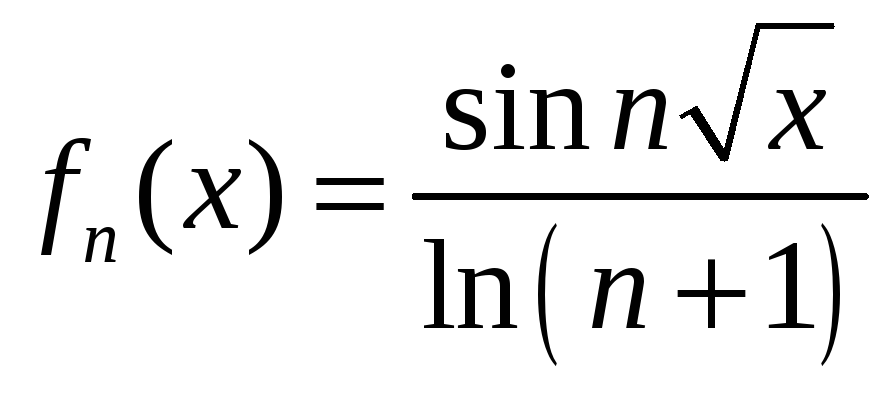
![]() ;
;
2.7 а)
![]()
![]() ; б)
; б)
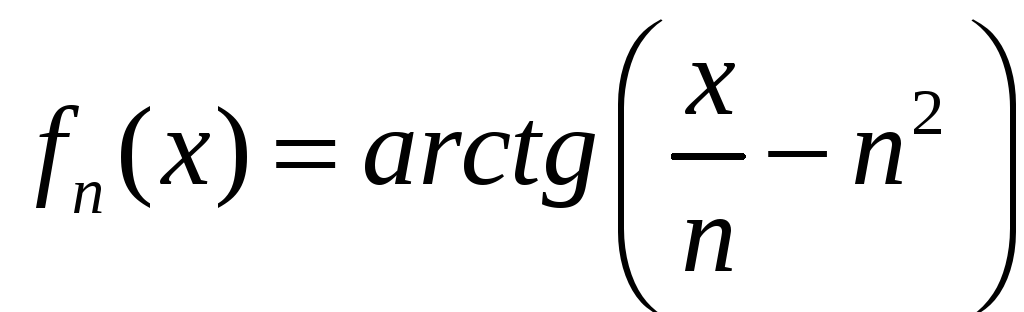 ,
,![]() ;
;
2.8 а)
![]() ,
,![]() ; б)
; б)
![]() ,
,![]() ;
;
2.9 а)
![]() ,
,![]() ; б)
; б)
![]()
![]() ;
;
2.10 а)
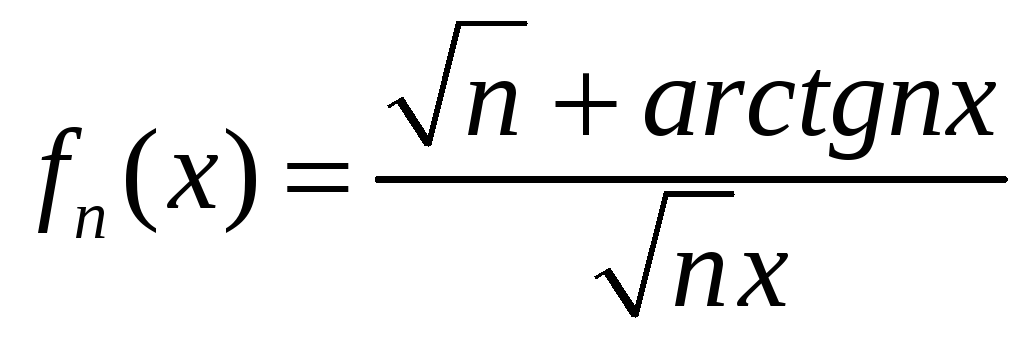 ,
,![]() ; б)
; б)
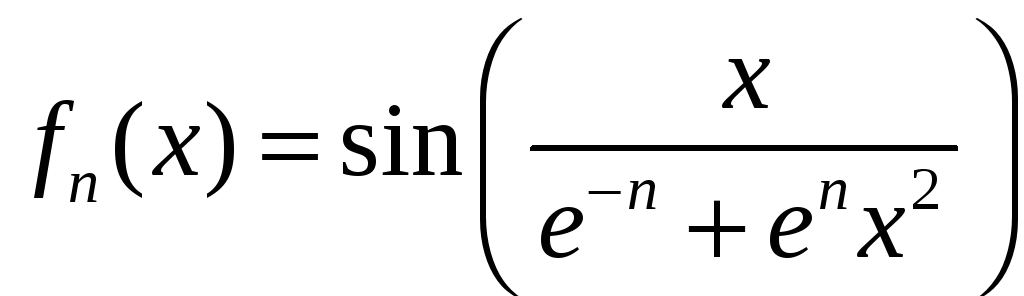 ,
,![]() ;
;
2.11 а)
![]() ,
,![]() ; б)
; б)
![]() ,
,![]() ;
;
2.12 а)
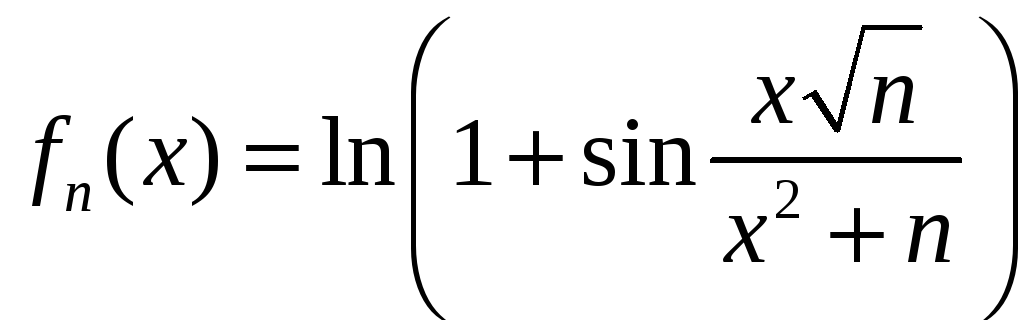 ,
,![]() ; б)
; б)
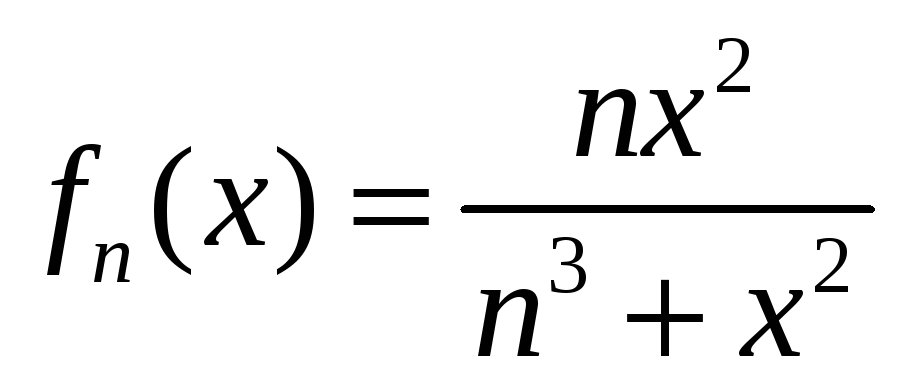
![]() .
.
3.Доказать:
3.1
Если последовательности
![]() и
и
![]() равномерно сходятся на множестве
равномерно сходятся на множестве![]() ,
то
,
то
![]() последовательность
последовательность
![]() равномерно сходится на множестве
равномерно сходится на множестве![]() .
.
3.2
Если последовательность
![]() равномерно сходится на множестве
равномерно сходится на множестве![]() и
функция
и
функция
![]() ограничена на
ограничена на![]() ,
то последовательность
,
то последовательность
![]() равномерно сходится на этом множестве.
равномерно сходится на этом множестве.
3.3
Если
![]() -
произвольная функция на
-
произвольная функция на
![]() ,
то последовательность
,
то последовательность
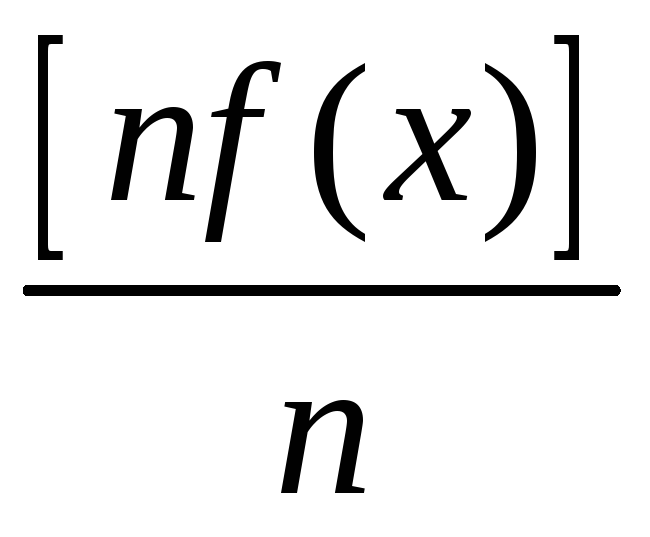 сходится равномерно к
сходится равномерно к
![]() на
на
![]() .
.
3.4
Если
![]() имеет непрерывную производную на
имеет непрерывную производную на
![]() ,
то последовательность
,
то последовательность
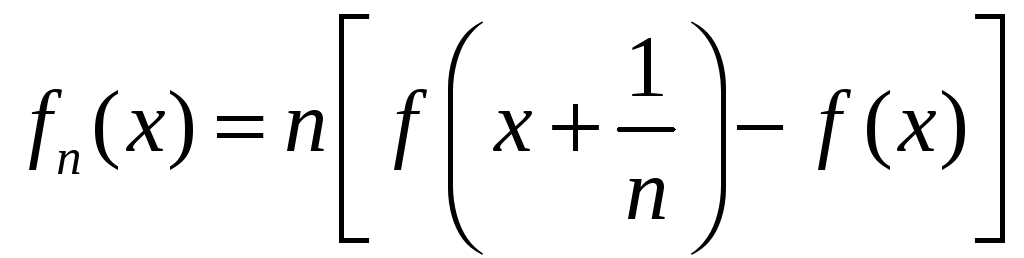 сходится равномерно к
сходится равномерно к
![]() на
на
![]() ,
где
,
где
![]() .
.
3.5
Если последовательность многочленов
степени не выше
![]() равномерно сходится на
равномерно сходится на
![]() ,
то предельная функция этой последовательности
– многочлен степени не выше
,
то предельная функция этой последовательности
– многочлен степени не выше
![]() .
.
3.6

3.8
Если последовательности
![]() и
и
![]() поточечно сходятся на множестве
поточечно сходятся на множестве
![]() ,
то
,
то
![]() последовательность
последовательность
![]() поточечно сходится на множестве
поточечно сходится на множестве![]()
3.9
Если последовательности
![]() и
и
![]() поточечно сходятся на множестве
поточечно сходятся на множестве
![]() ,
то последовательность
,
то последовательность
![]() поточечно сходится на множестве
поточечно сходится на множестве![]() .
.
3.10 Если
последовательность
![]() равномерно сходится на множестве
равномерно сходится на множестве![]() и
функция
и
функция
![]() равномерно непрерывна на
равномерно непрерывна на![]() при
каждом
при
каждом
![]() ,
то функция
,
то функция
![]() равномерно непрерывна на этом множестве.
равномерно непрерывна на этом множестве.
Лабораторная работа 4 функциональные ряды
1.Найти область сходимости и абсолютной сходимости ряда:
1.1
а)
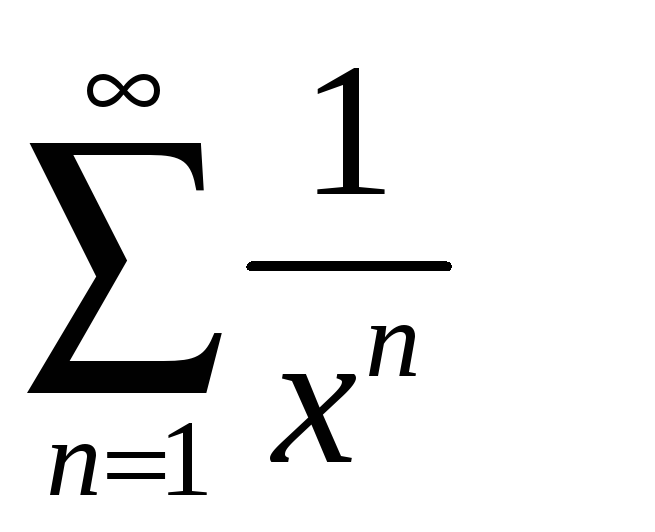 ;
б)
;
б)
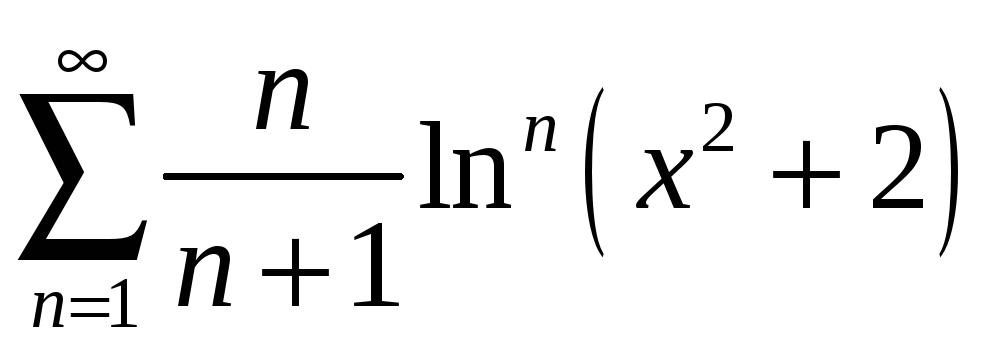 ;
;
1.2
а)
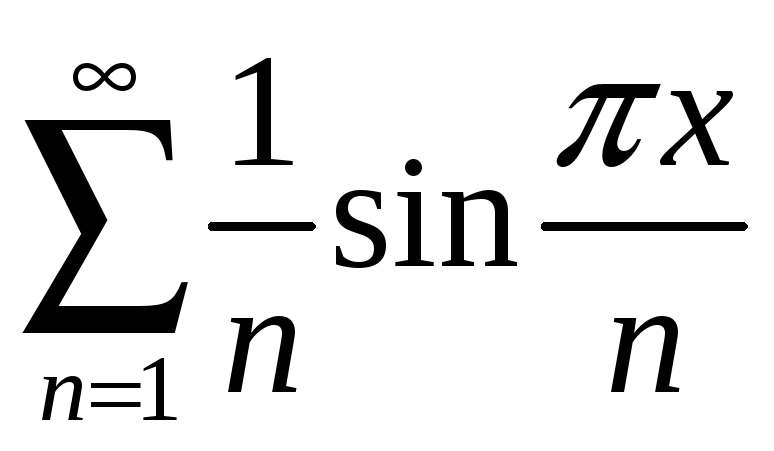 ;
б)
;
б)
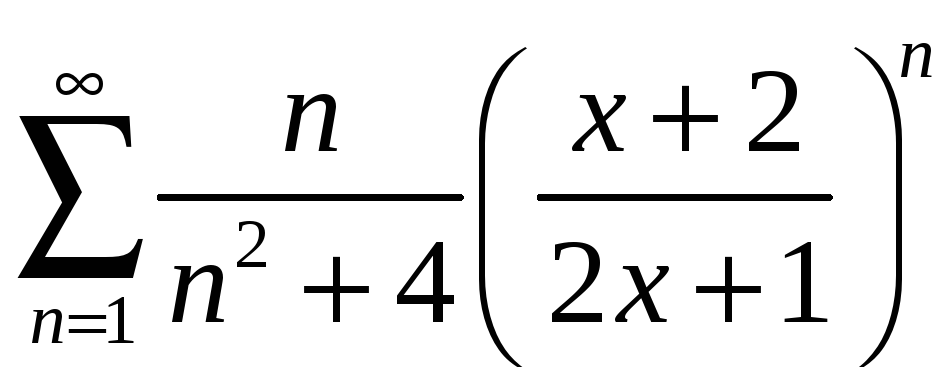 ;
;
1.3
а)
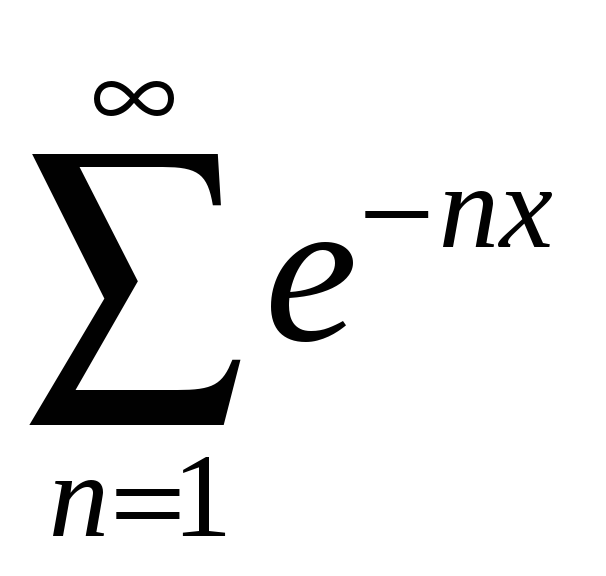 ;
б)
;
б)
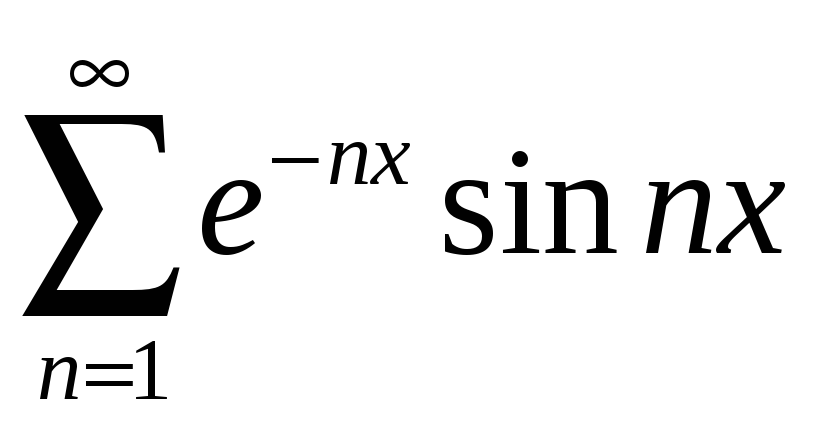 ;
;
1.4
а)
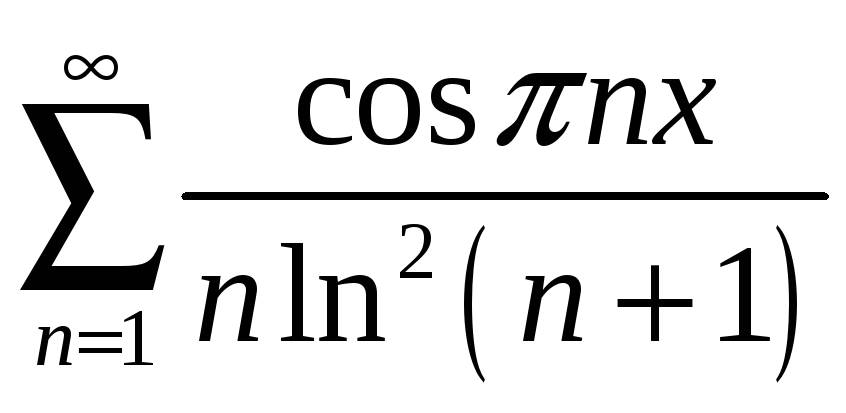 ;
б)
;
б)
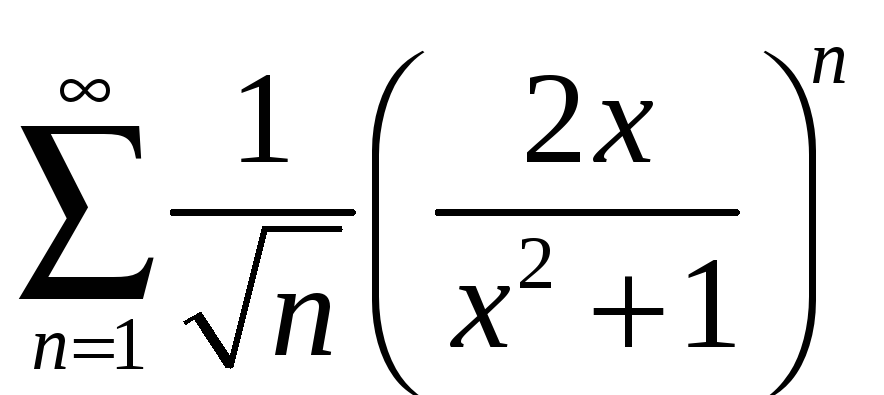 ;
;
1.5
а)
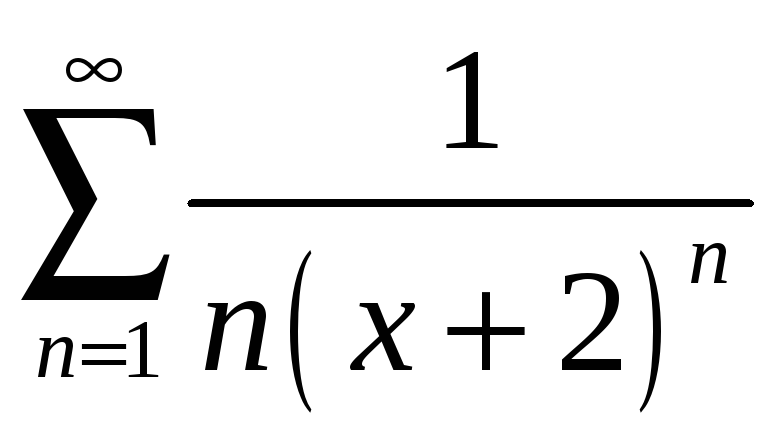 ;
б)
;
б)
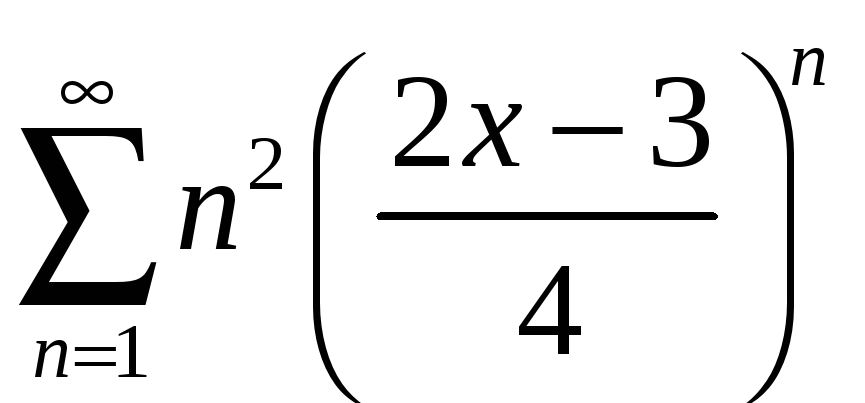 ;
;
1.6
а)
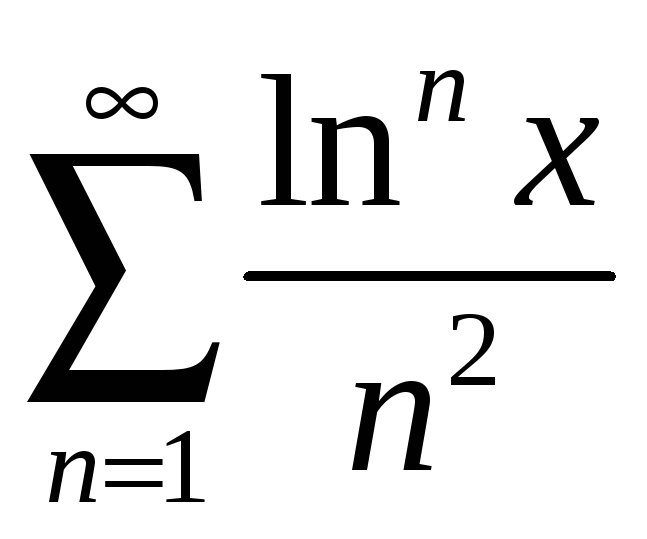 ;
б)
;
б)
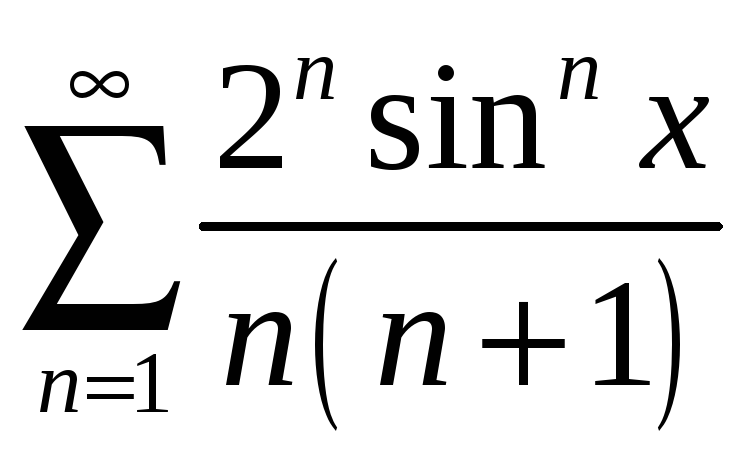 ;
;
1.7
а)
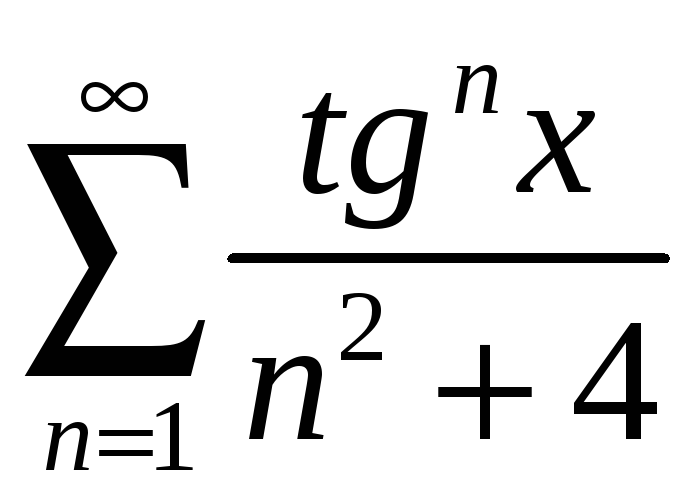 ;
б)
;
б)
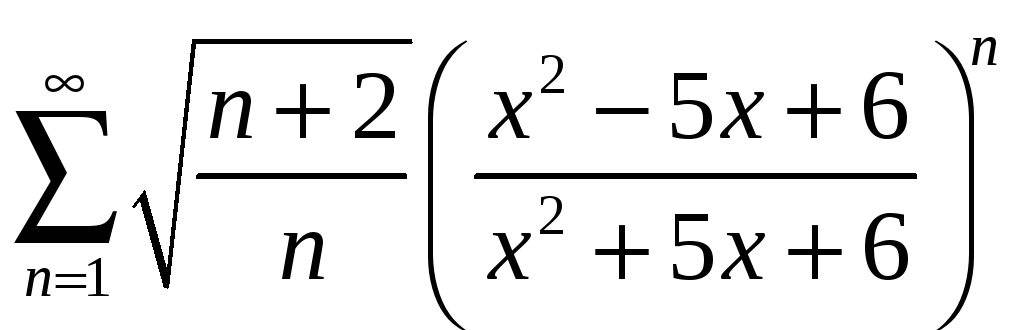 ;
;
1.8
а)
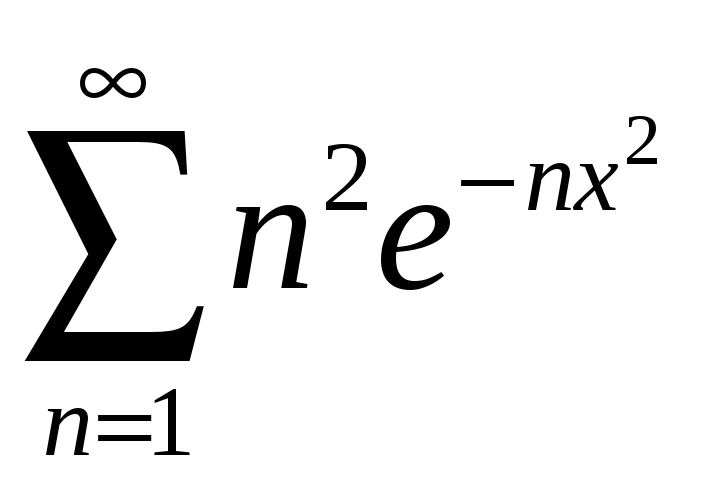 ;
б)
;
б)
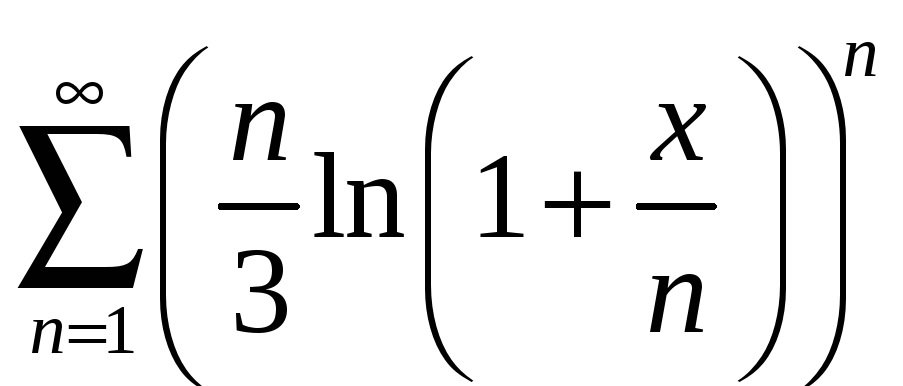 ;
;
1.9
а)
![]() ;
б)
;
б)
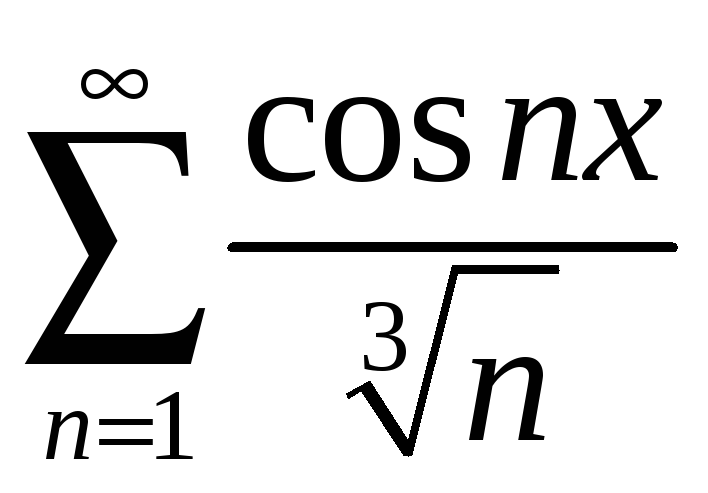 ;
;
1.10
а)
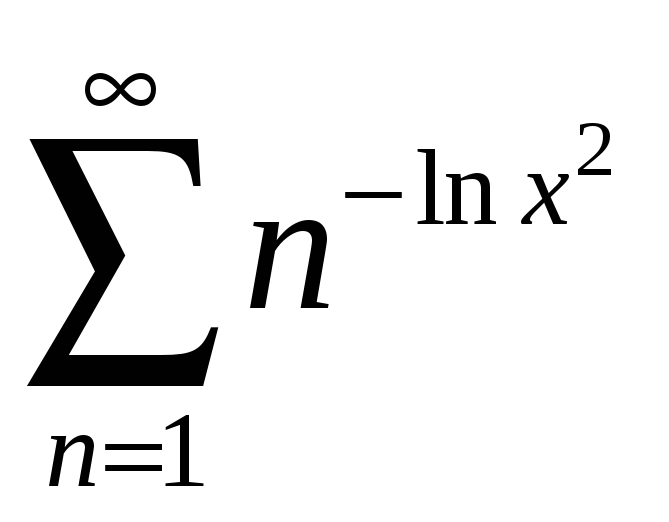 ;
б)
;
б)
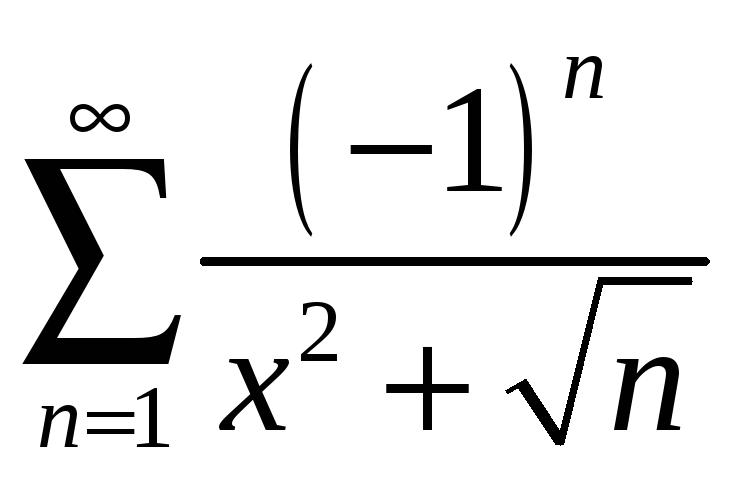 ;
;
1.11 а)
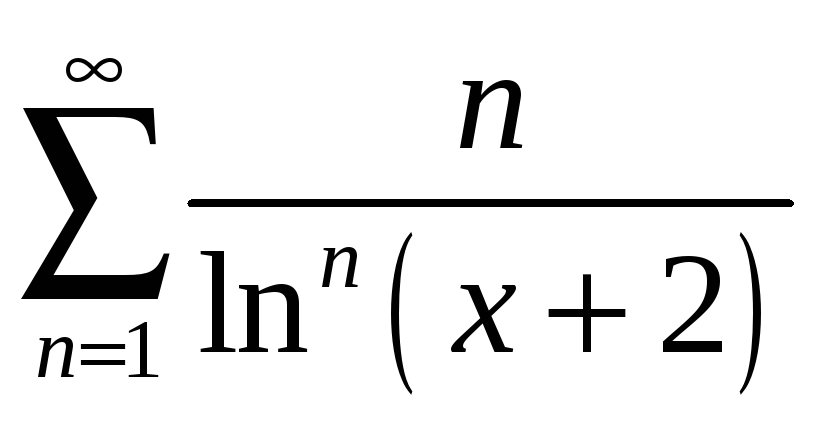 ;
б)
;
б)
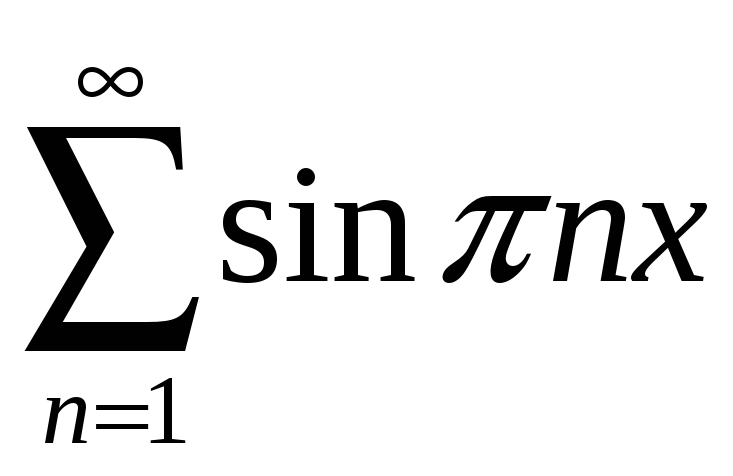 ;
;
1.12
а)
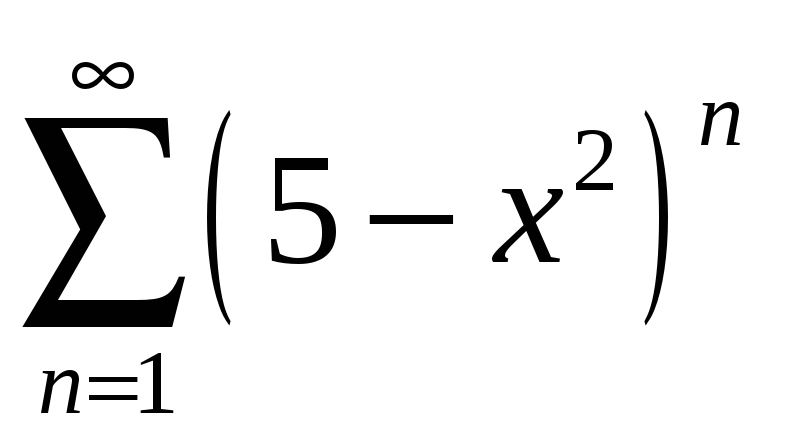 ;
б)
;
б)
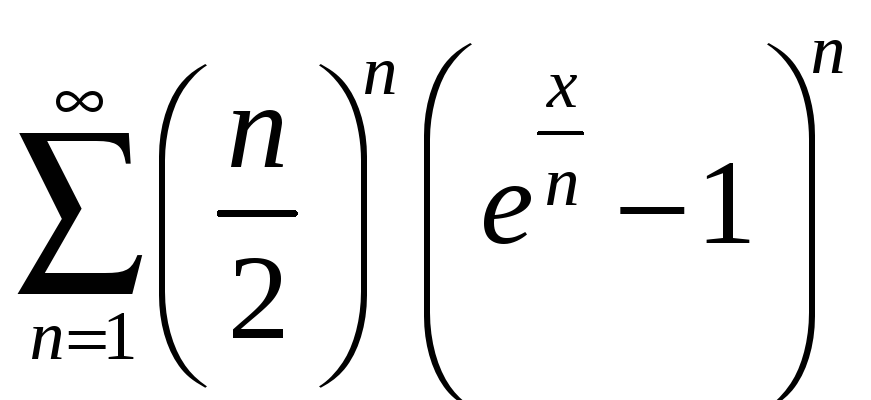 .
.
2.Исходя из определения равномерной сходимости, доказать равномерную сходимость ряда на указанном промежутке
2.1
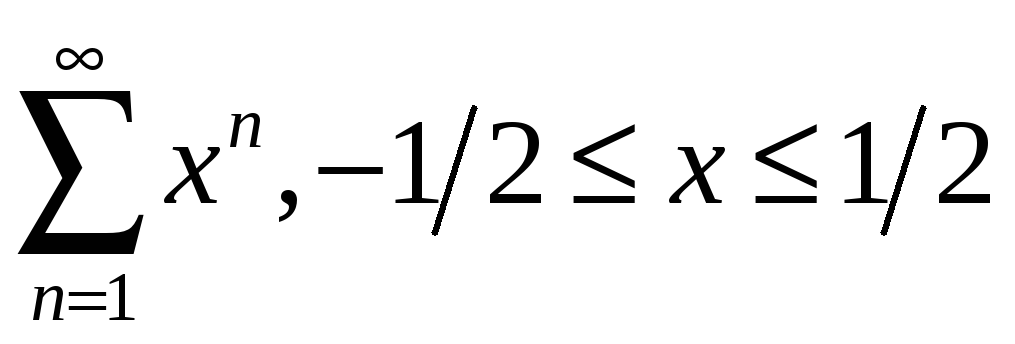 ;
2.6
;
2.6
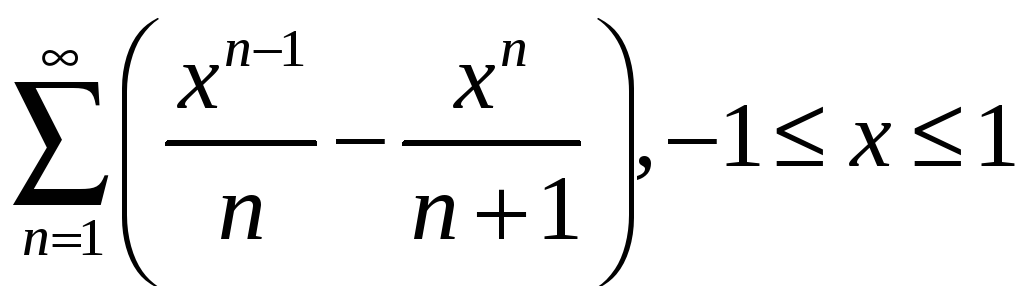 ;
;
2.2
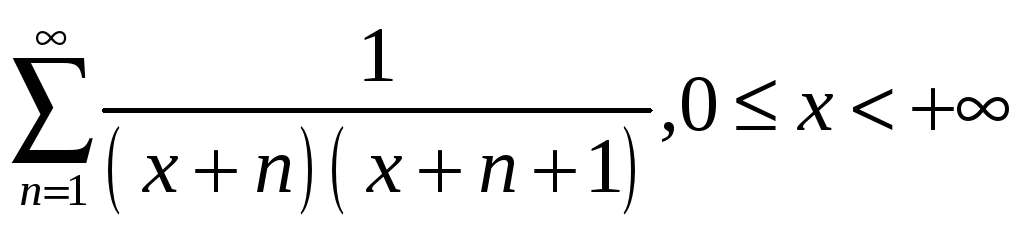 ;
2.7
;
2.7
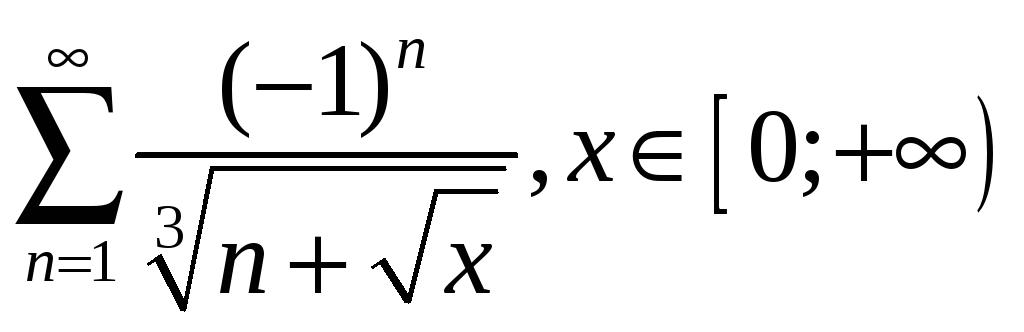 ;
;
2.3
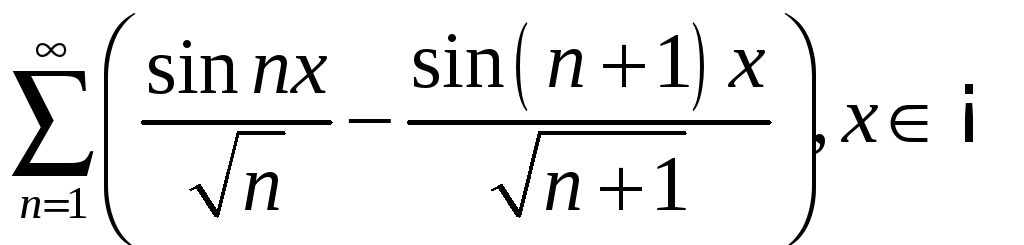 ;
2.8
;
2.8
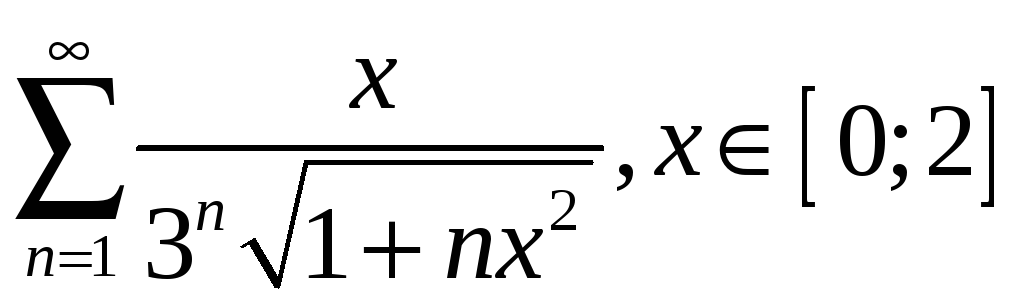 ;
;
2.4
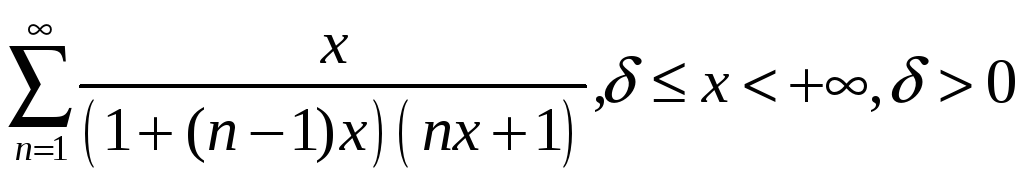 ;
2.9
;
2.9
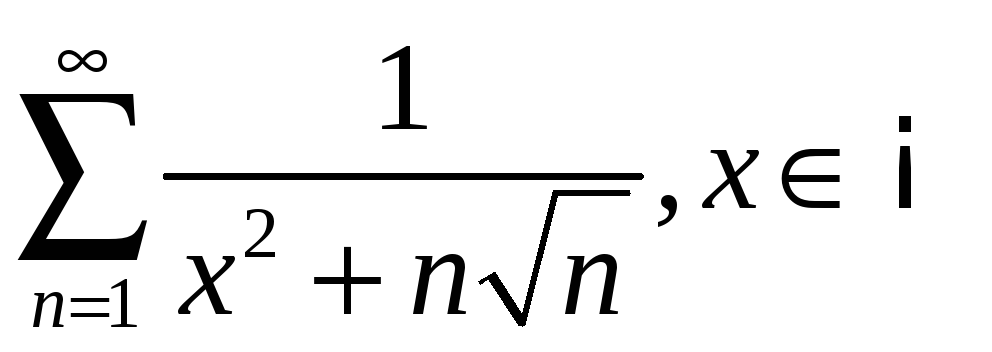 ;
;
2.5
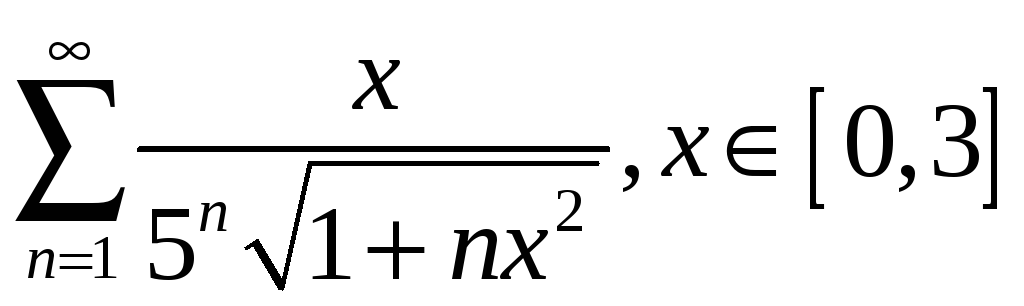 ;
2.10
;
2.10
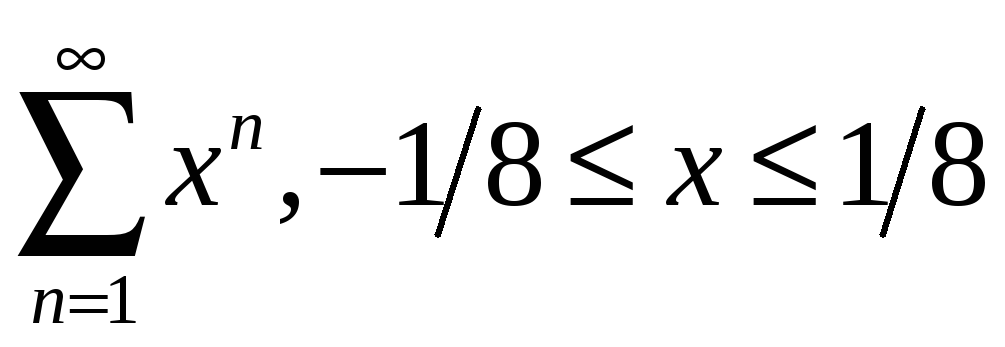 .
.
3 Пользуясь признаком Вейерштрасса, доказать равномерную сходимость ряда.
3.1
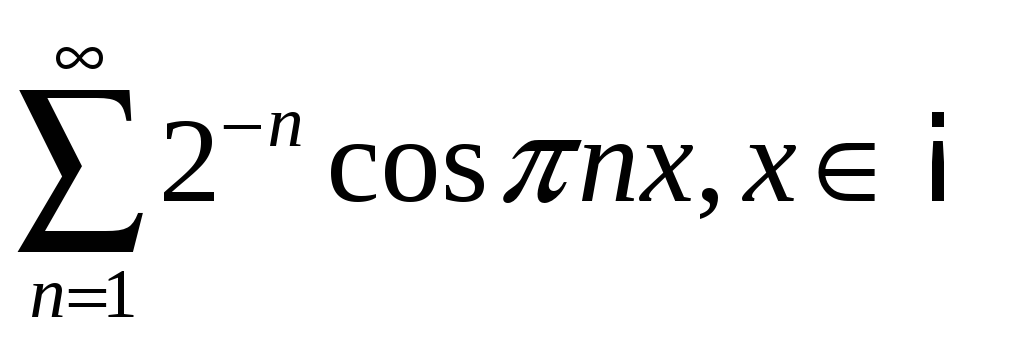 ;
3.7
;
3.7
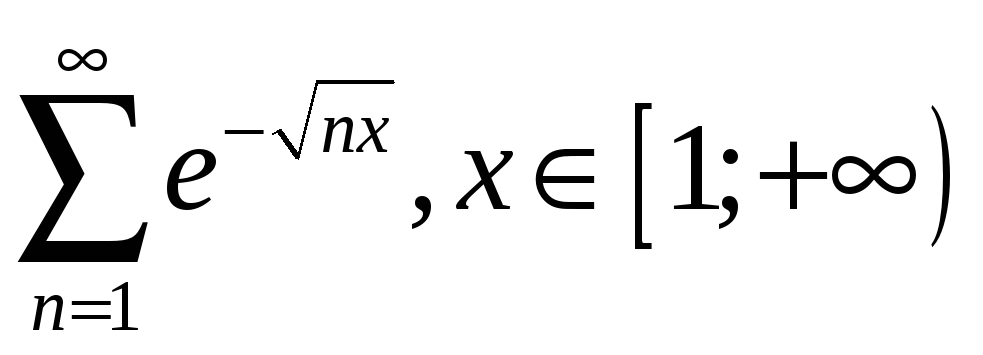 ;
;
3.2
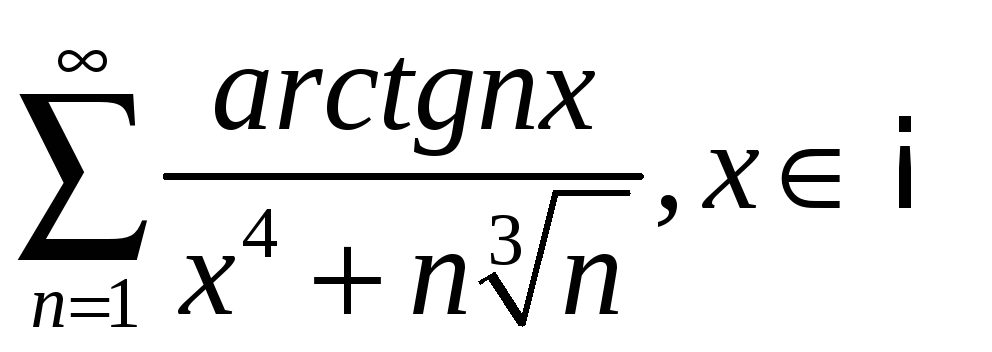 ;
3.8
;
3.8
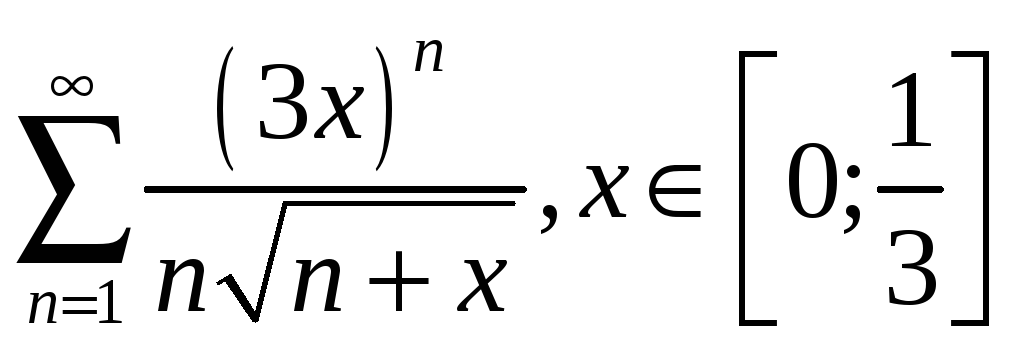 ;
;
3.3
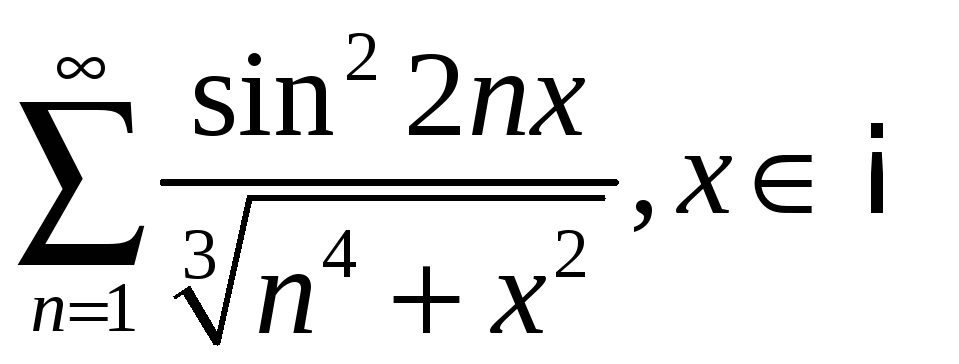 ;
3.9
;
3.9
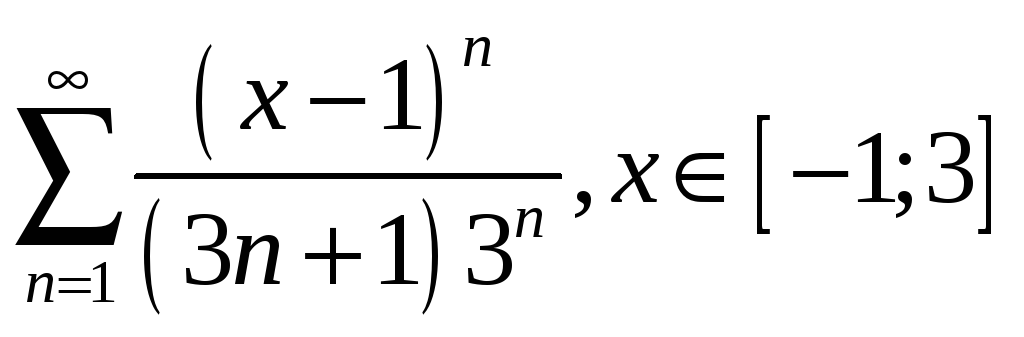 ;
;
3.4
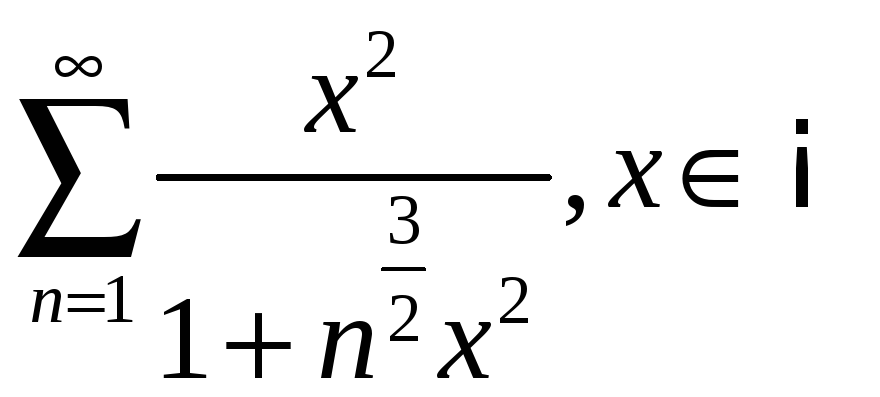 ;
3.10
;
3.10
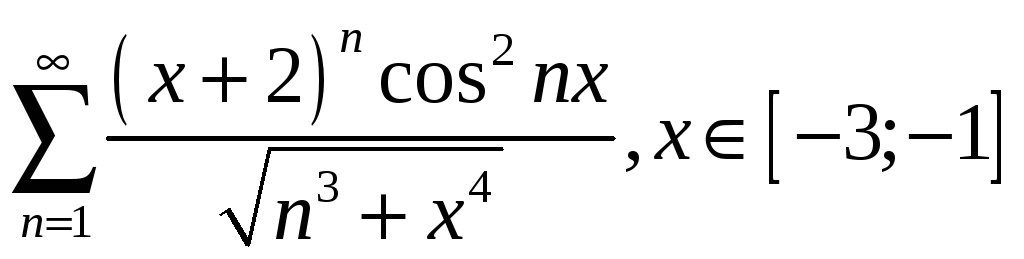 ;
;
3.5
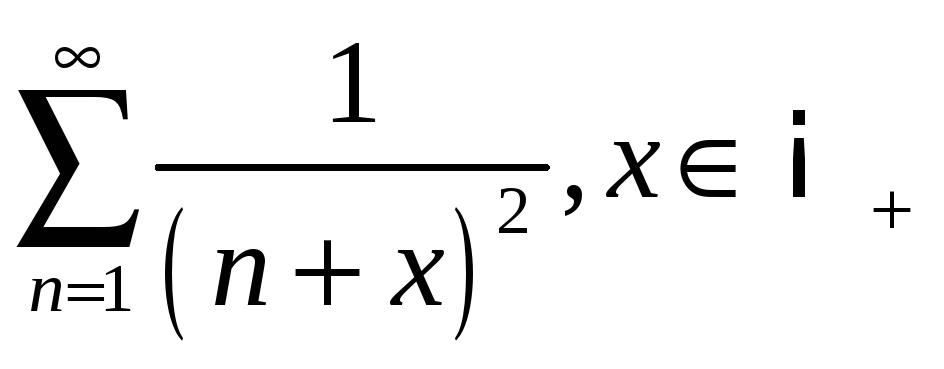 ;
3.11
;
3.11
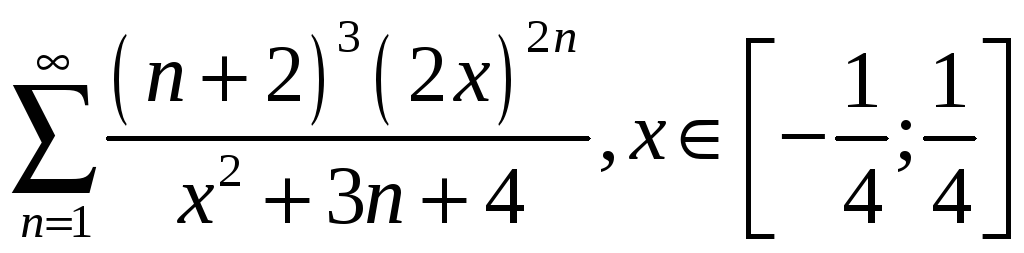
3.6
 ;
3.12
;
3.12
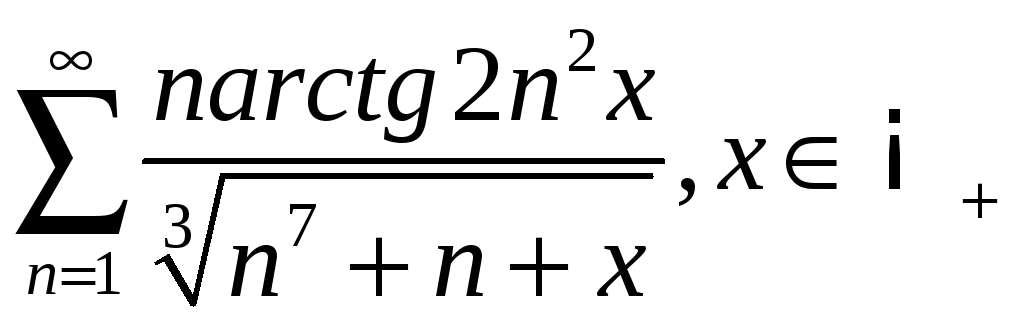 .
.
4.Исследовать сходимость и равномерную сходимость ряда.
4.1
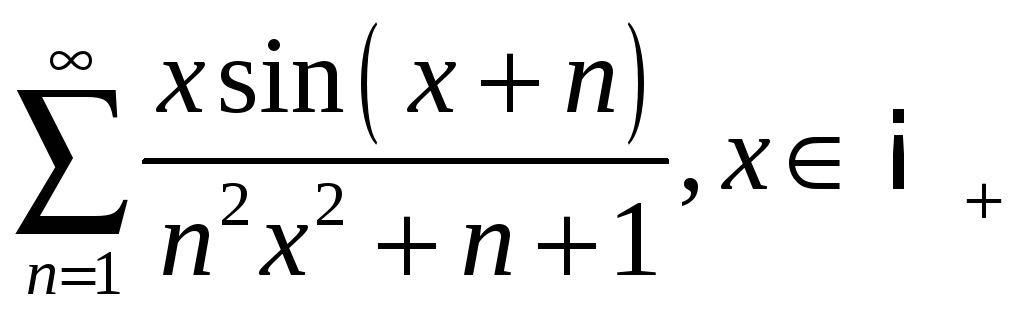 ;
4.6
;
4.6
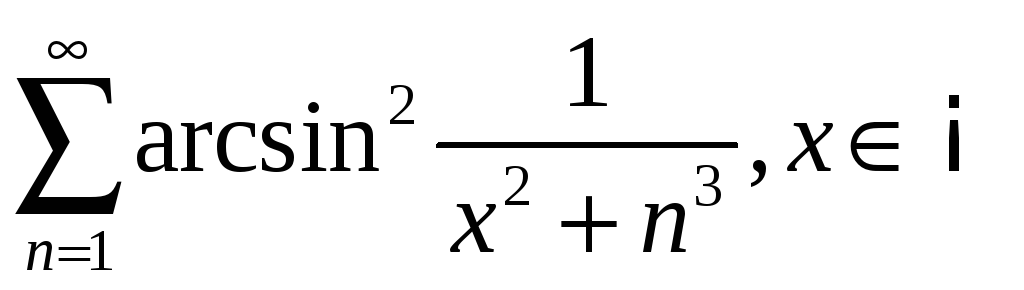 ;
;
4.2
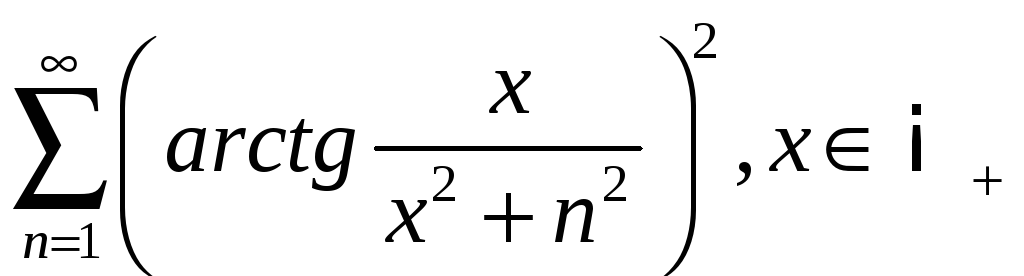 ;
4.7
;
4.7
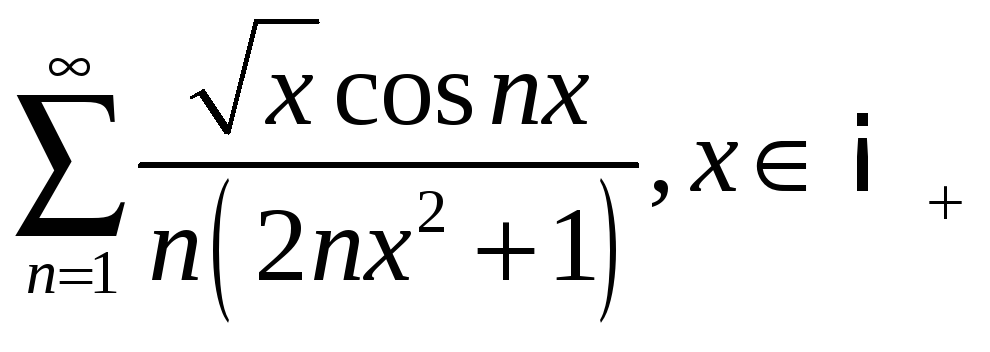 ;
;
4.3
![]() ;
4.8
;
4.8
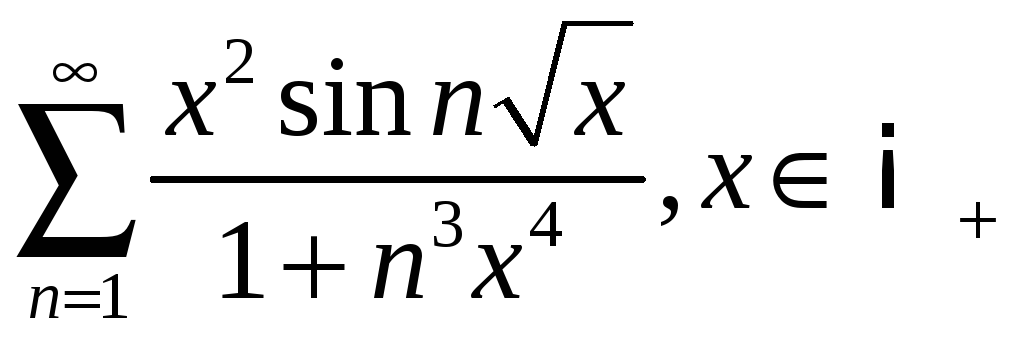 ;
;
4.4
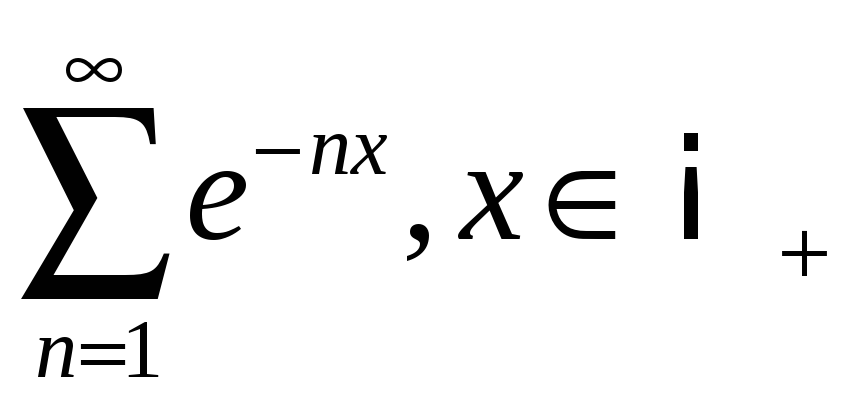 ;
4.9
;
4.9
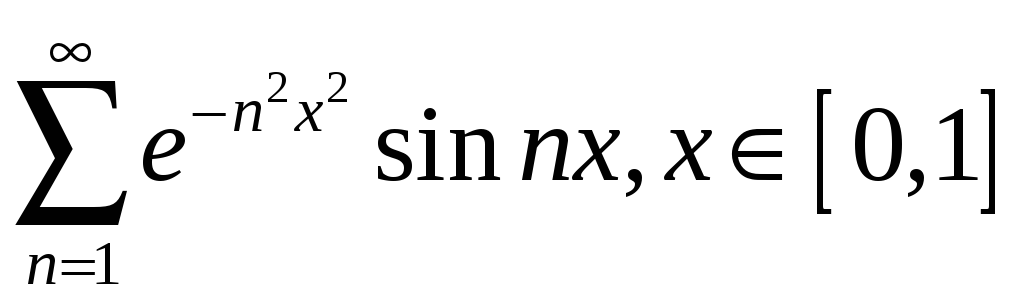 ;
;
4.5
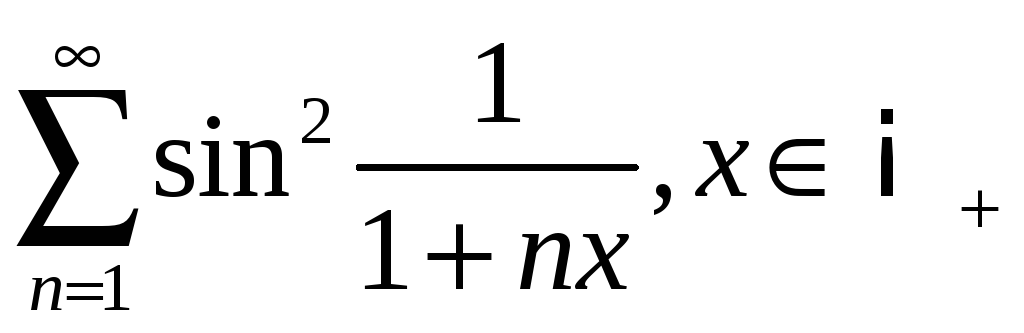 ;
4.10
;
4.10
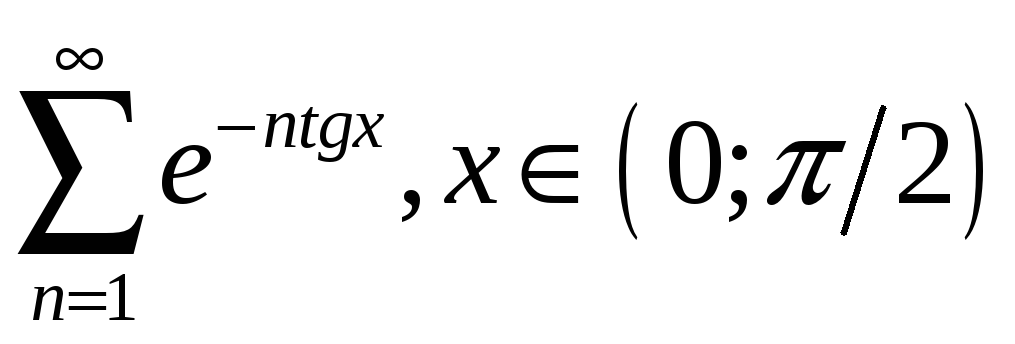 .
.
