
Лабораторная работа 1 ряды с неотрицательными членами
1 Исследовать сходимость ряда с помощью признака сравнения
1.1
a)
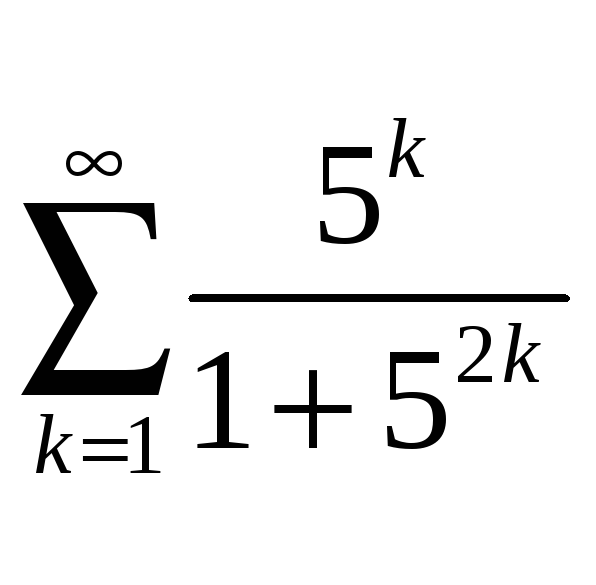 ; б)
; б)
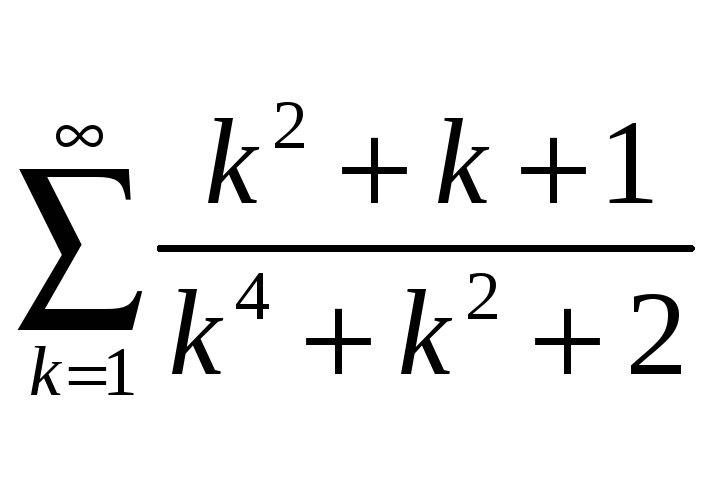 ;
;
1.2
а)
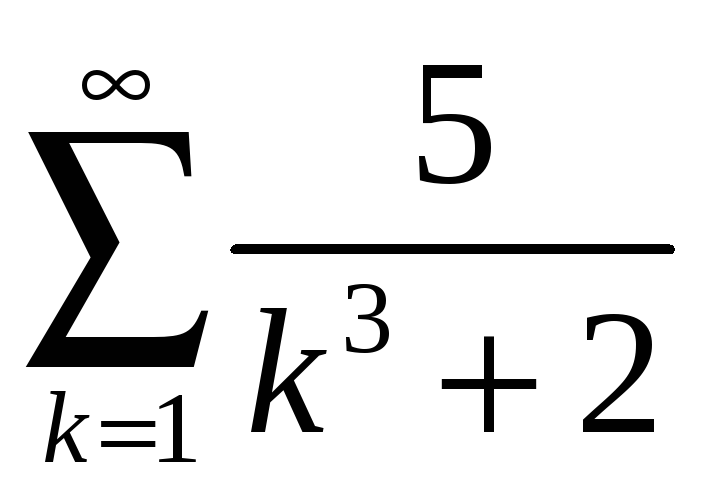 ; б)
; б)
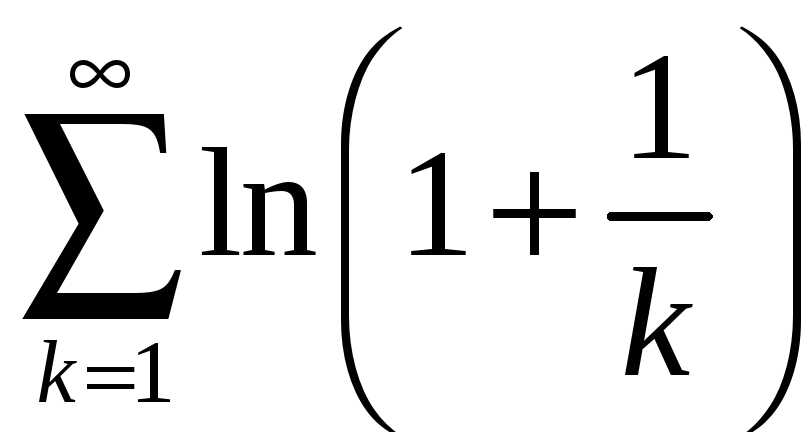 ;
;
1.3
а)
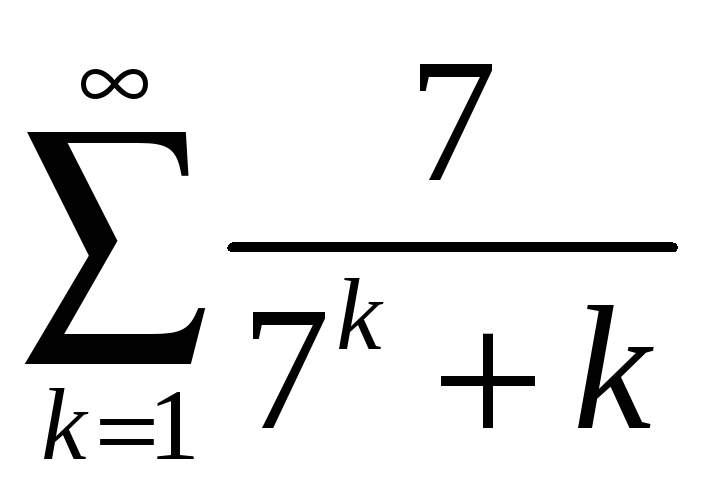 ; б)
; б)
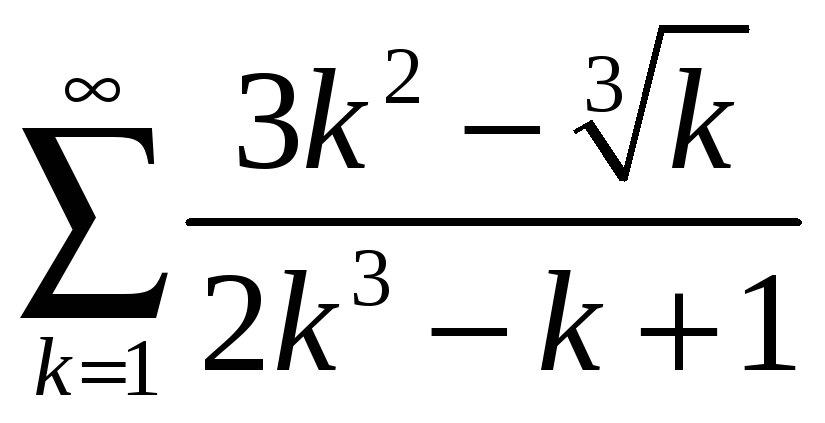 ;
;
1.4
а)
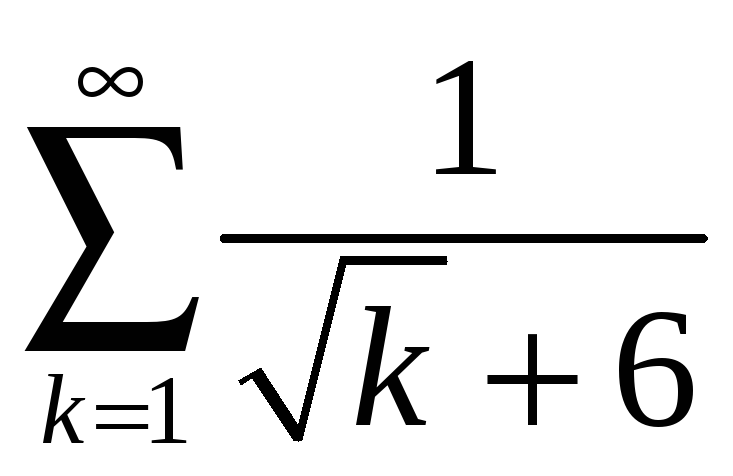 ; б)
; б)
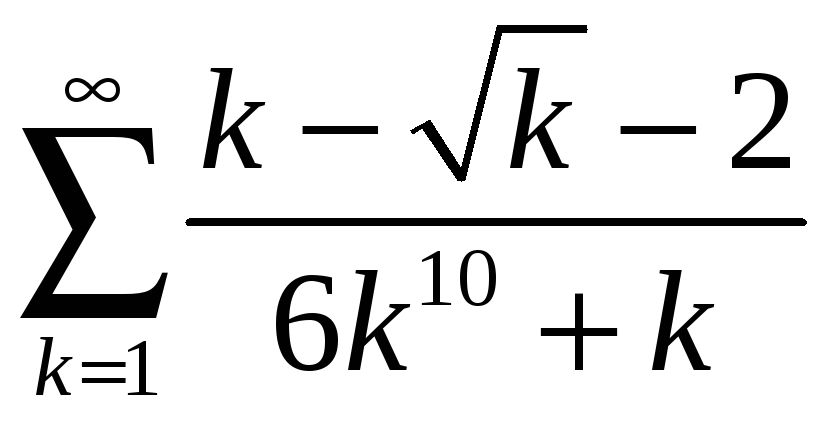 ;
;
1.5
а)
![]() ; б)
; б)
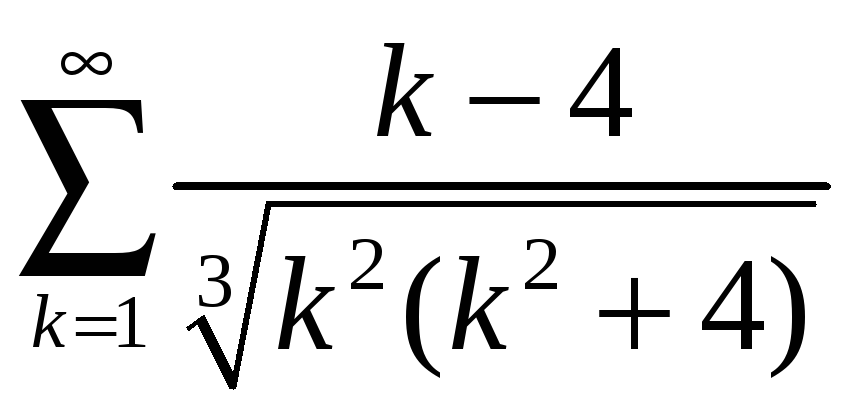 ;
;
1.6
а)
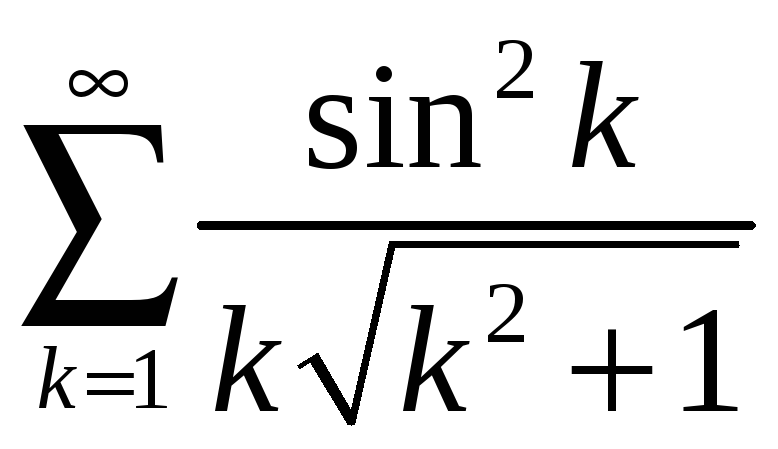 ; б)
; б)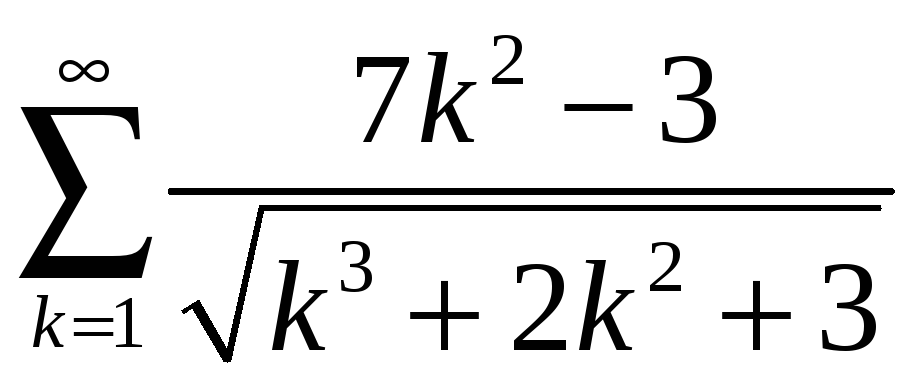 ;
;
1.7
а)
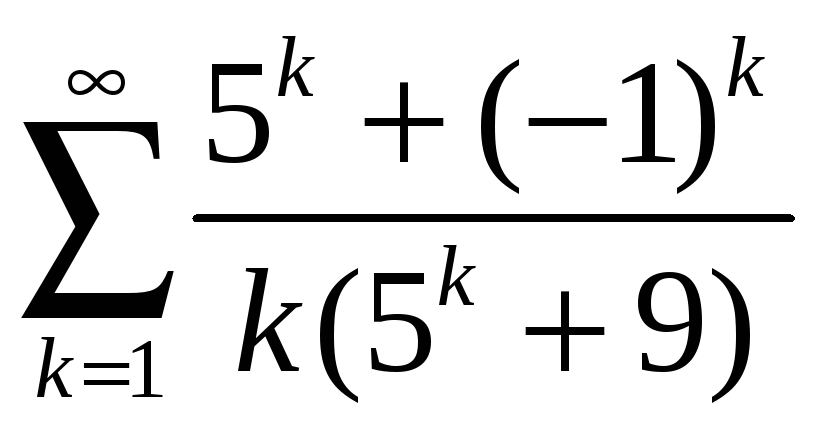 ; б)
; б)
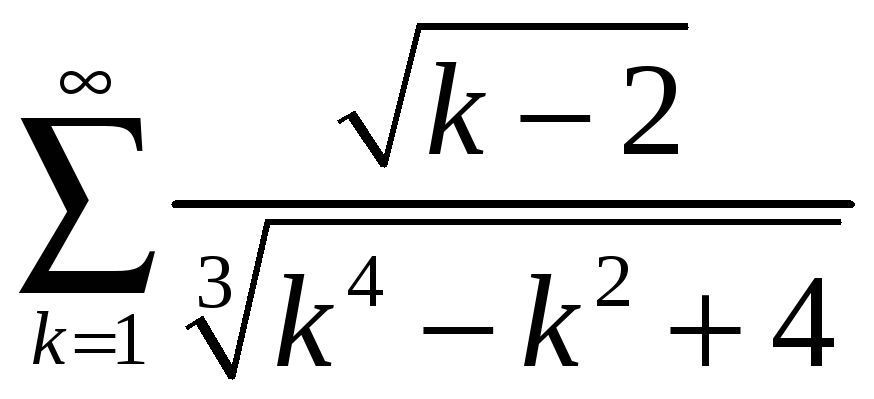 ;
;
1.8
a)
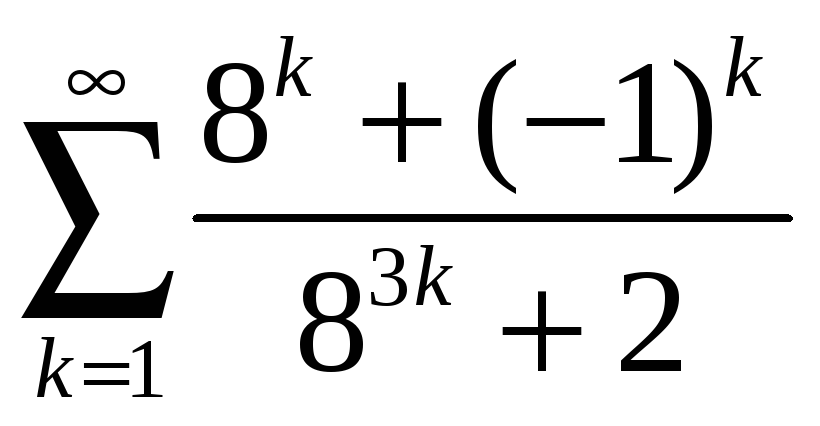 ; б)
; б)
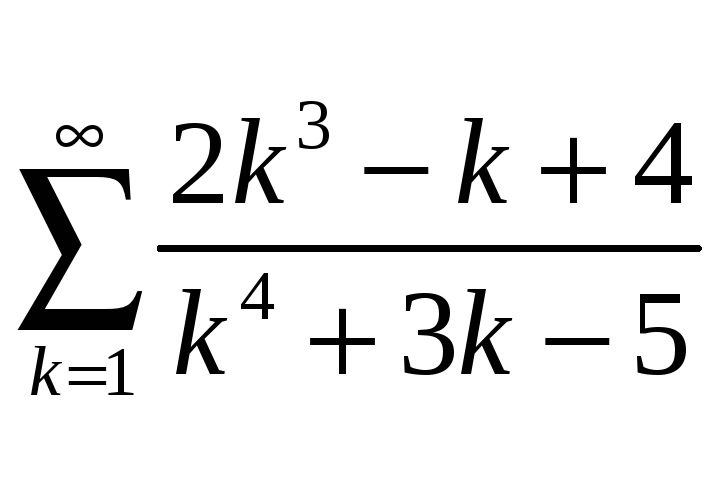 ;
;
1.9
а)
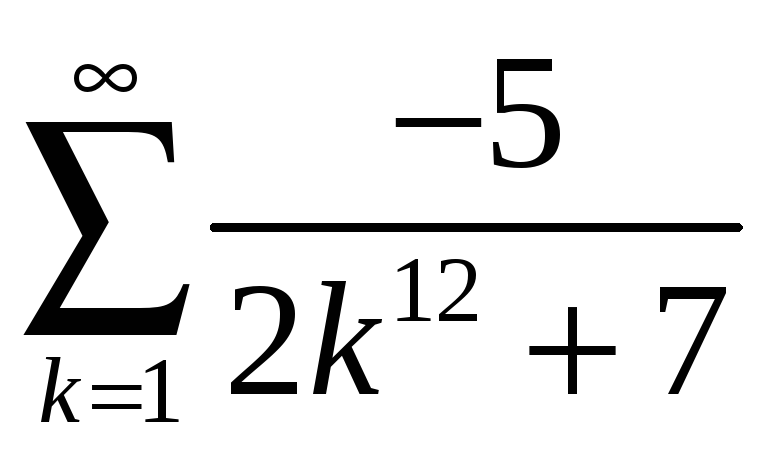 ; б)
; б)
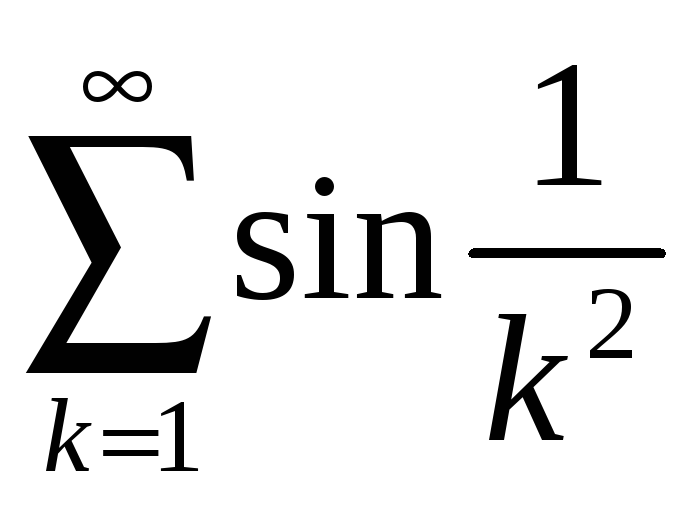 ;
;
1.10
а)
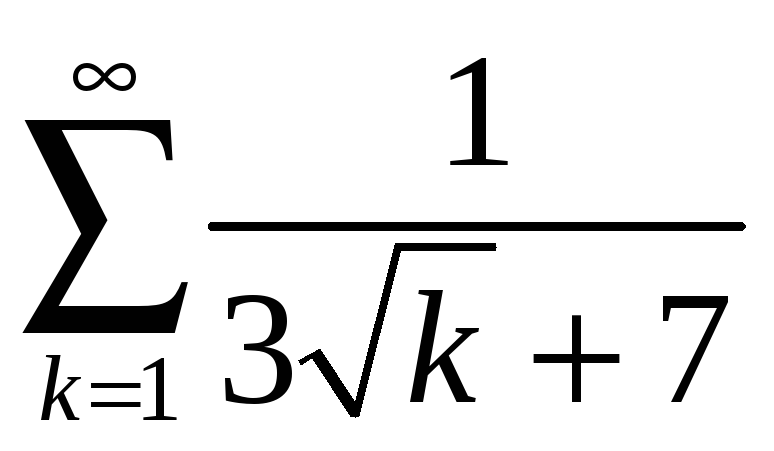 ; б)
; б)
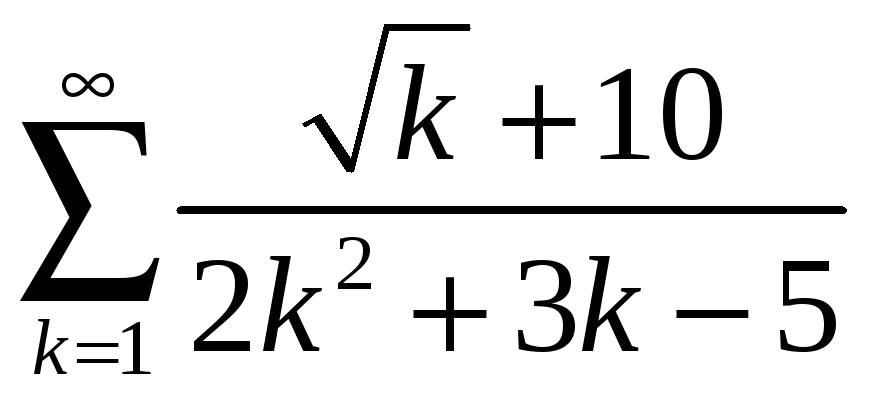 .
.
2 Исследовать сходимость ряда с помощью признака Даламбера
2.1
а)![]() ; б)
; б)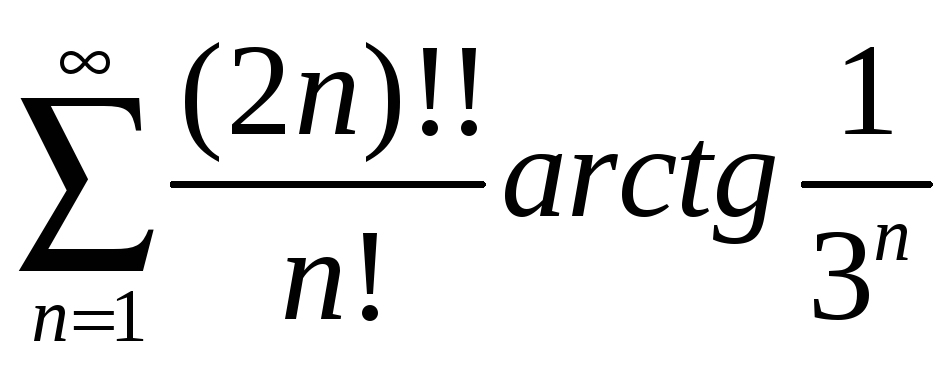 ;
;
2.2
а)![]() ; б)
; б)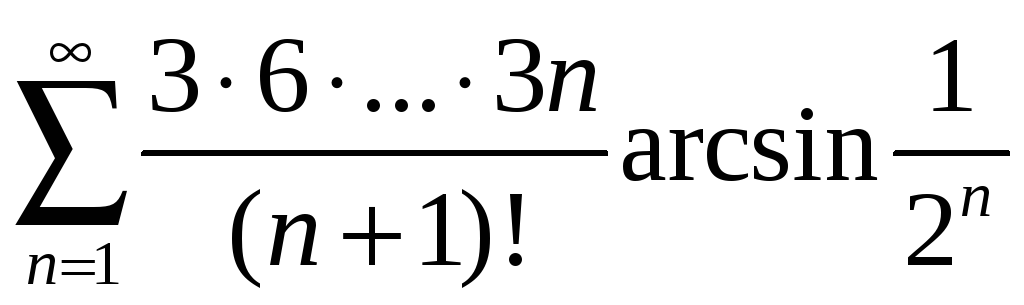 ;
;
2.3
а)![]() ; б)
; б)![]() ;
;
2.4
а)![]() ; б)
; б)![]() ;
;
2.5
а)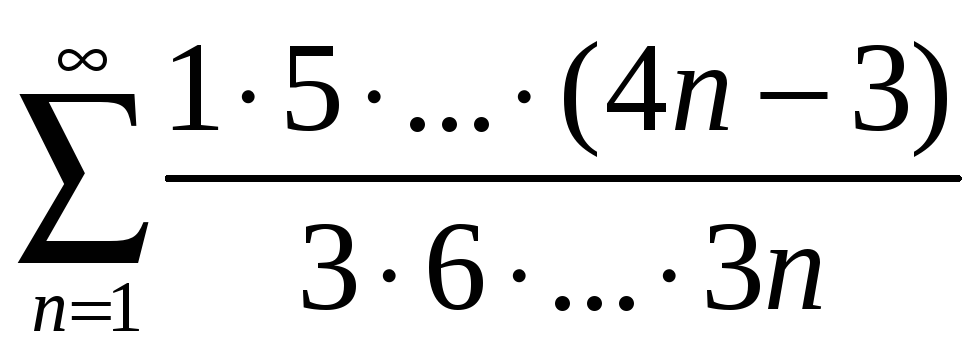 ; б)
; б)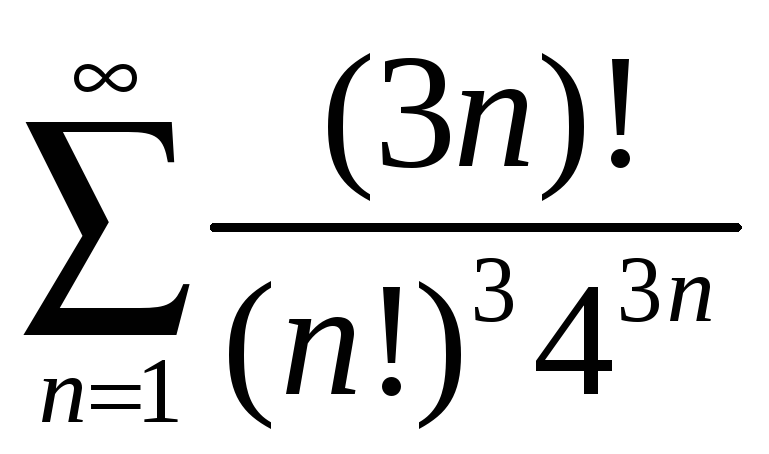 ;
;
2.6
а)![]() ; б)
; б)![]() ;
;
2.7
а)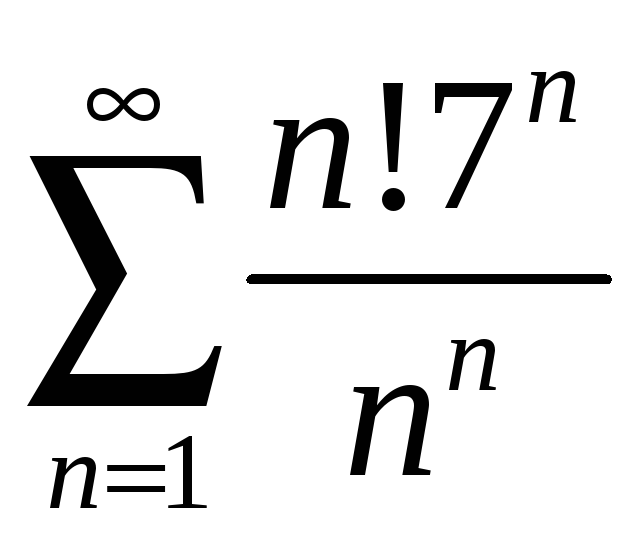 ; б)
; б)![]() ;
;
2.8
a)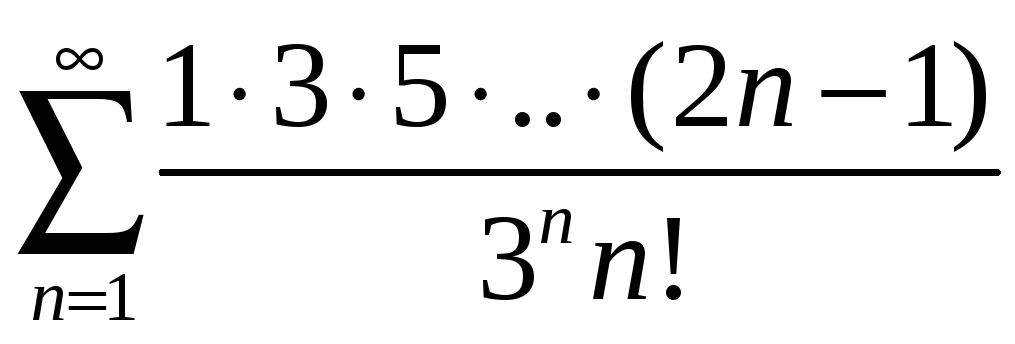 ; б)
; б)
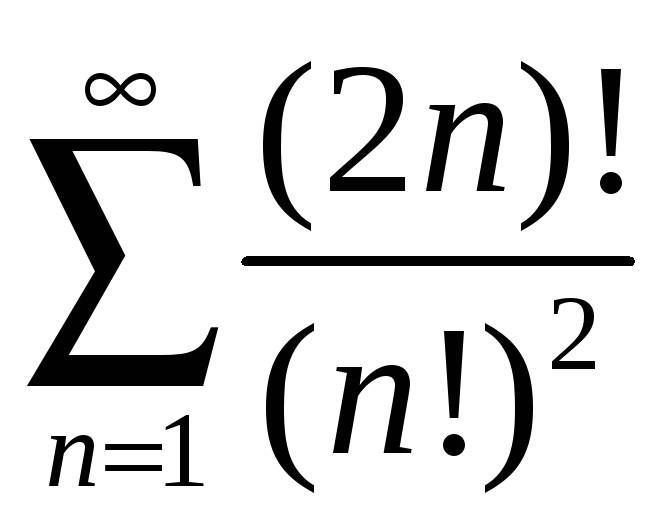 ;
;
2.9
a)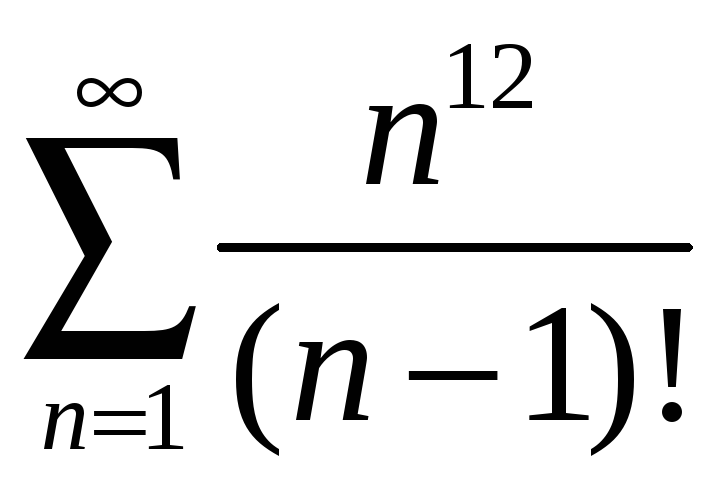 ; б)
; б)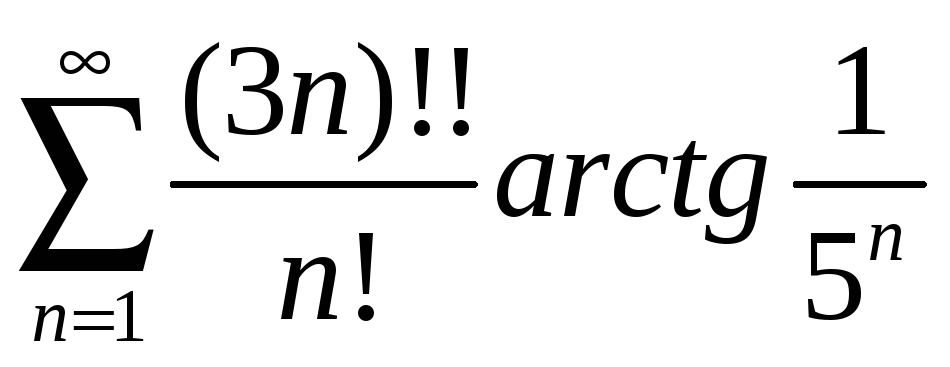 ;
;
2.10
a)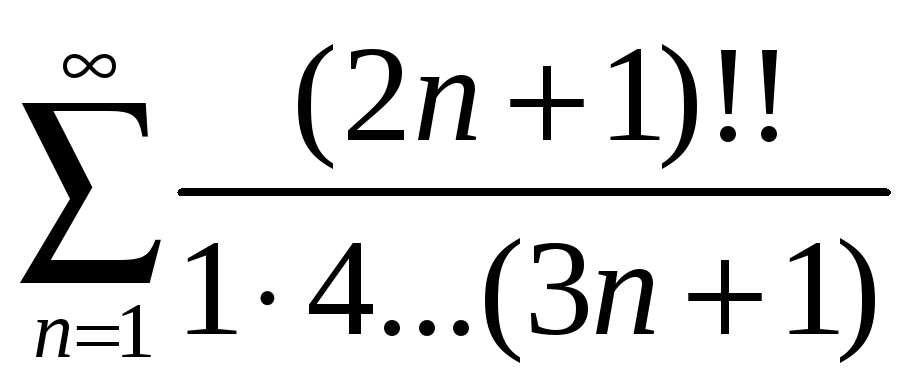 ; б)
; б)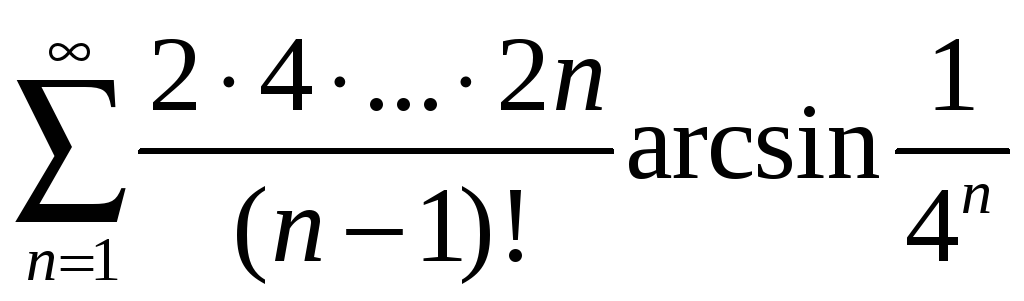 .
.
3 Исследовать сходимость ряда с помощью признака Коши
3.1
а)
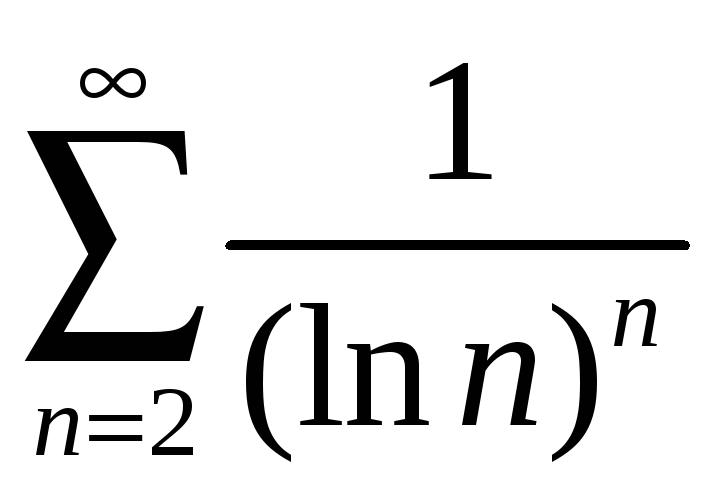 ; б)
; б)
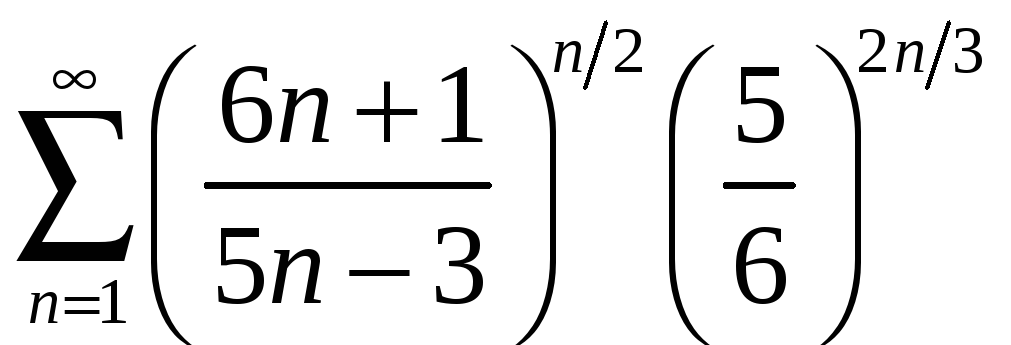 ;
;
3.2
а)
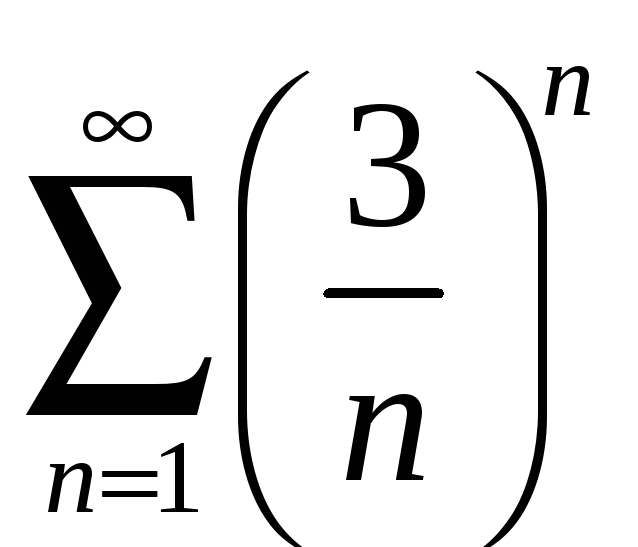 ; б)
; б)
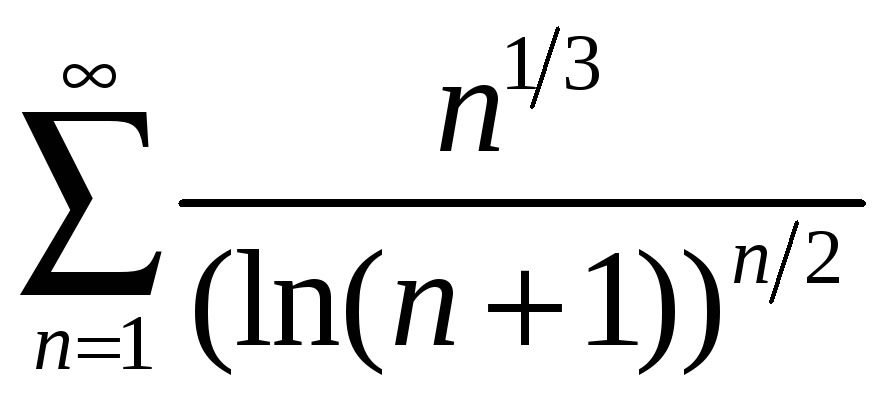 ;
;
3.3
а)
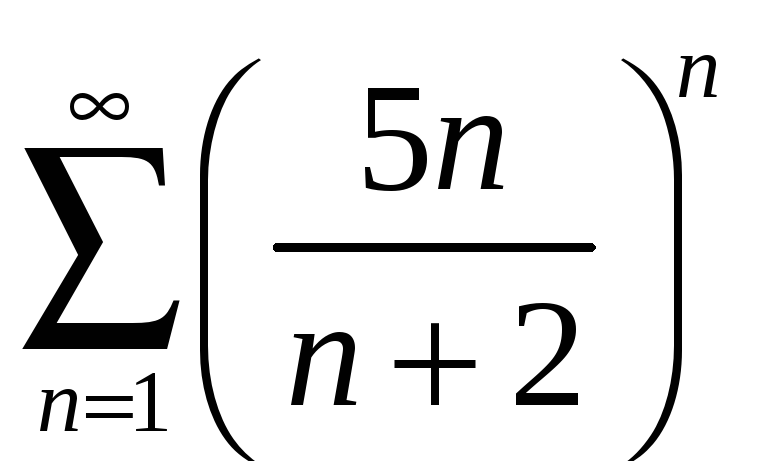 ; б)
; б)
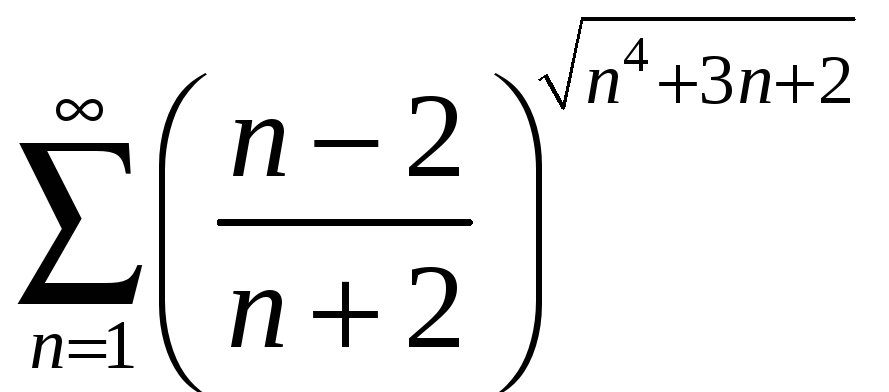 ;
;
3.4
а)
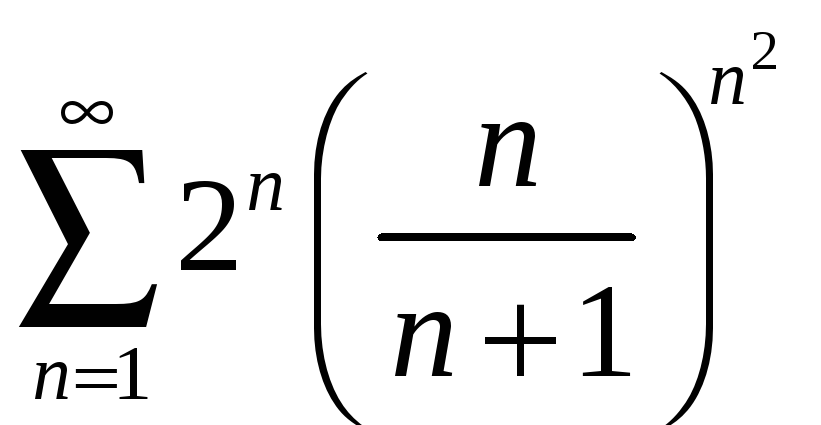 ; б)
; б)
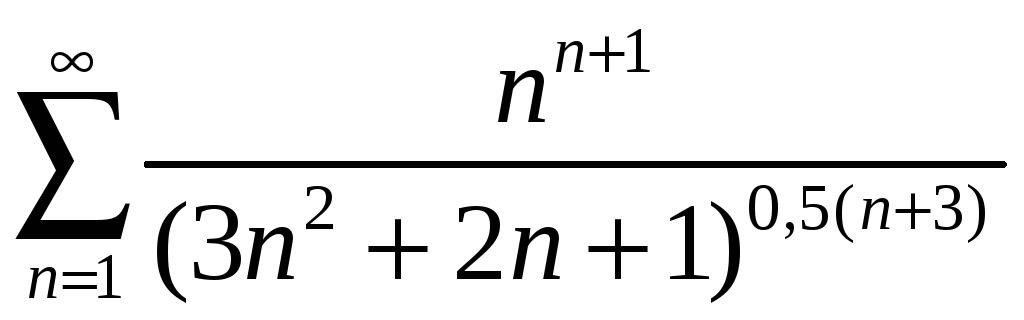 ;
;
3.5
а)
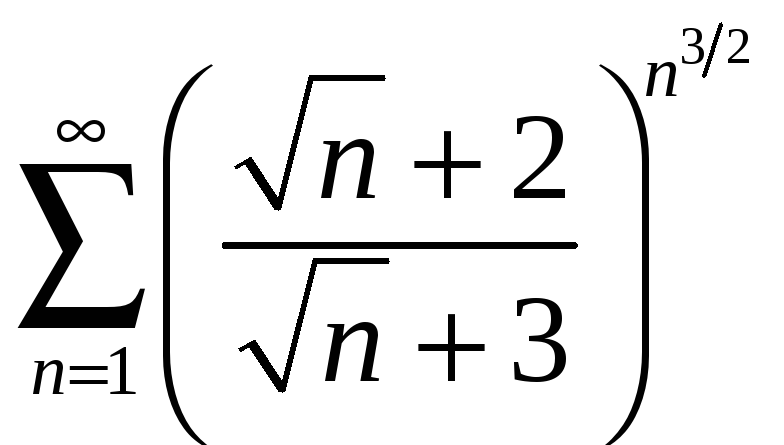 ; б)
; б)
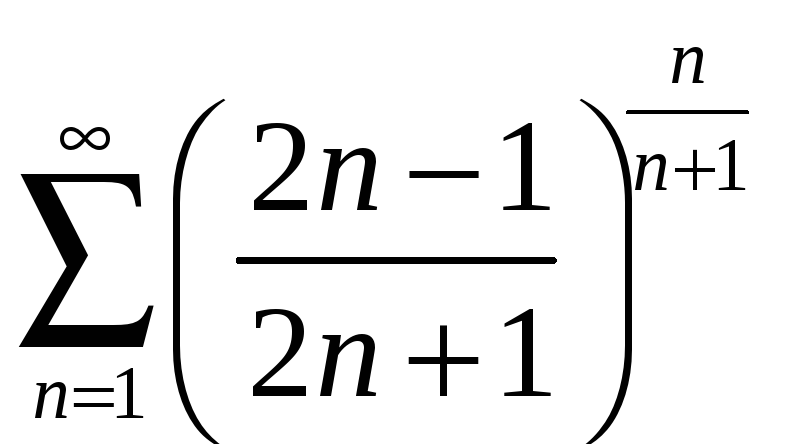 ;
;
3.6
а)
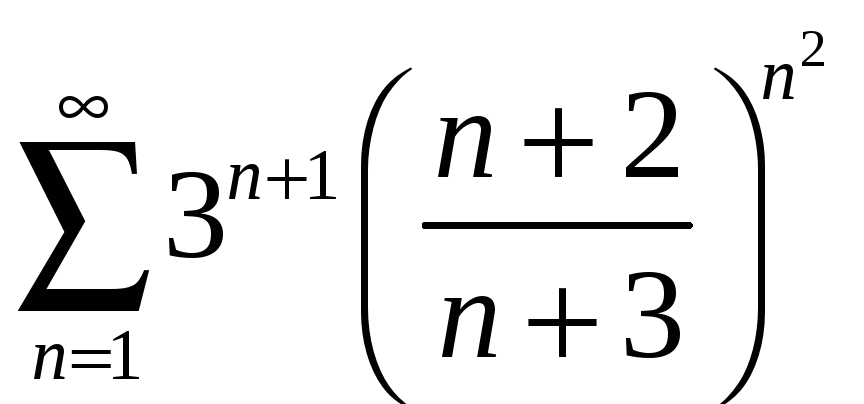 ; б)
; б)
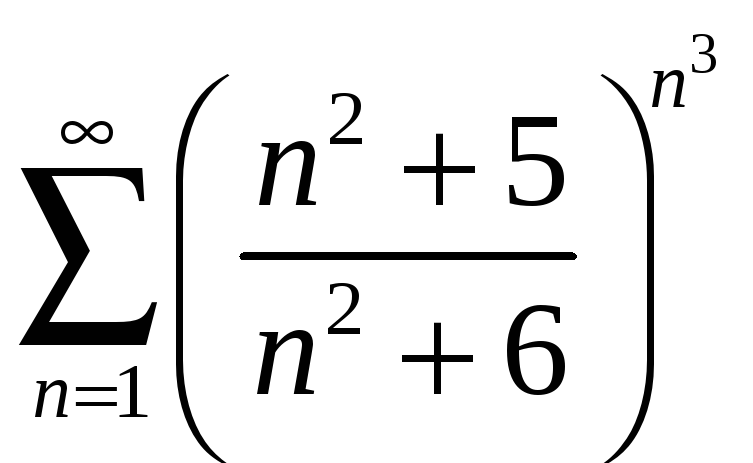 ;
;
3.7 а)
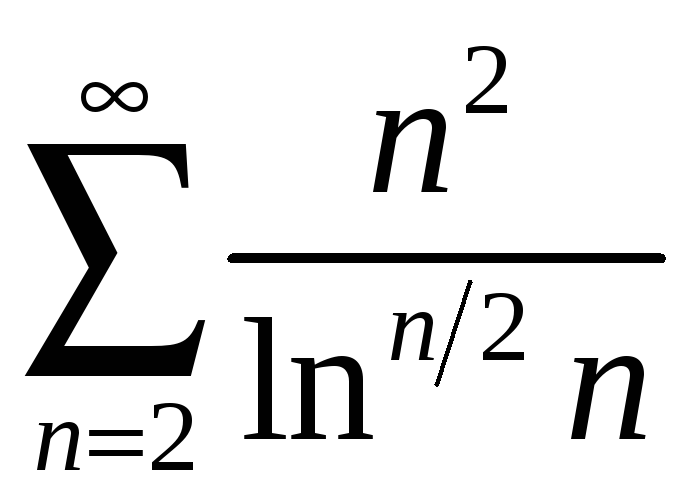 ; б)
; б)
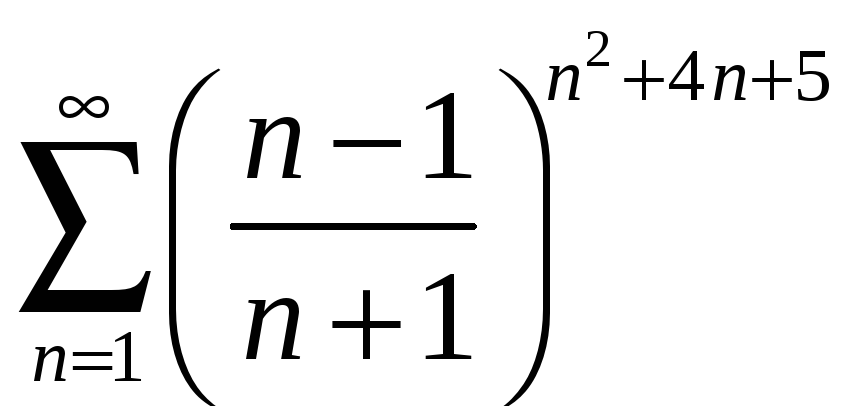 ;
;
3.8 а)
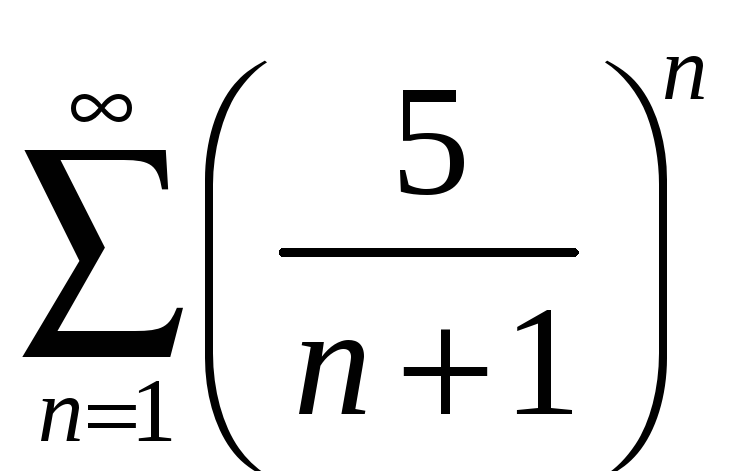 ; б)
; б)
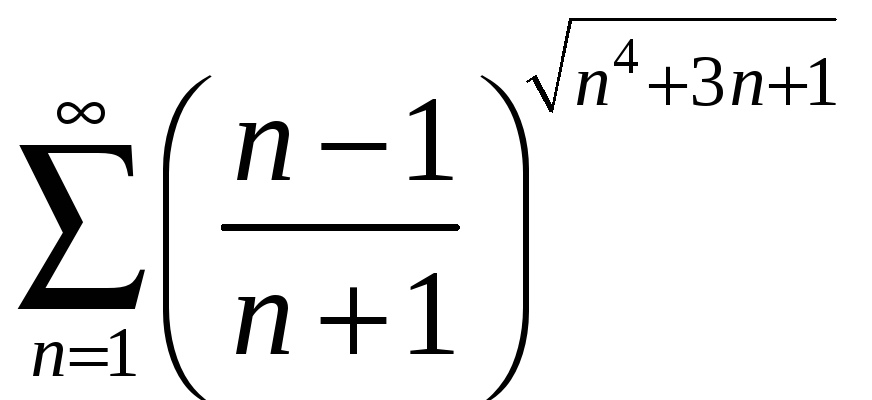 ;
;
3.9
а)
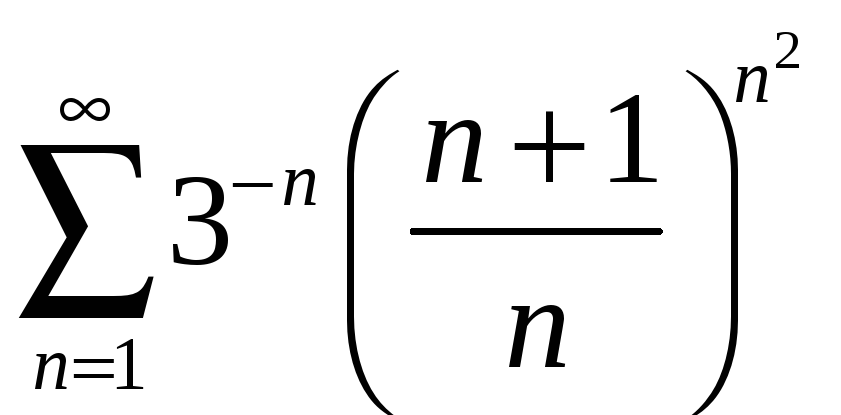 ; б)
; б)
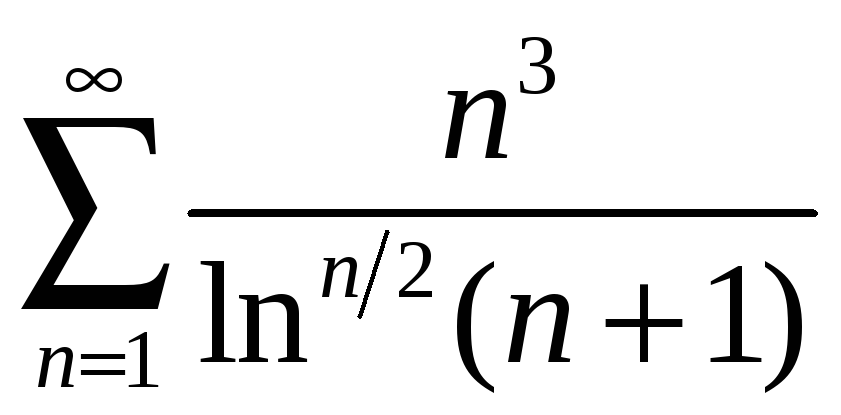 ;
;
3.10
а)
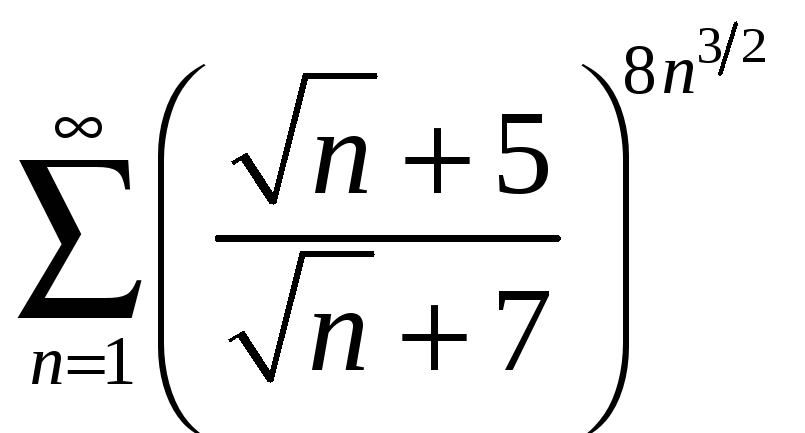 ; б)
; б)
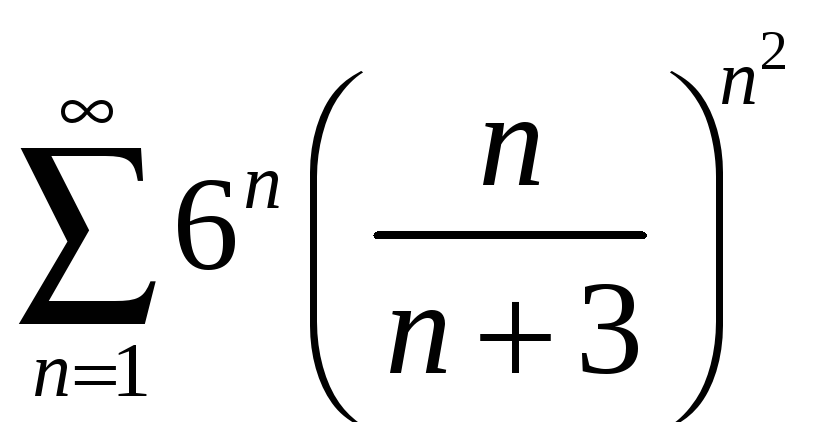
4 Исследовать сходимость ряда с помощью интегрального признака
4.1
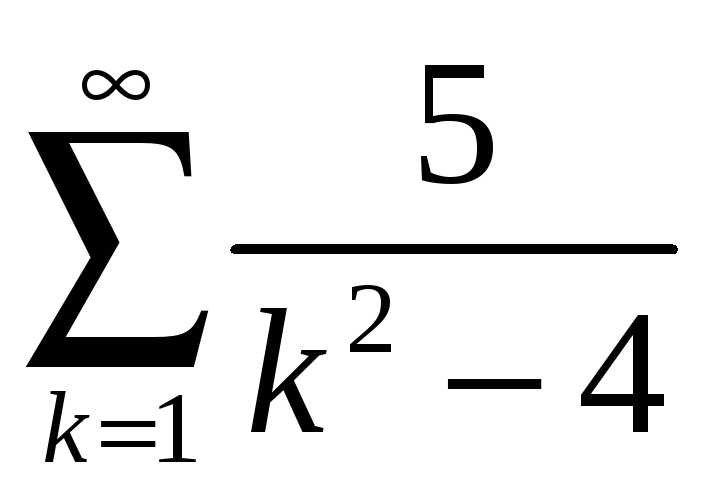 ; 4.6
; 4.6
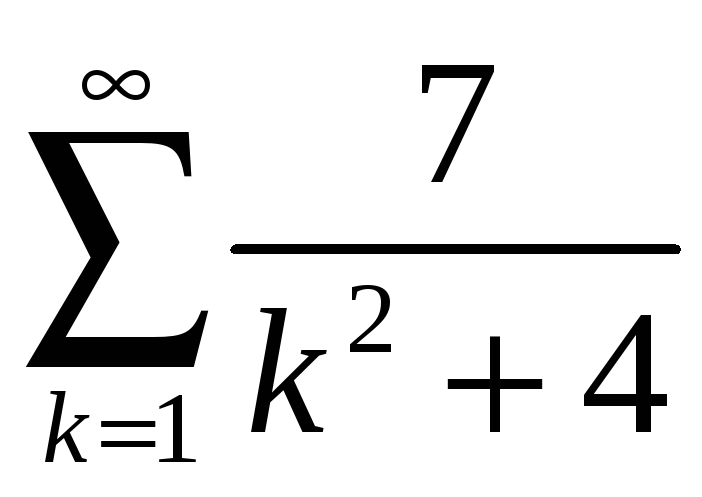 ;
;
4.2
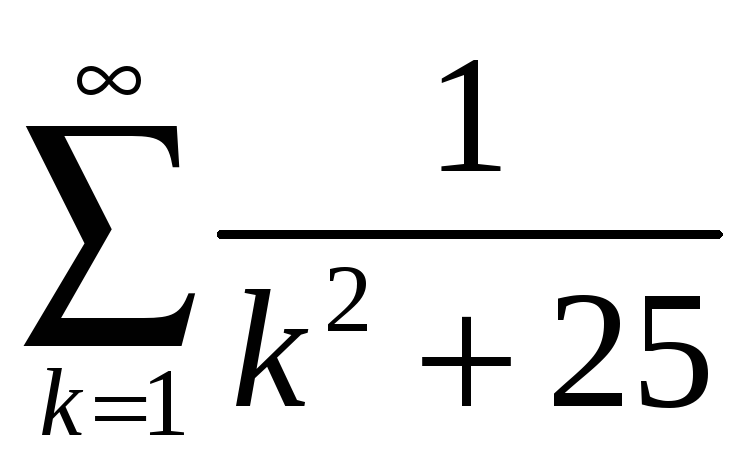 ; 4.7
; 4.7
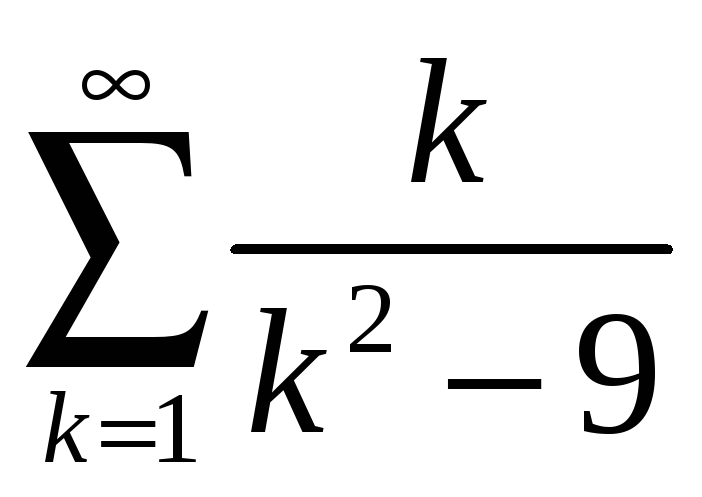 ;
;
4.3
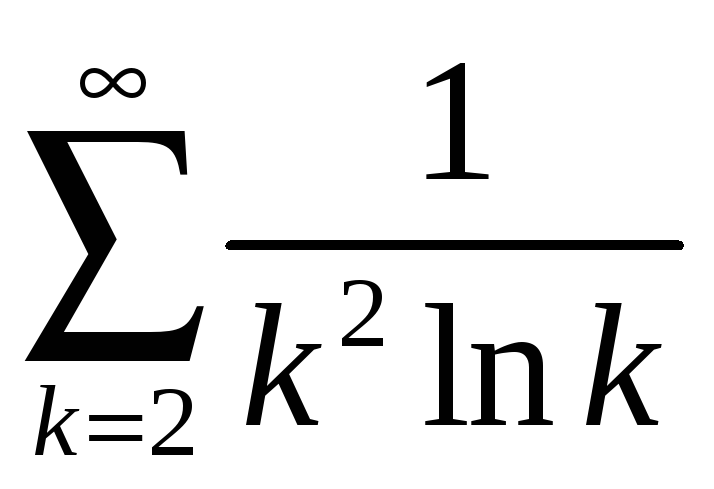 ; 4.8
; 4.8
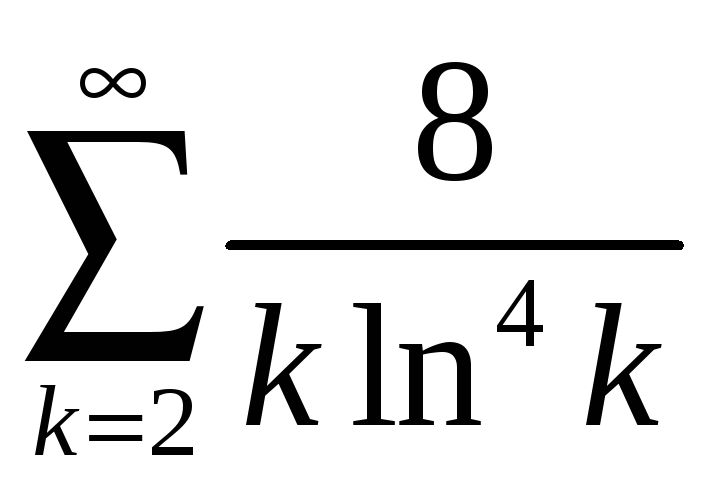 ;
;
4.4
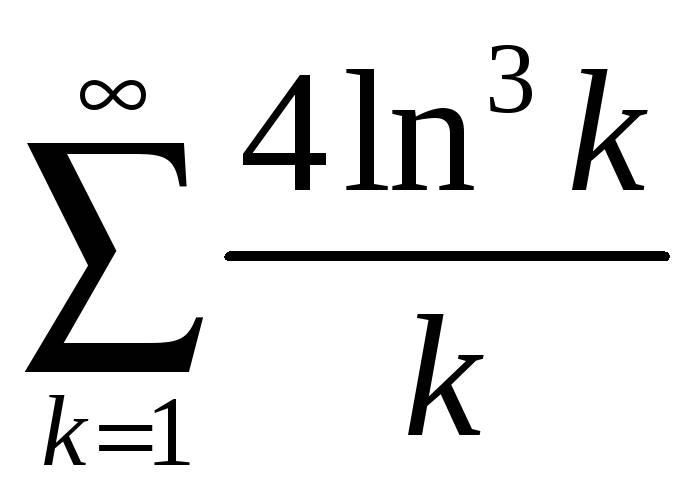 ; 4.9
; 4.9
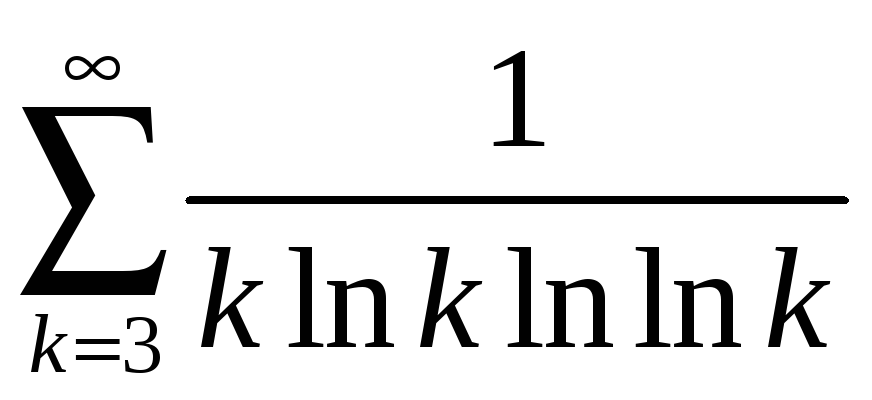 ;
;
4.5
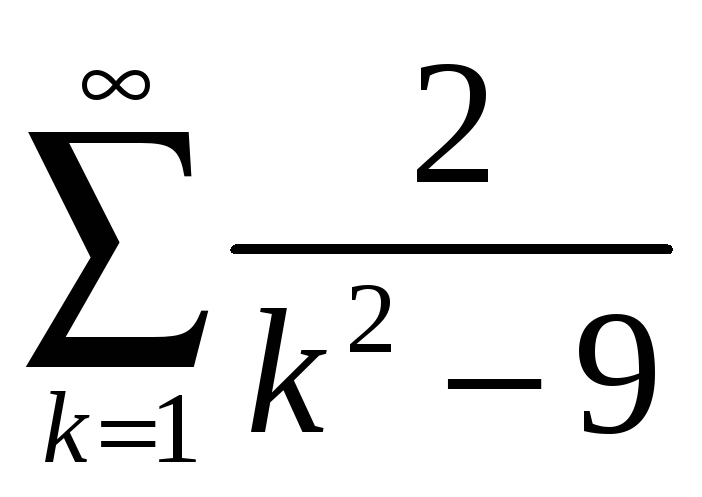 ; 4.10
; 4.10
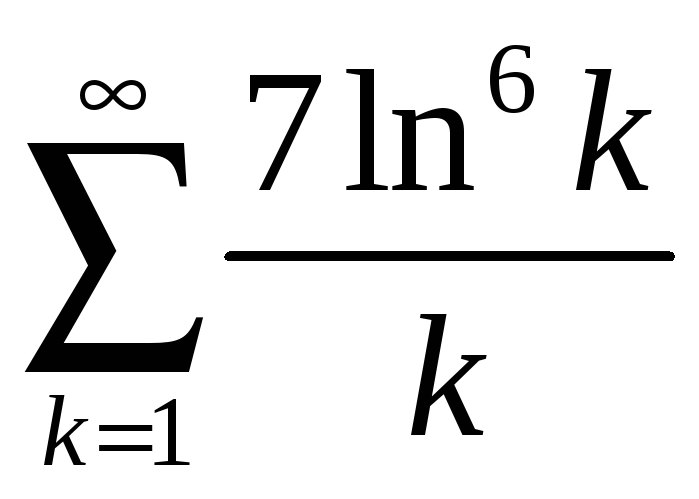 .
.
5 Найти
все значения
![]() ,
при которых сходится ряд
,
при которых сходится ряд
5.1
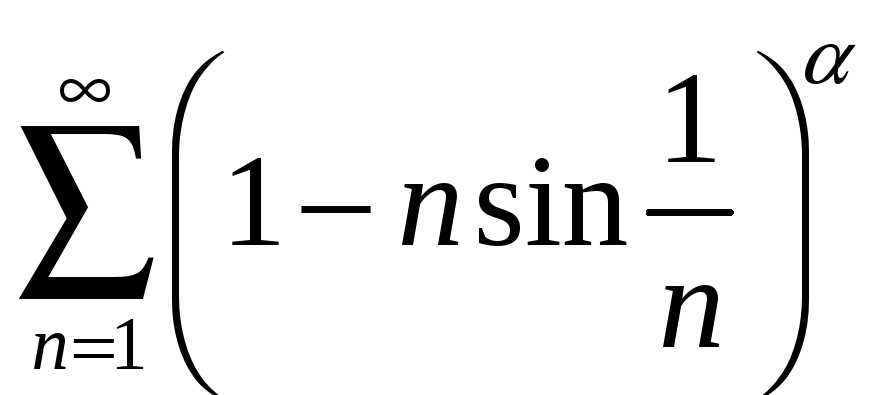 ; 5.6
; 5.6
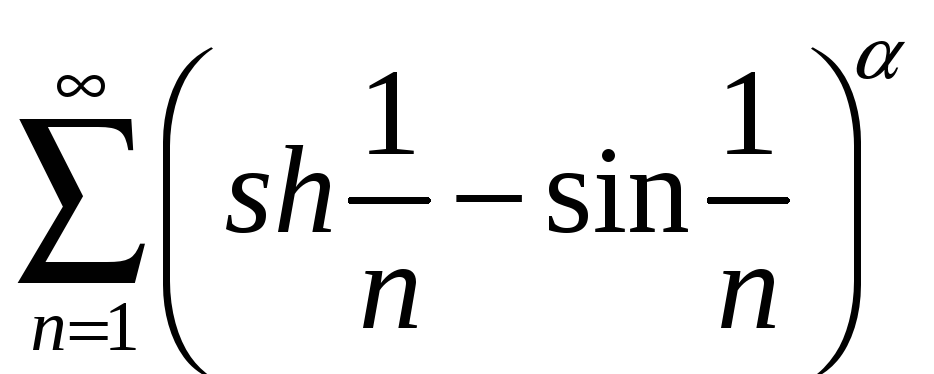 ;
;
5.2
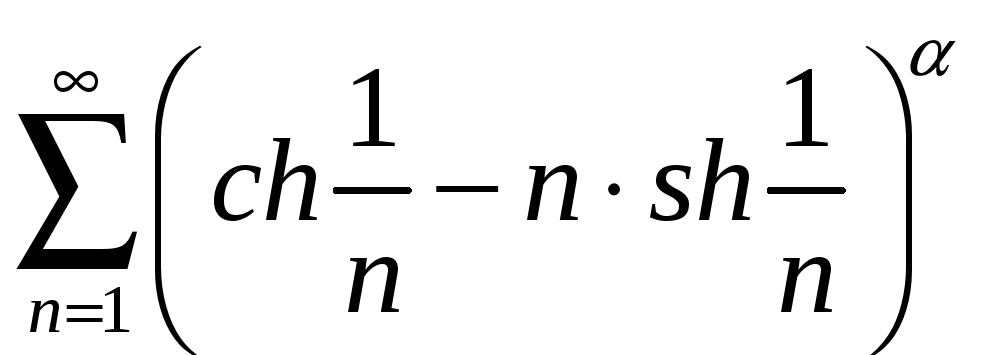 ; 5.7
; 5.7
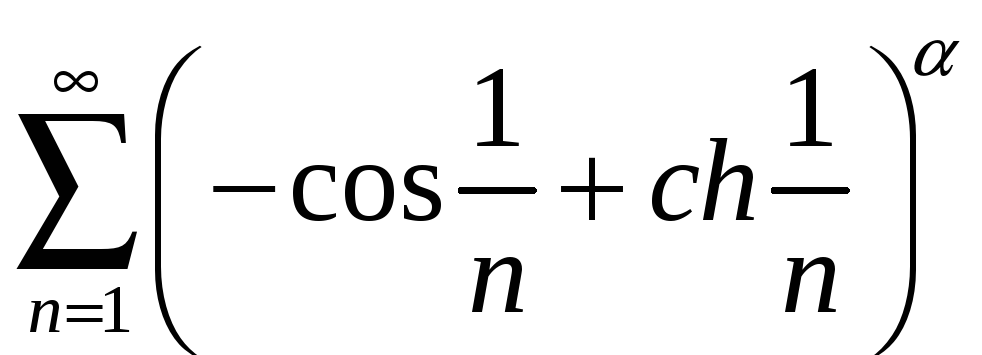 ;
;
5.3
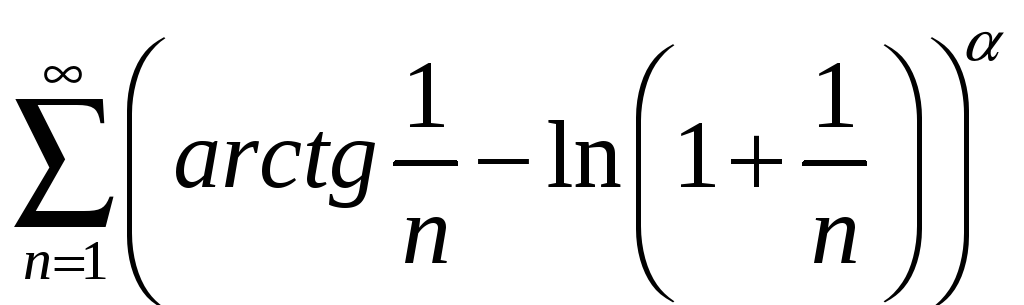 ; 5.8
; 5.8
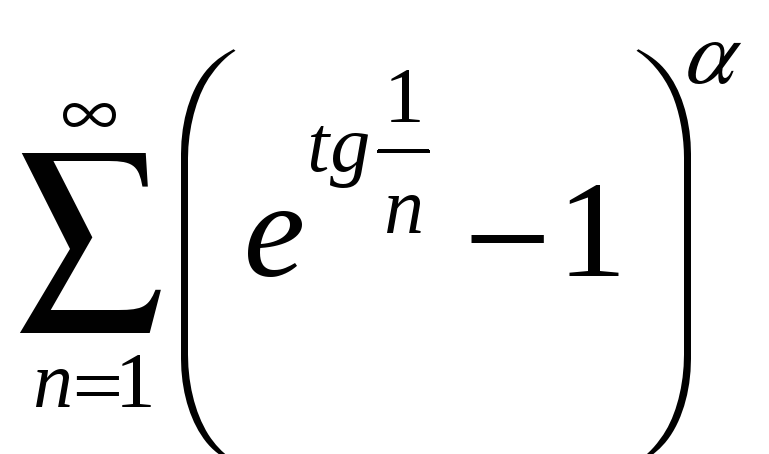 ;
;
5.4
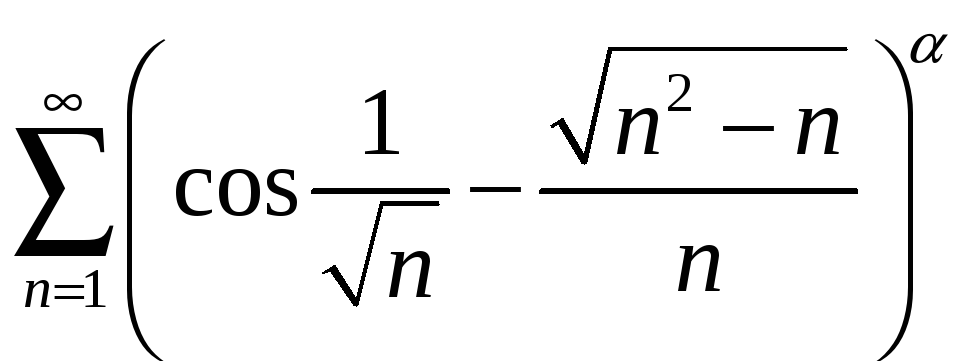 ; 5.9
; 5.9
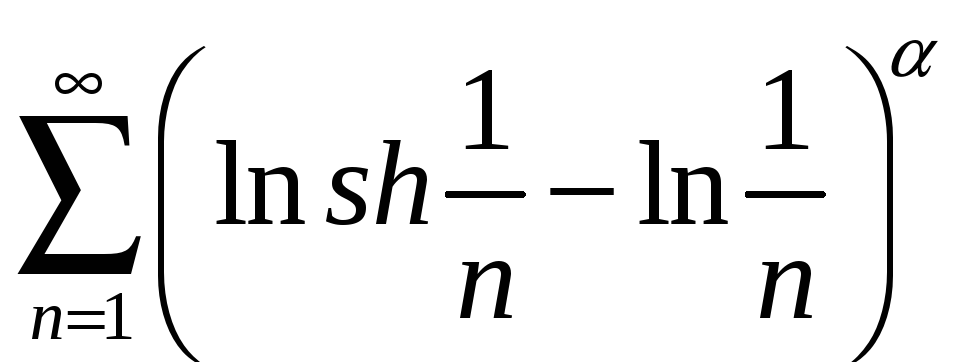 ;
;
5.5
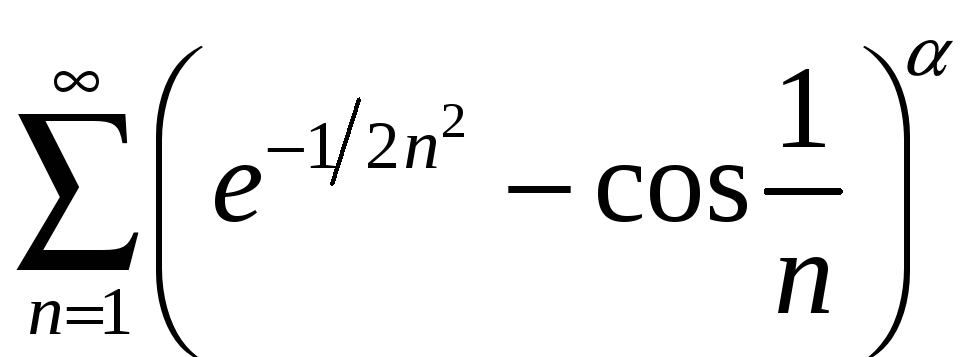 ; 5.10
; 5.10
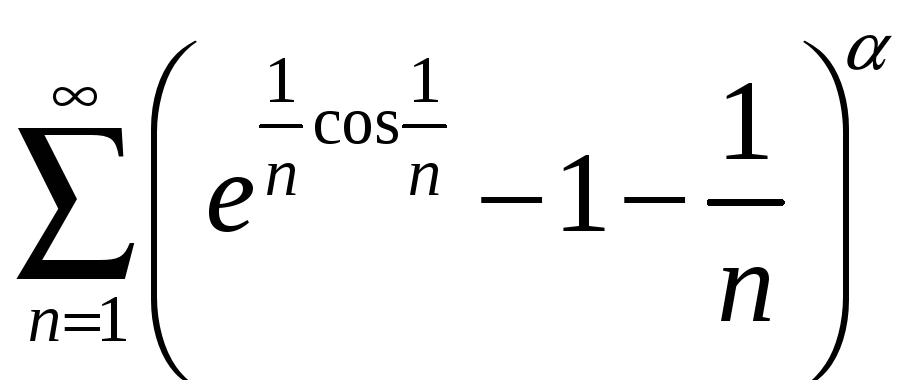 .
.
6 Исследовать сходимость ряда
6.1
а)
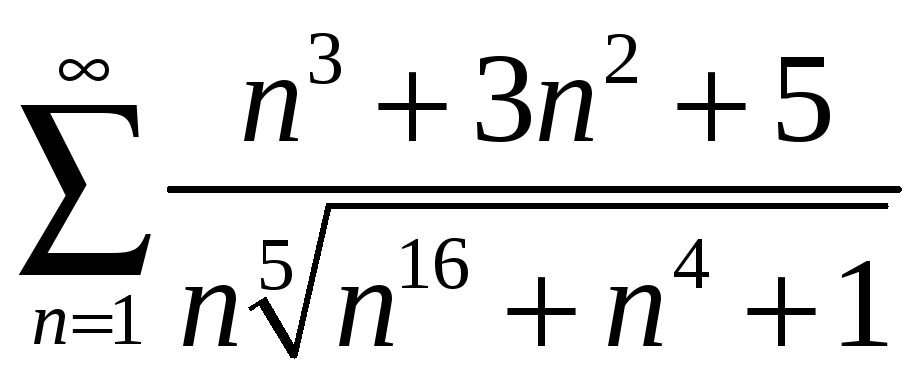 ;
б)
;
б)
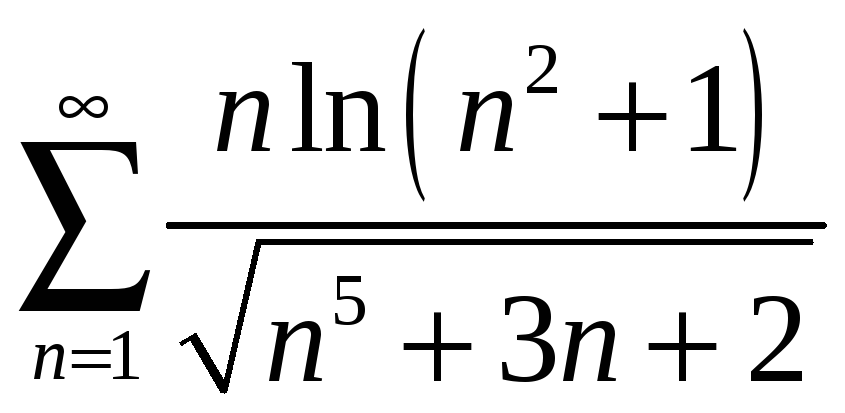 ;
;
6.2
а)
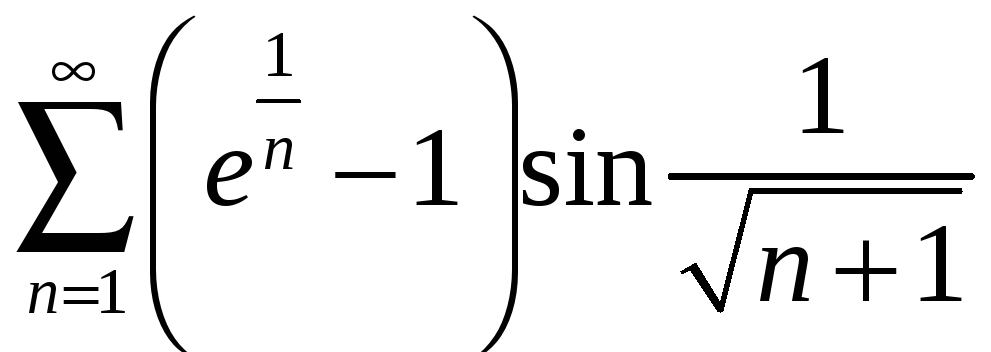 ;
б)
;
б)
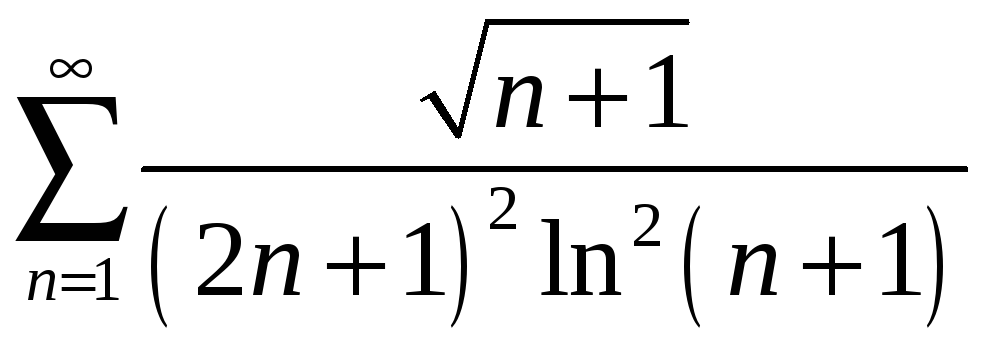 ;
;
6.3
а)
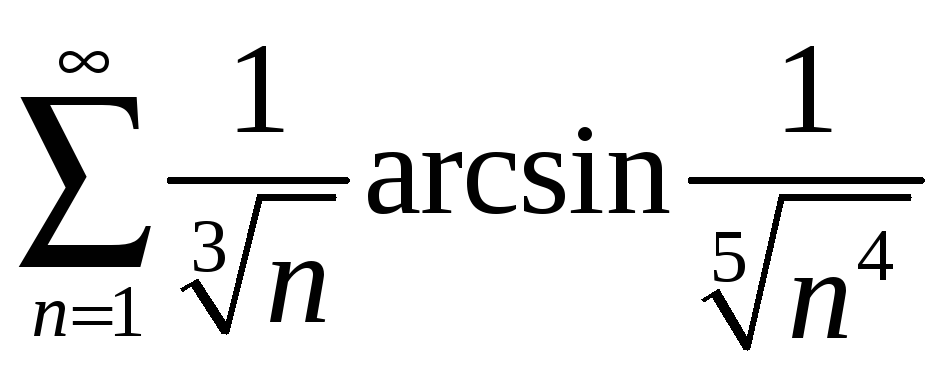 ;
б)
;
б)
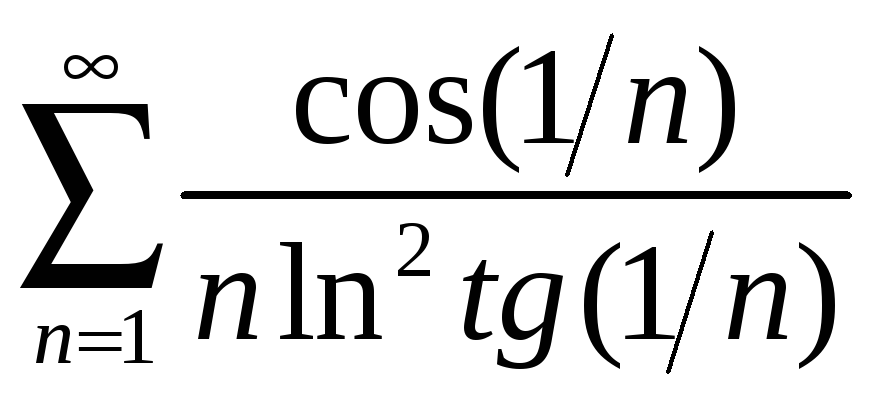 ;
;
6.4
а)
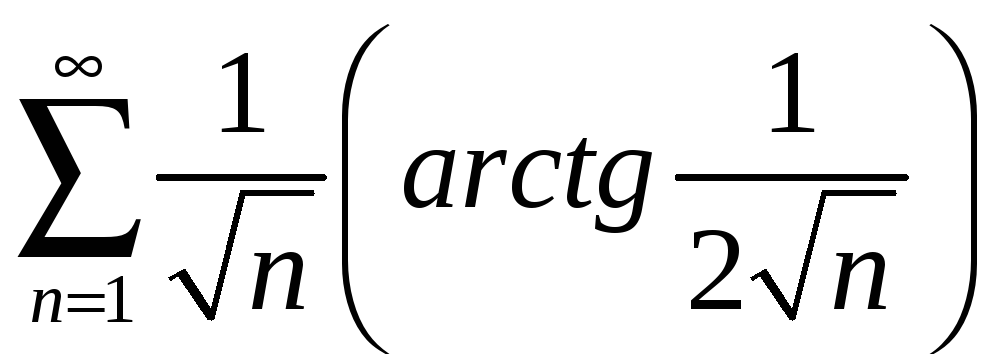 ;
б)
;
б)
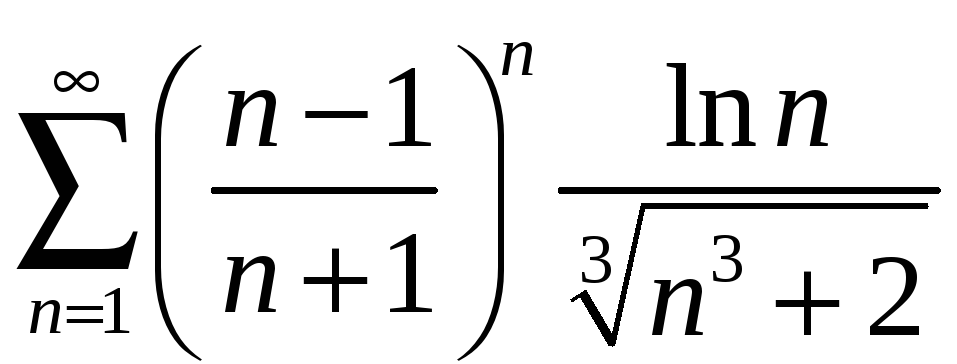 ;
;
6.5
а)
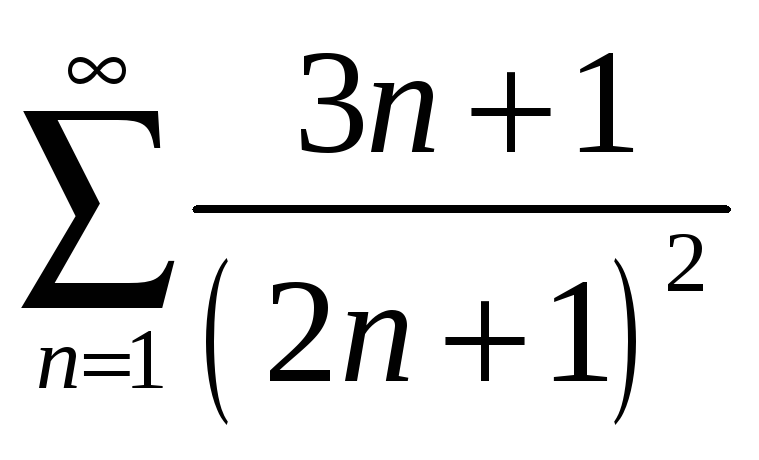 ; б)
; б)
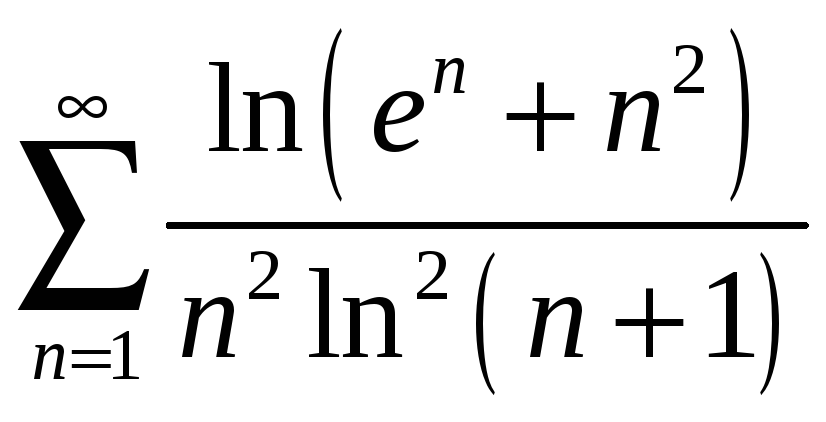 ;
;
6.6
а)
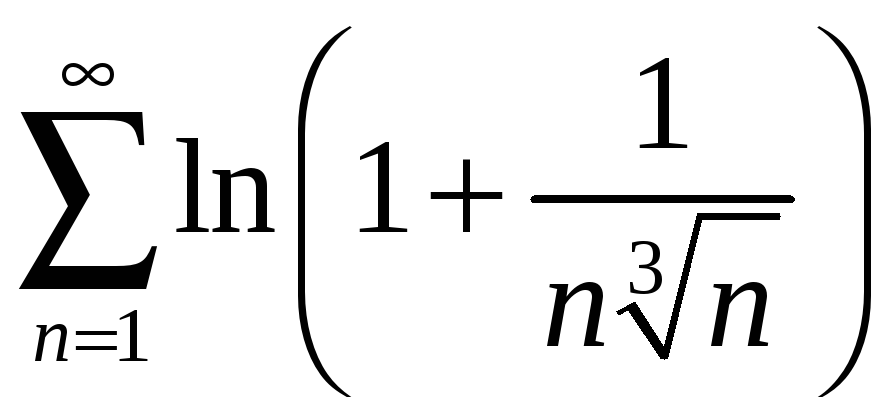 ; б)
; б)
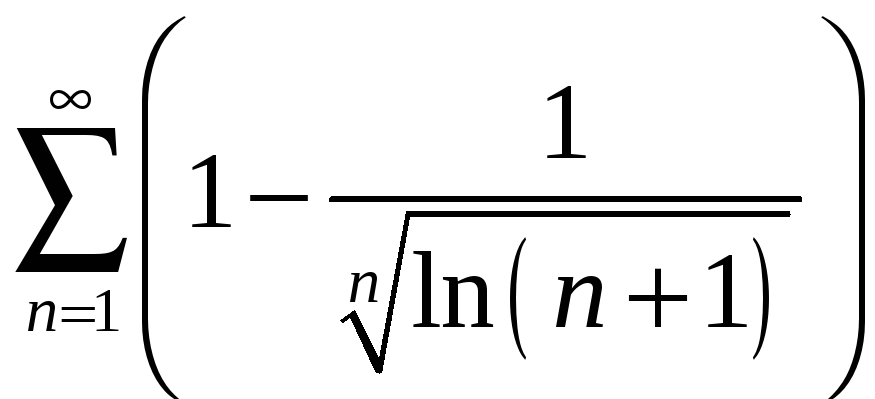 ;
;
6.7 а)
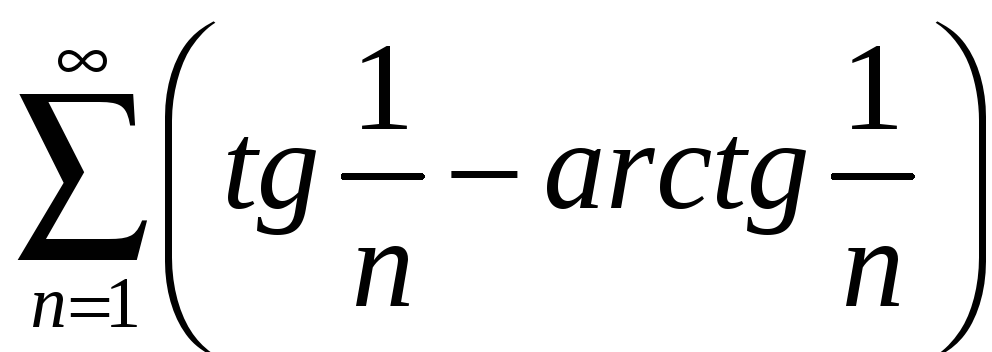 ; б)
; б)
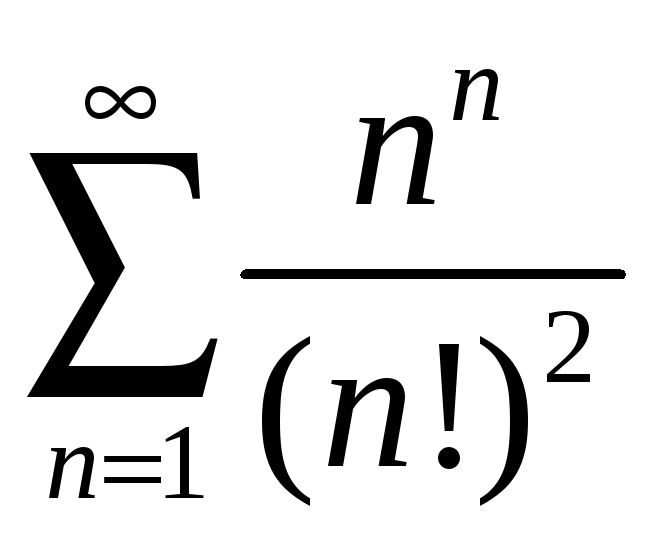 ;
;
6.8 а)
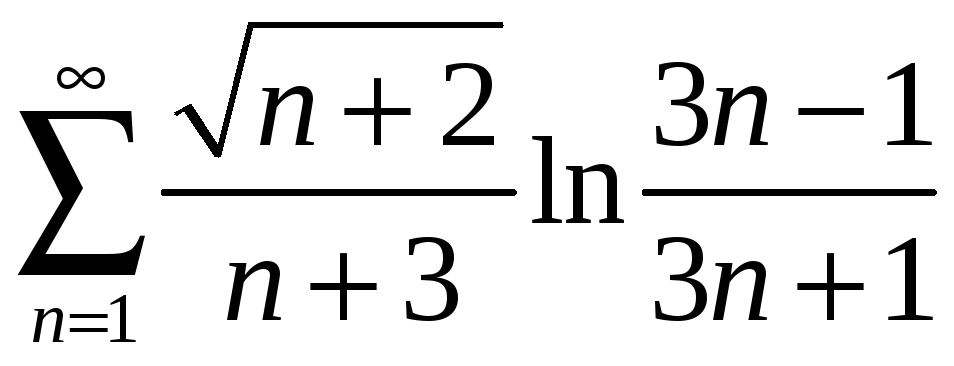 ; б)
; б)
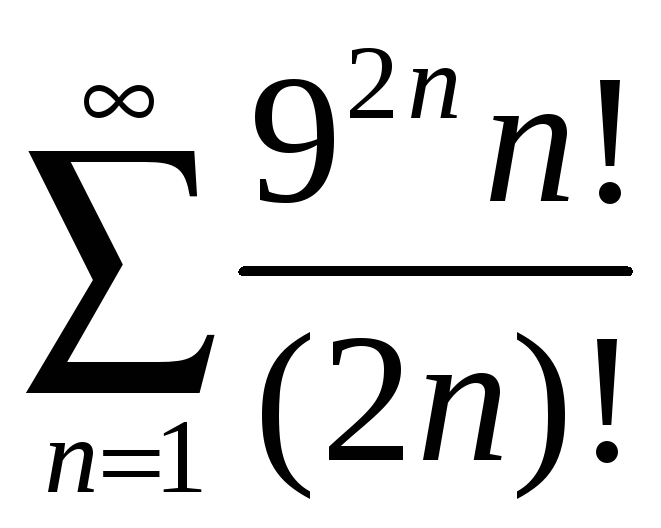 ;
;
6.9
а)
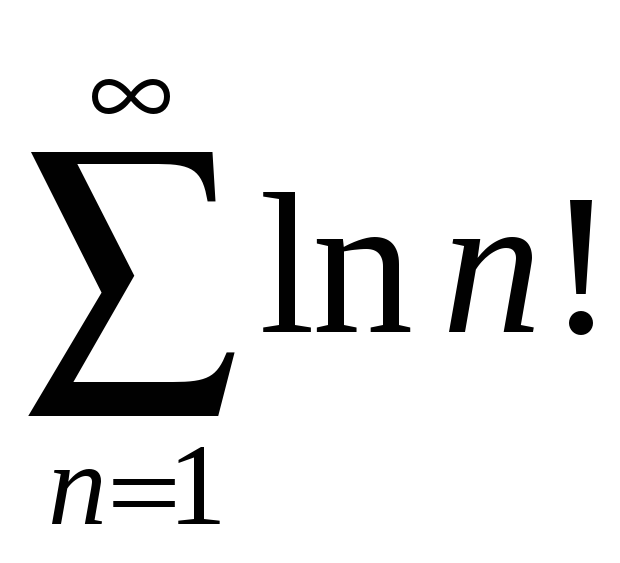 ; б)
; б)
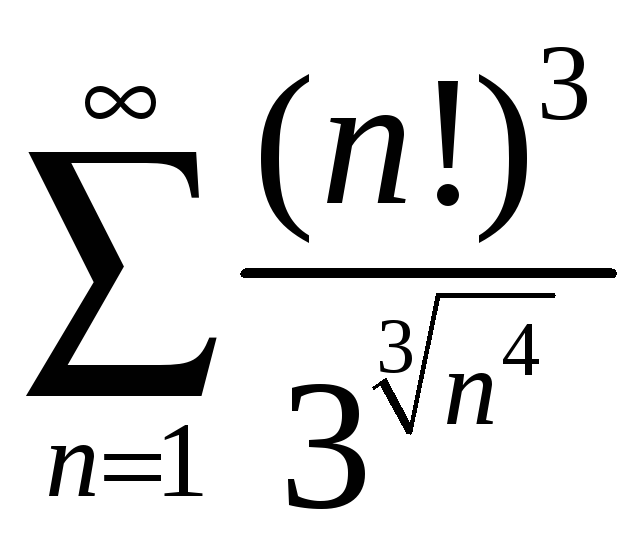 ;
;
6.10
а)
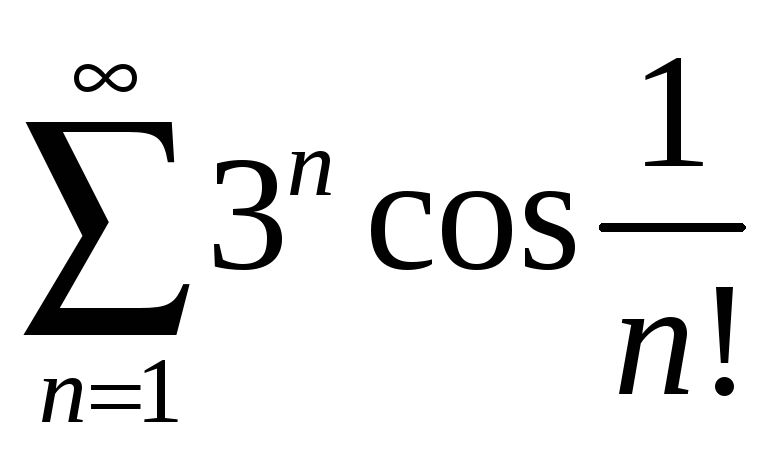 ; б)
; б)
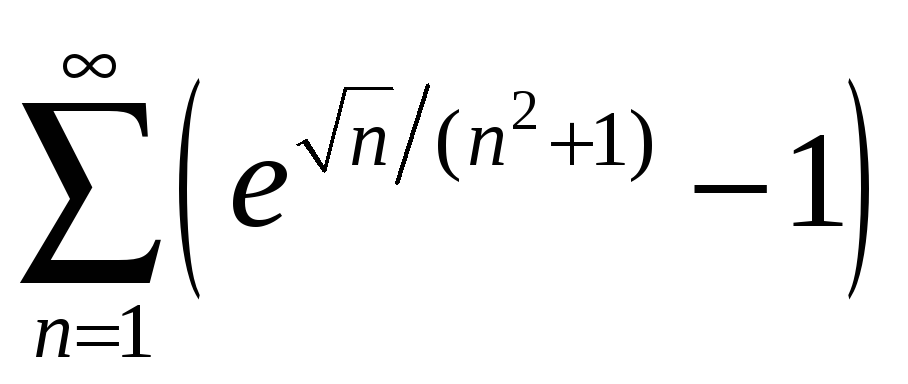 .
.
7 Доказать:
7.1
Если
![]() ,
ряд
,
ряд![]()
![]() сходится
и
сходится
и
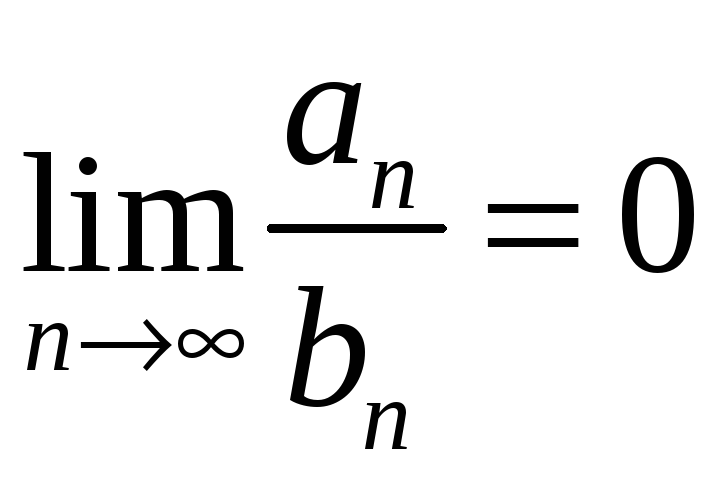 ,
то ряд
,
то ряд
![]() также сходится.
также сходится.
7.2
Если
![]() ,
ряд
,
ряд
![]()
![]() расходится,
расходится,
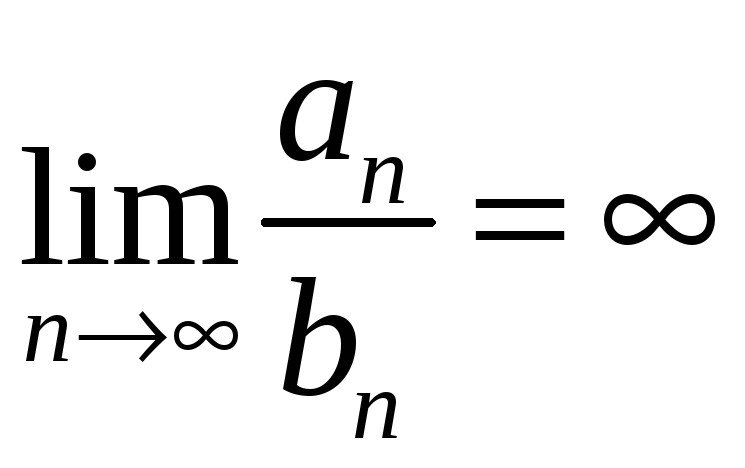 ,
то ряд
,
то ряд
![]() -
-
расходится.
7.3
Если существует
![]() ,
то
,
то
![]()
![]() расходится.
расходится.
7.4
Если
![]() и
и
![]() сходится, то
сходится, то
![]() .
.
7.5
Если
![]() и
и
![]() -
сходится, то
-
сходится, то
![]() сходится.
сходится.
7.6
Если
![]() -
ограничена и
-
ограничена и
![]() ,
то
,
то
![]() сходится.
сходится.
7.7
Если ряд![]()
![]() сходится,
то
сходится,
то
![]() остаток ряда
остаток ряда
![]() также сходится.
также сходится.
7.8
Если
![]() остаток ряда
остаток ряда
![]() сходится, то ряд
сходится, то ряд![]()
![]() сходится.
сходится.
7.9 Если
ряды
![]() и
и
![]() сходятся
и
сходятся
и
![]() ,
то сходится и ряд
,
то сходится и ряд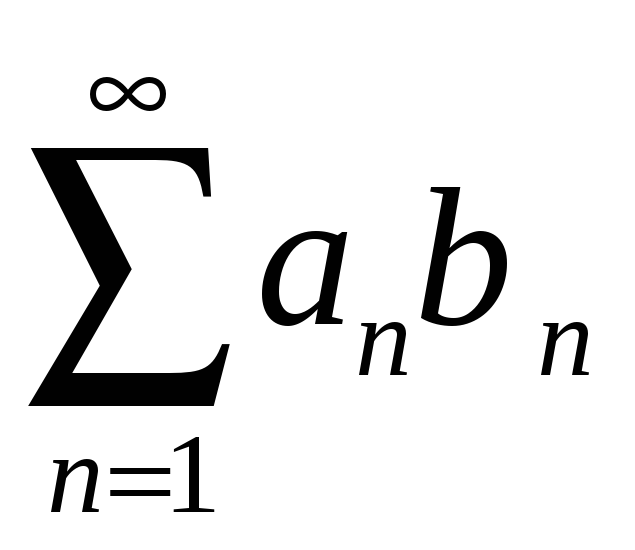 .
.
7.10
Если![]() сходится и
сходится и
![]() ,
то сходится и ряд
,
то сходится и ряд![]() .
.
Лабораторная работа 2 знакопеременные ряды
1 Доказать абсолютную сходимость ряда
1.1
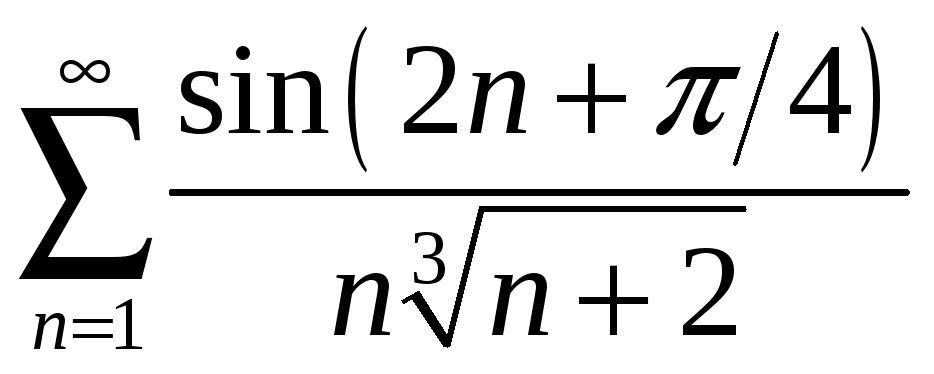 ;
;
1.2
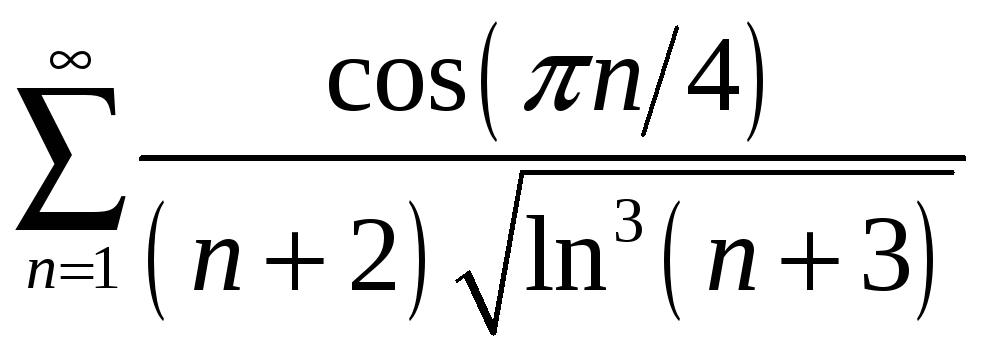 ;
;
1.3
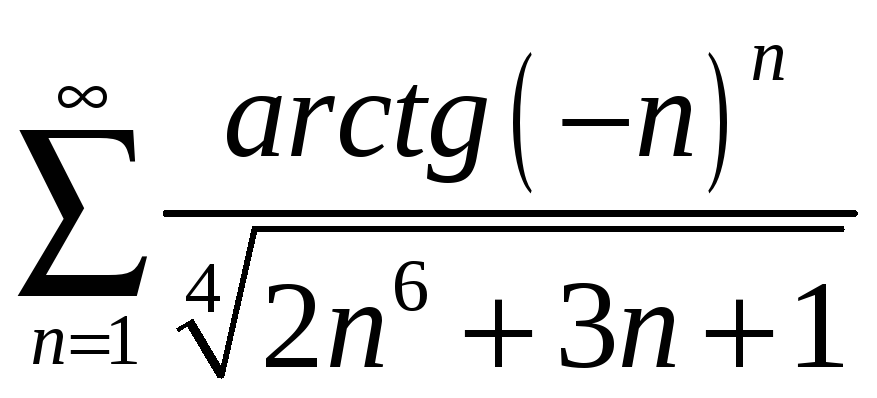 ;
;
1.4
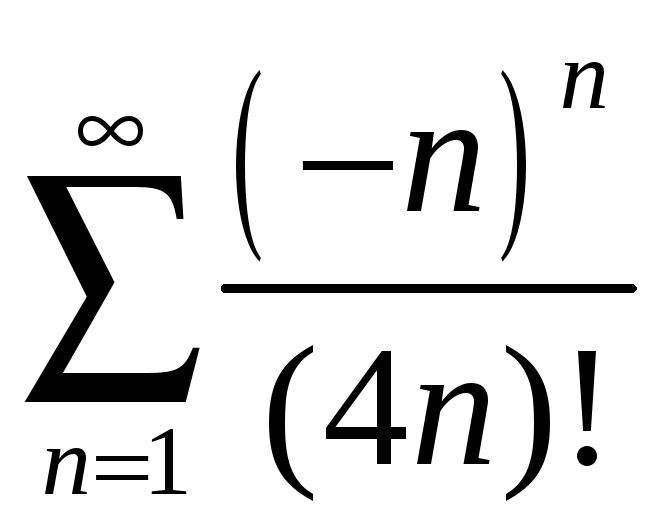 ;
;
1.5
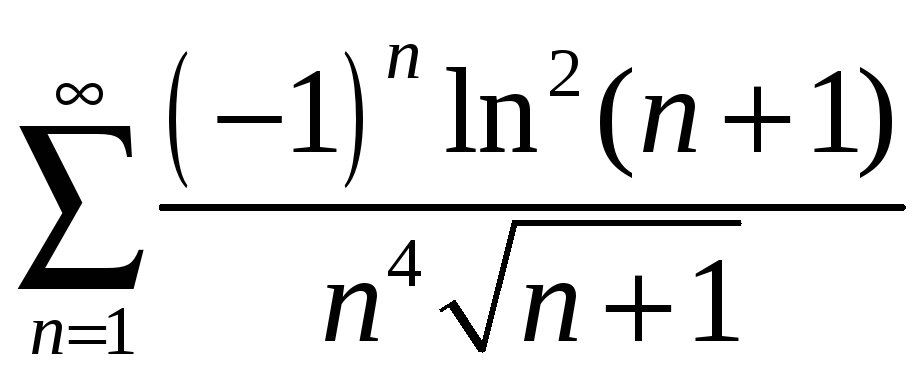 ;
;
1.6
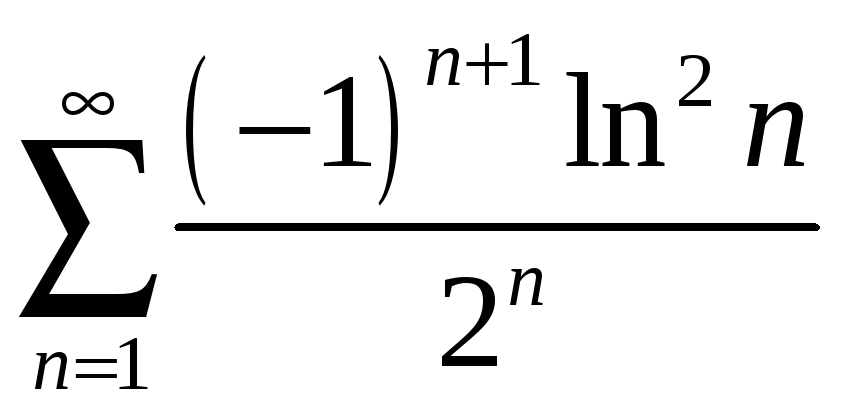 ;
;
1.7
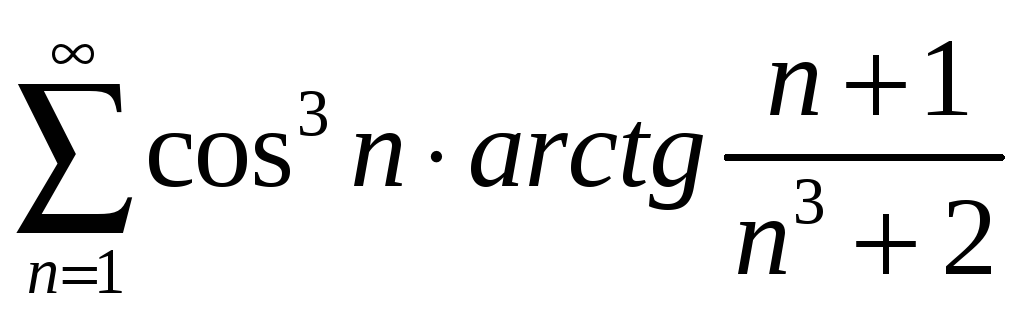 ;
;
1.8
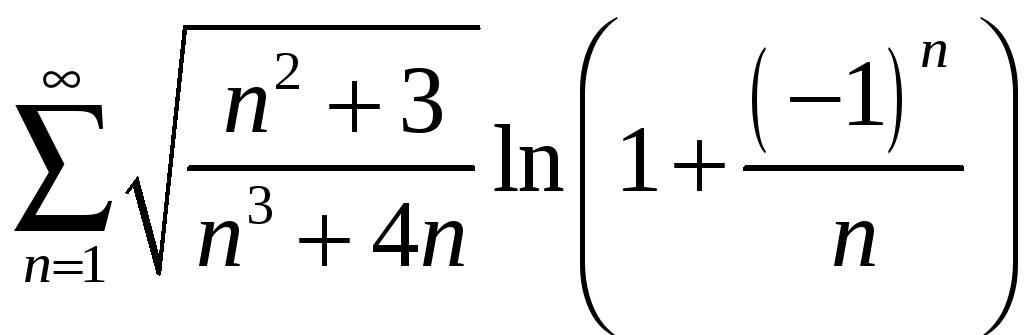 ;
;
1.9
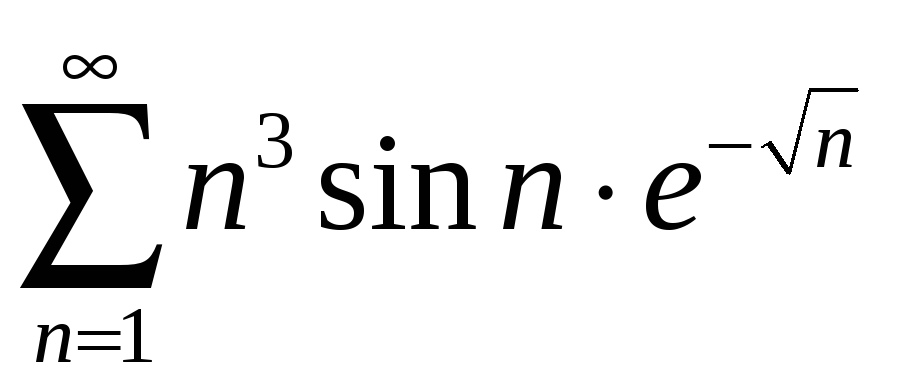 ;
;
1.10
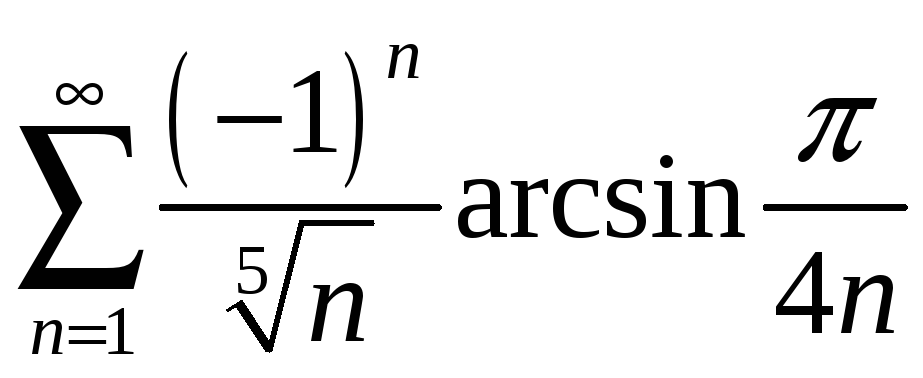 .
.
2 Исследовать сходимость и абсолютную сходимость ряда
2.1
а)
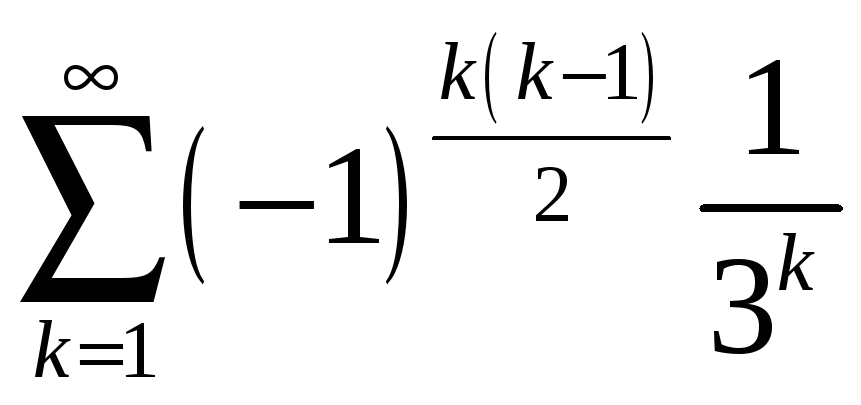 ;
б)
;
б)
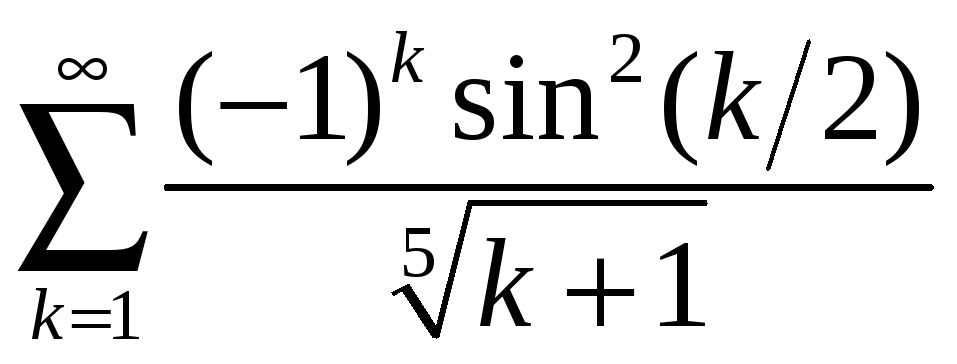 ;
;
2.2
а)
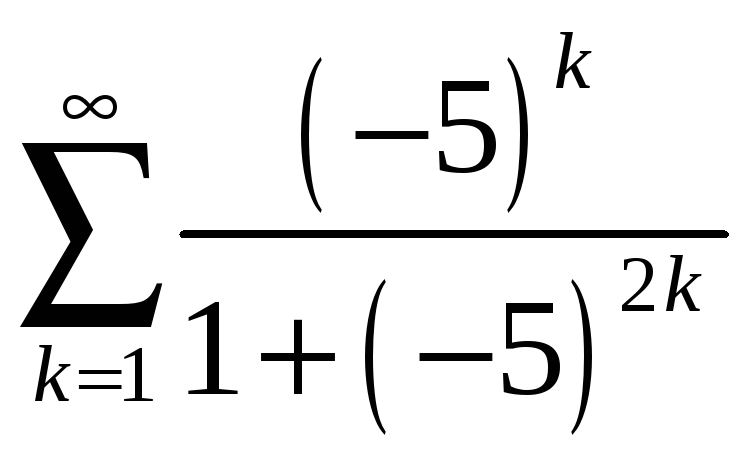 ;
б)
;
б)
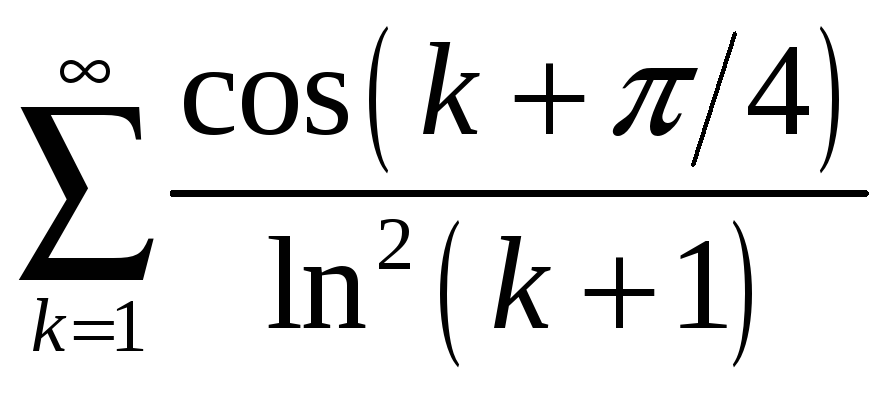 ;
;
2.3
а)
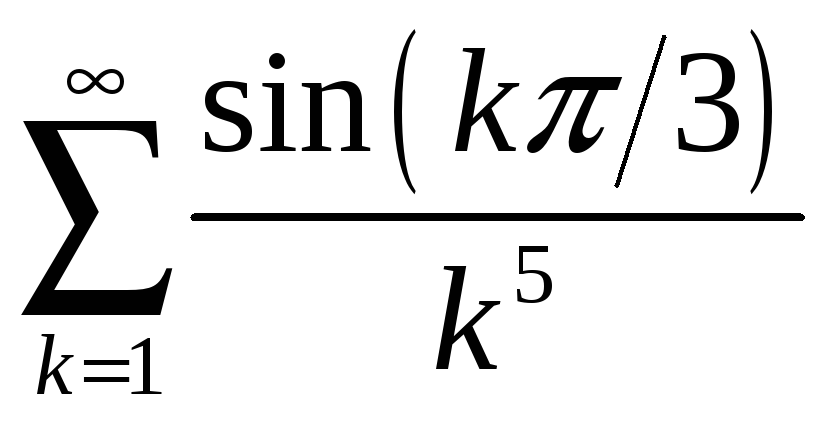 ;
б)
;
б)
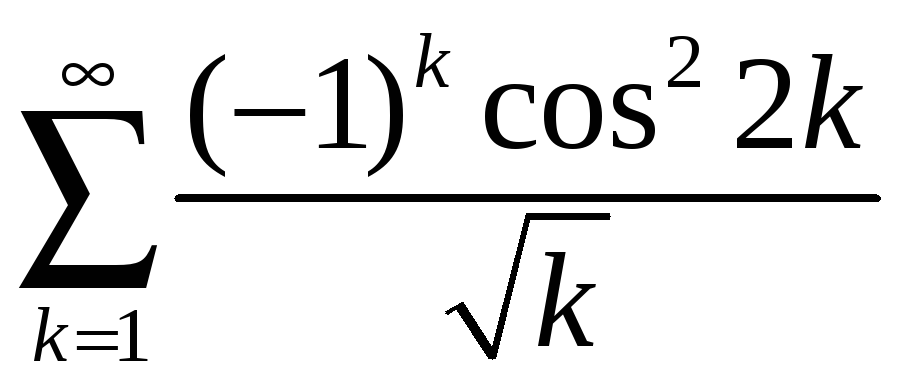 ;
;
2.4
а)
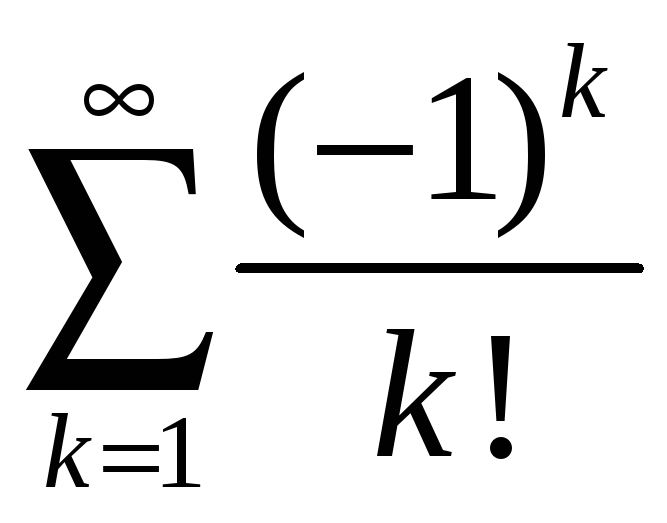 ;
б)
;
б)
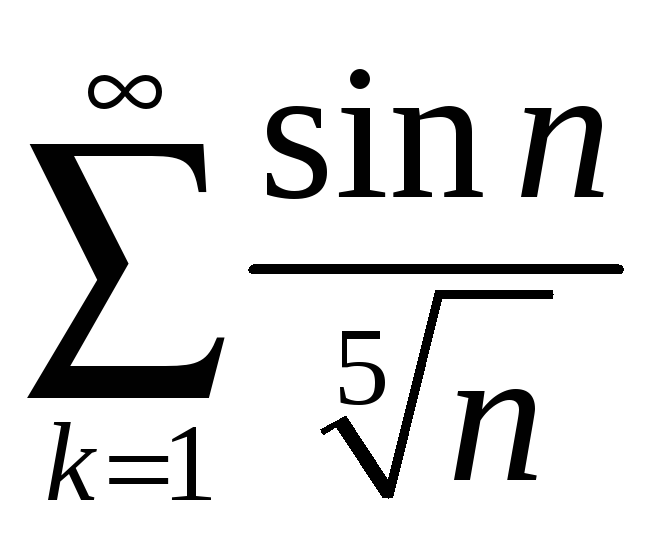 ;
;
2.5
а)
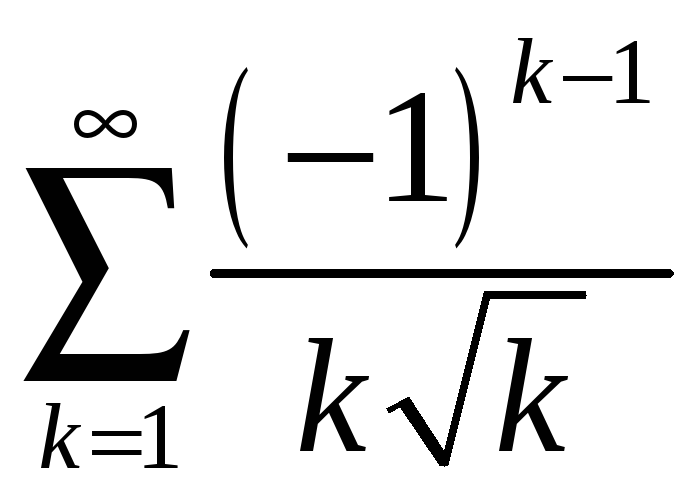 ;
б)
;
б)
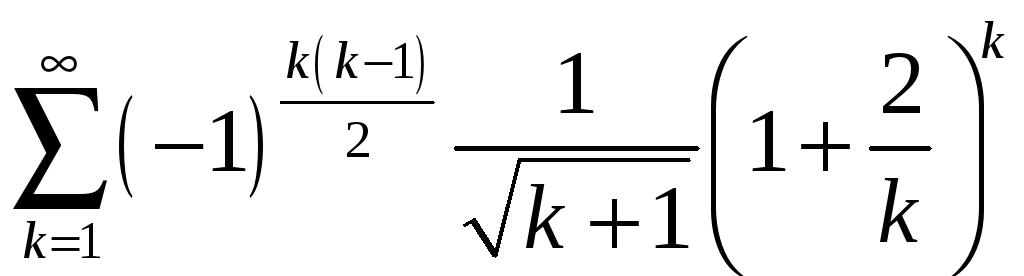 ;
;
2.6
а)
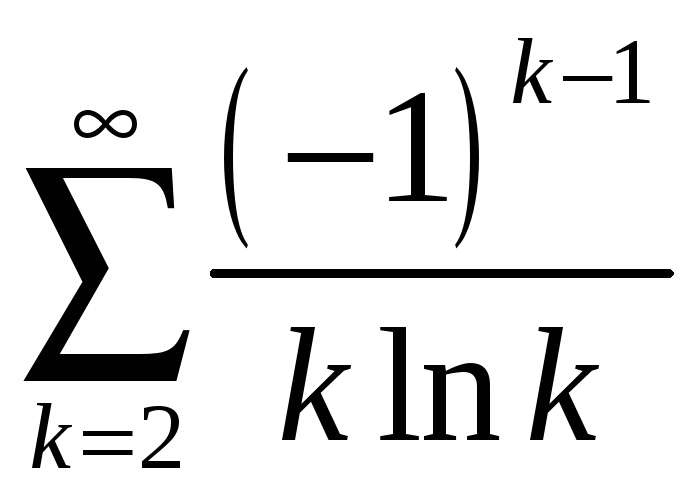 ;
б)
;
б)
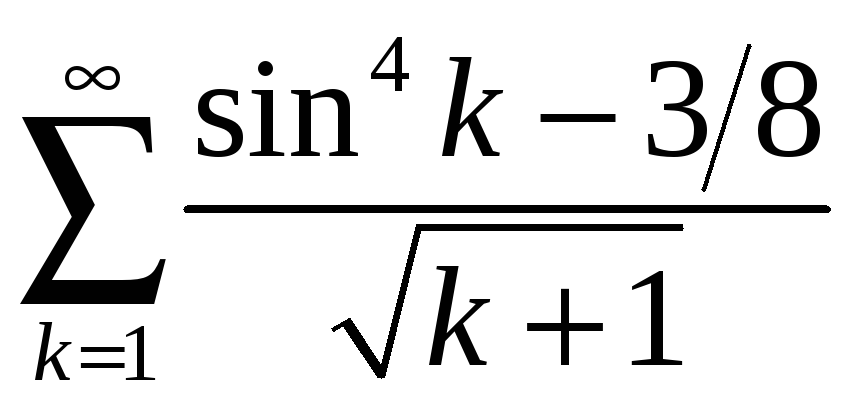 ;
;
2.7
а)
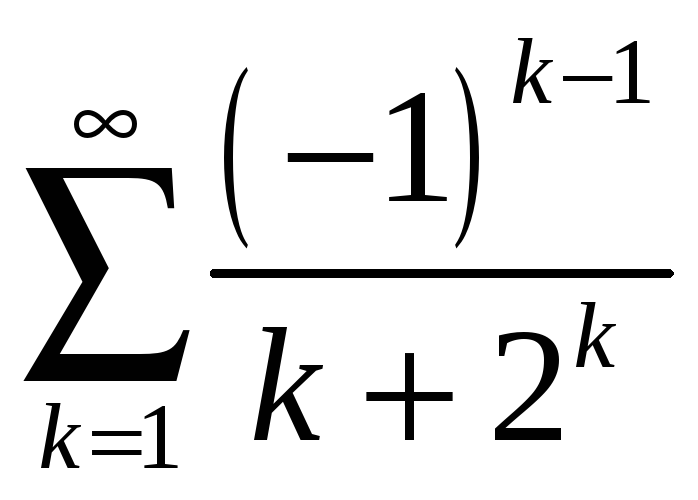 ;
б)
;
б)
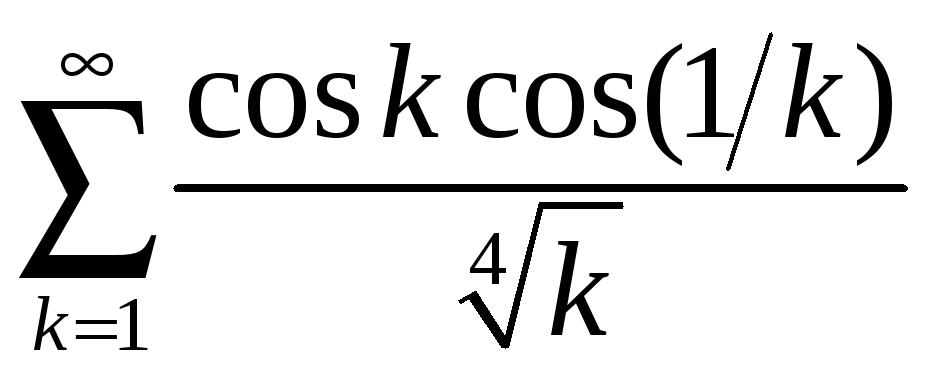 ;
;
2.8
а)
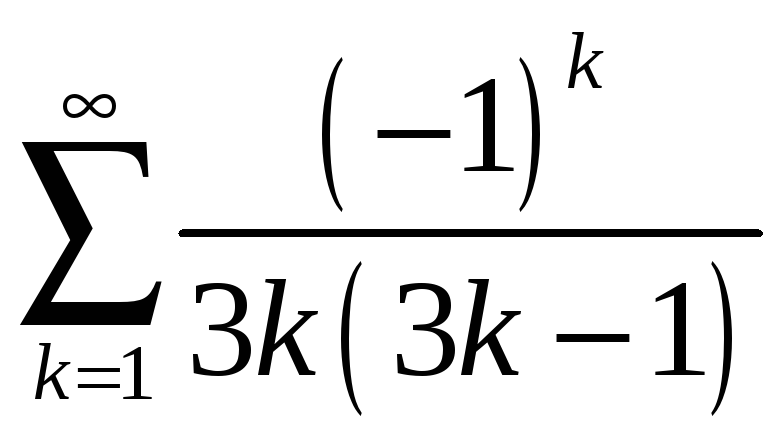 ;
б)
;
б)
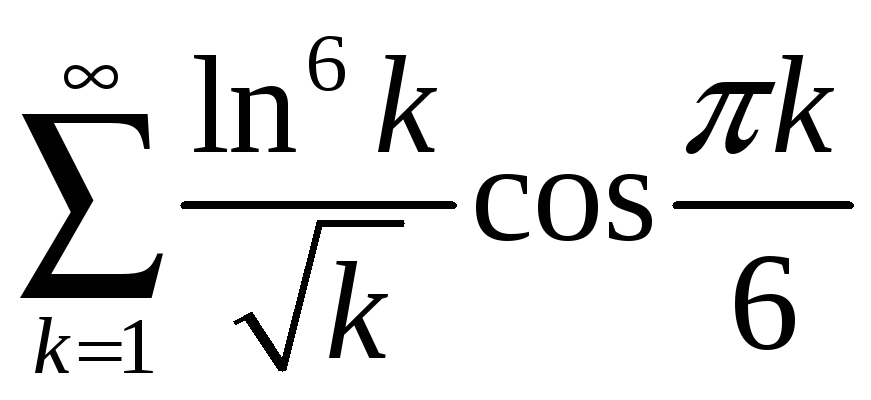 ;
;
2.9
а)
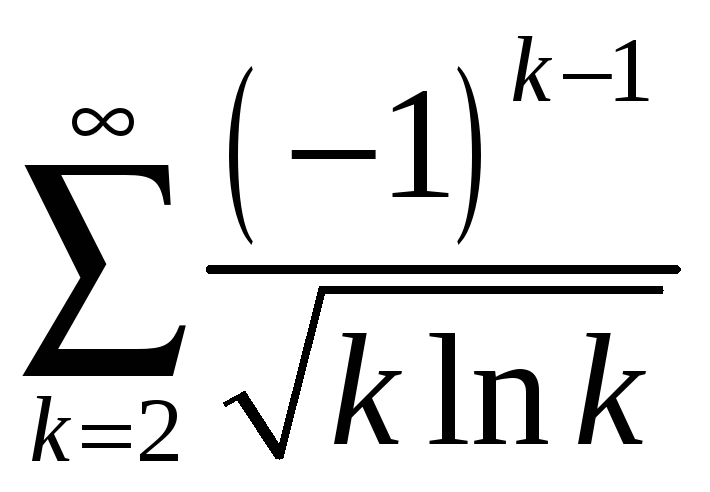 ;
б)
;
б)
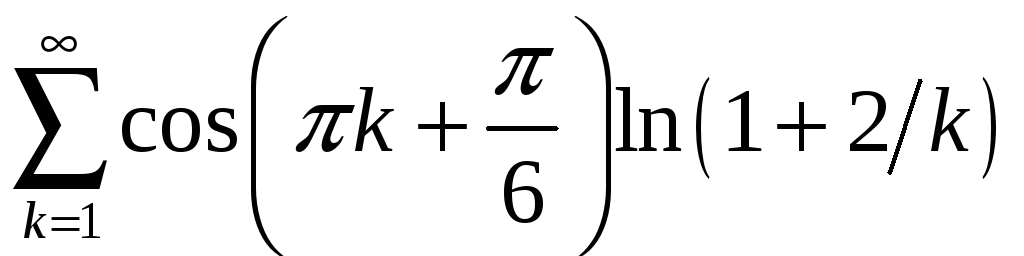 ;
;
2.10
а)
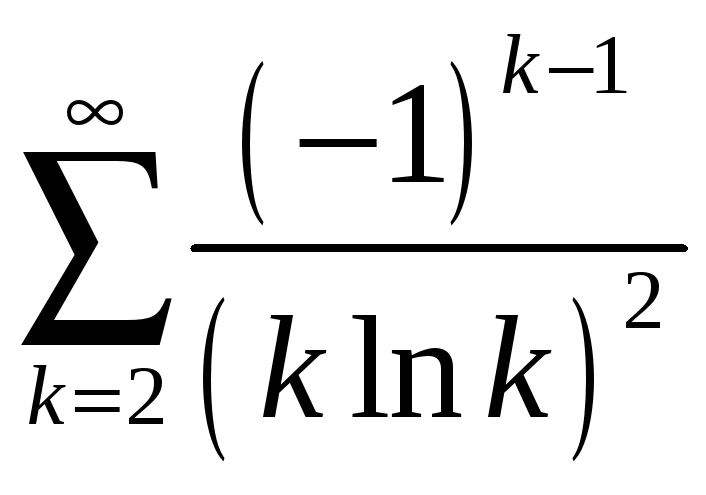 ;
б)
;
б)
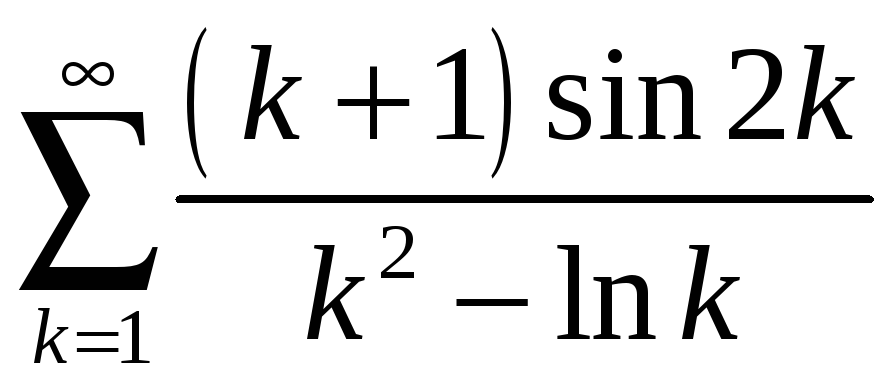 ;
;
2.11
а)
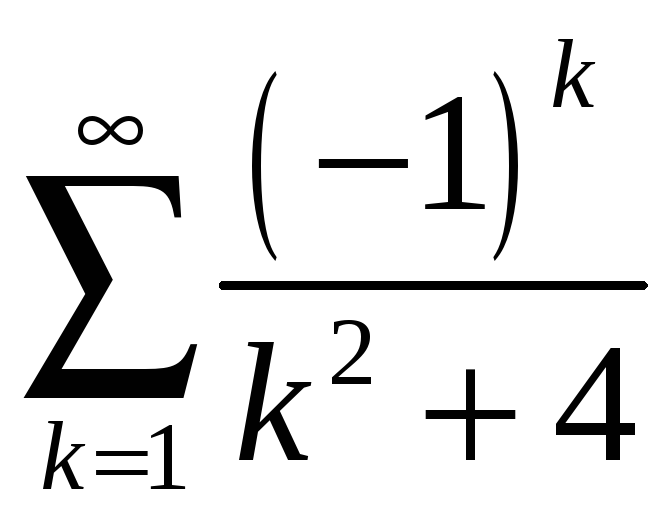 ;
б)
;
б)
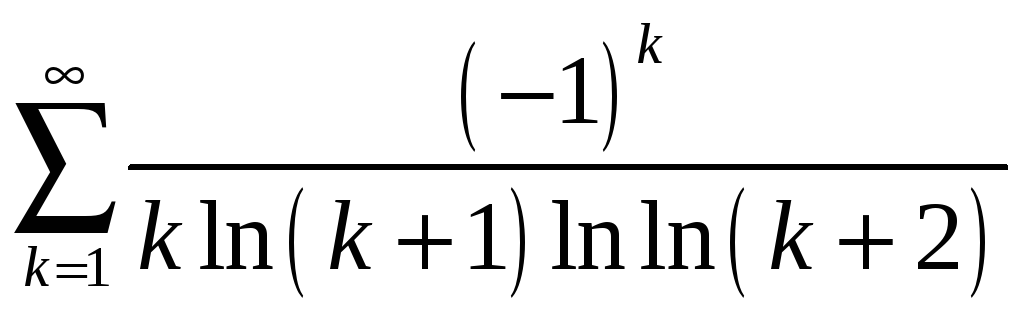 .
.
3.Разные задачи
3.1
Составить сумму рядов
![]() и
и
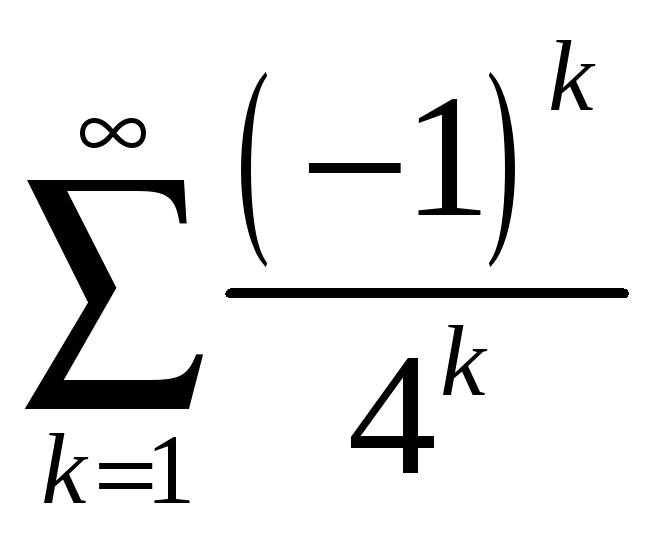 ,
исследовать его сходимость.
,
исследовать его сходимость.
3.2
Составить сумму рядов
![]() и
и
 ,
исследовать его сходимость.
,
исследовать его сходимость.
3.3
Составить сумму рядов
![]() и
и
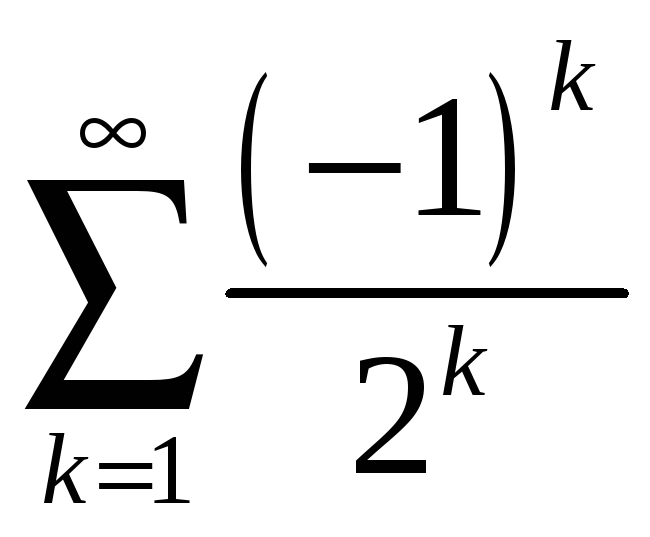 ,
исследовать его сходимость.
,
исследовать его сходимость.
3.4
Составить разность рядов
![]() и
и
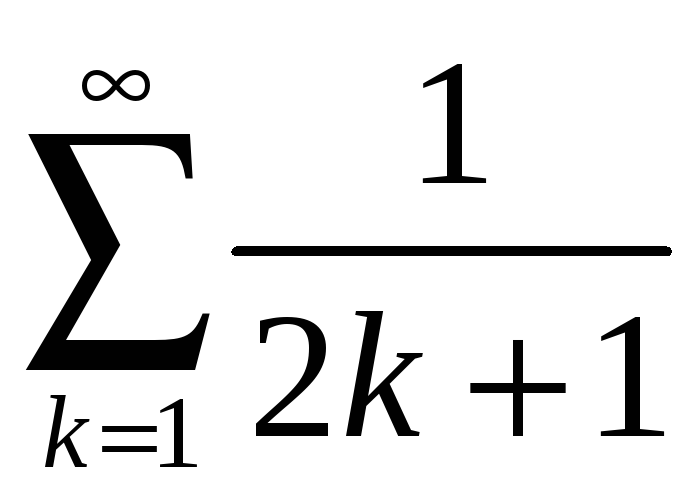 ,
исследовать его сходимость.
,
исследовать его сходимость.
3.5
Сходится ли произведение двух рядов
![]() и
и
![]() ?
?
3.6
Сходится ли ряд, являющийся разностью
рядов
![]() и
и
![]() ?
?
3.7
Сходится ли ряд, являющийся разностью
рядов
![]() и
и
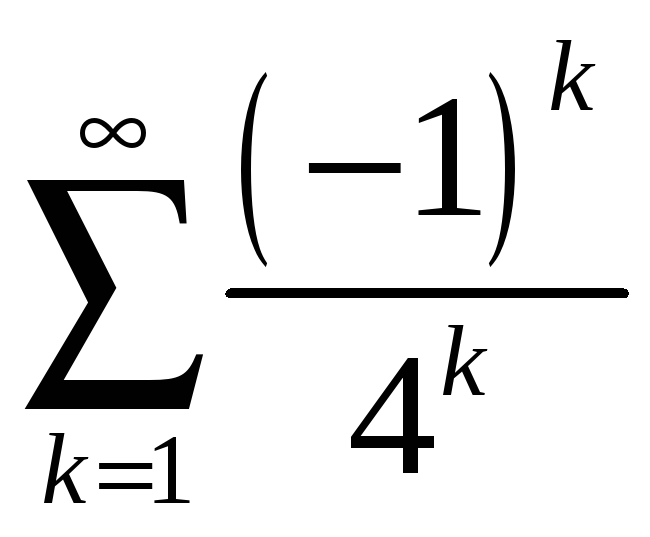 ?
?
3.8
Сходится ли ряд, являющийся разностью
рядов
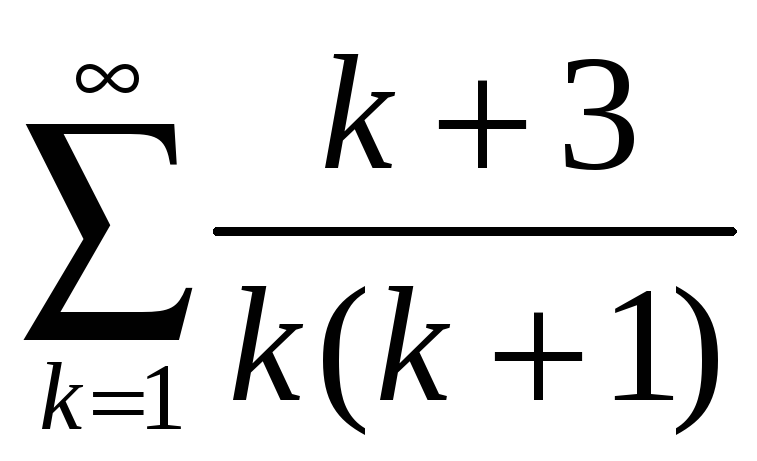 и
и
![]() ?
?
3.9
Показать, что
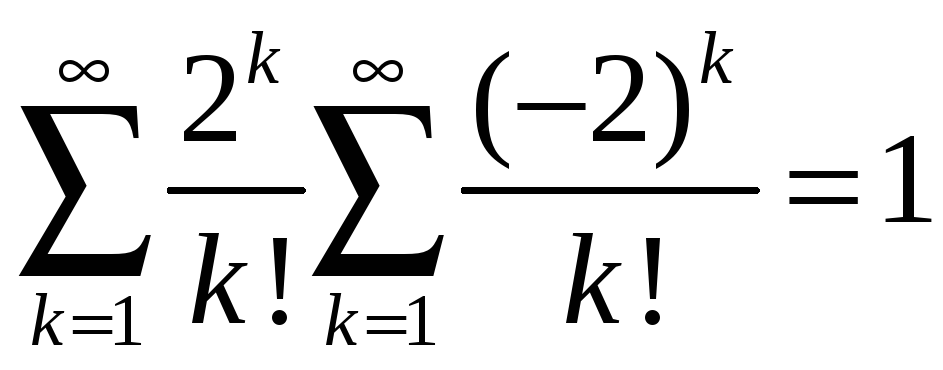 .
.
3.10
Сходится ли произведение рядов:
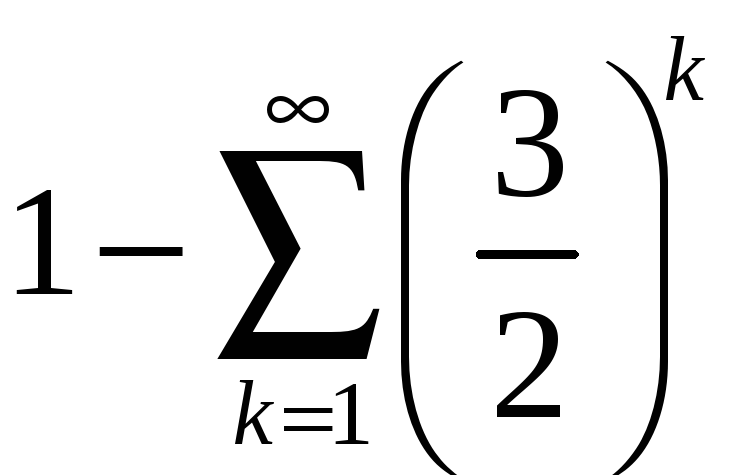 и
и
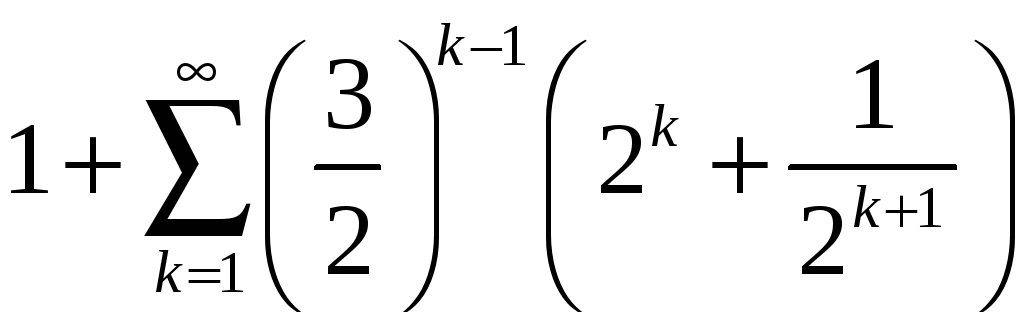 ?
?
4 С точностью до 0,01 вычислить сумму ряда
4.1
![]() ;
;
4.4
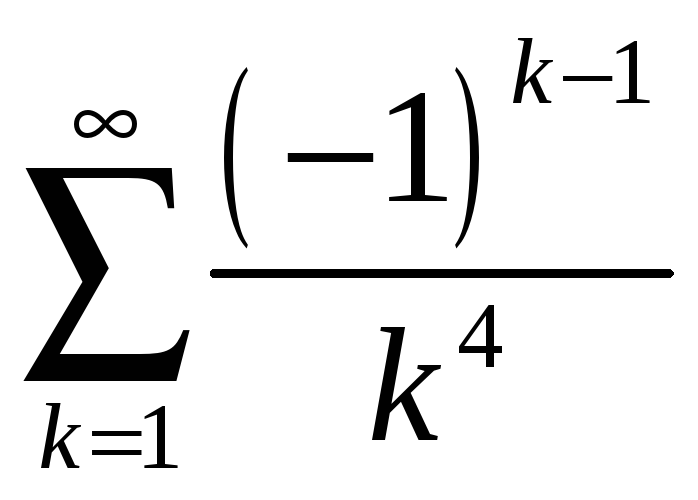 ;
;
4.7
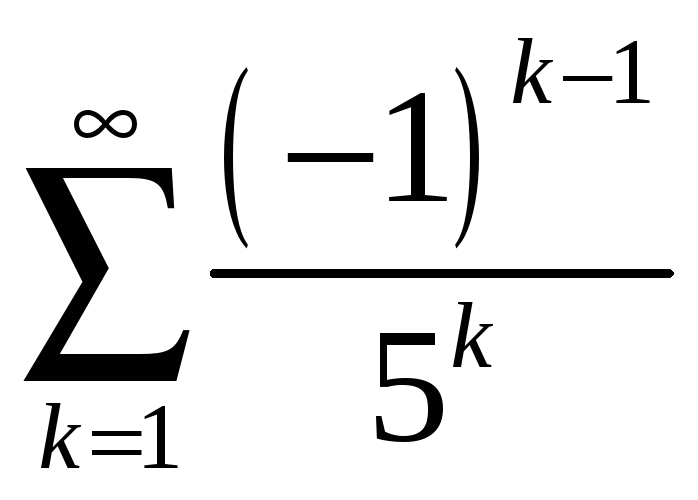 ;
;
4.2
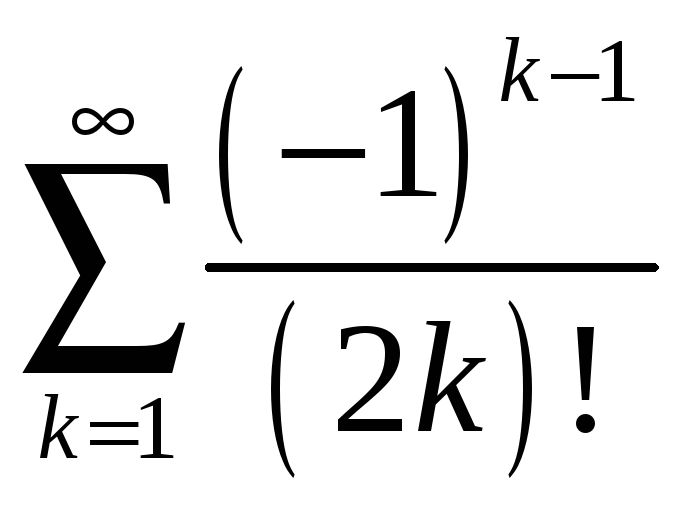 ;
;
4.5
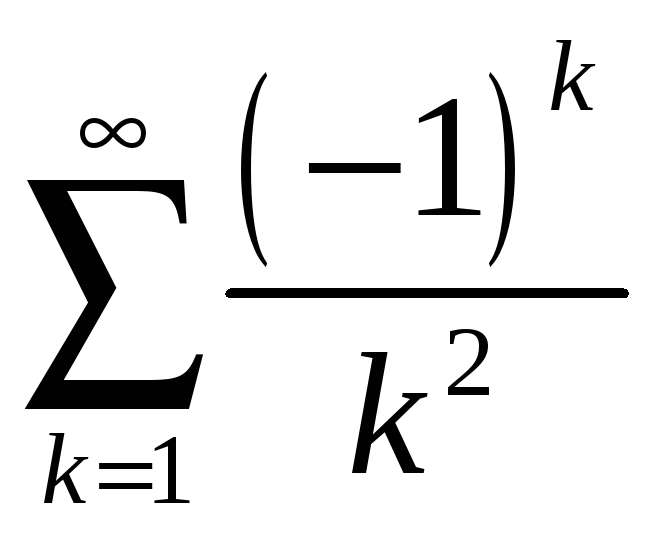 ;
;
4.8
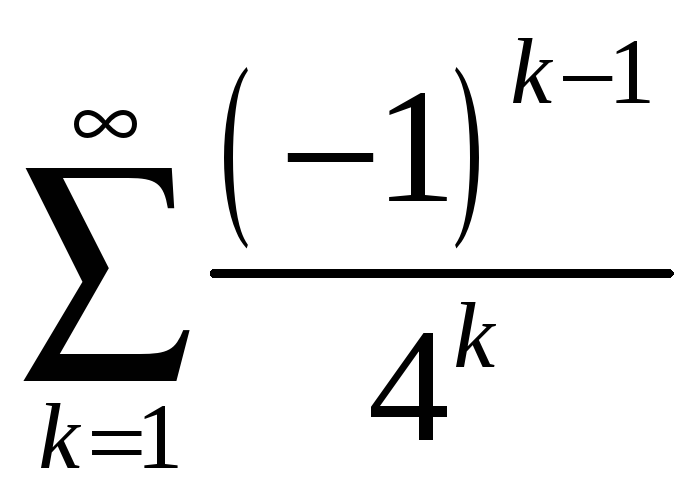 ;
;
4.3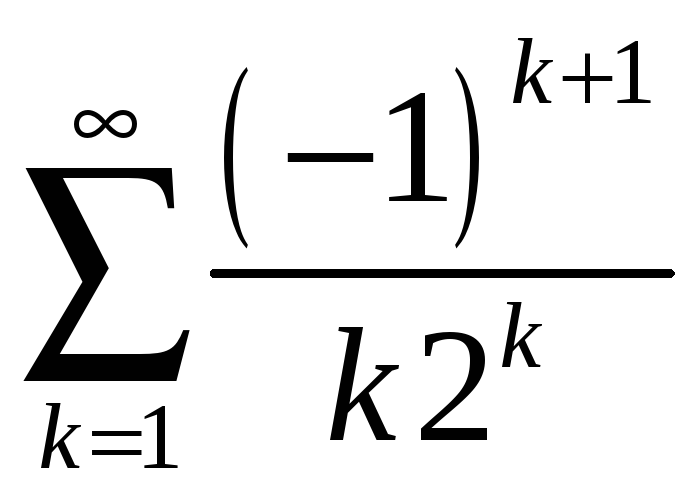 ;
;
4.6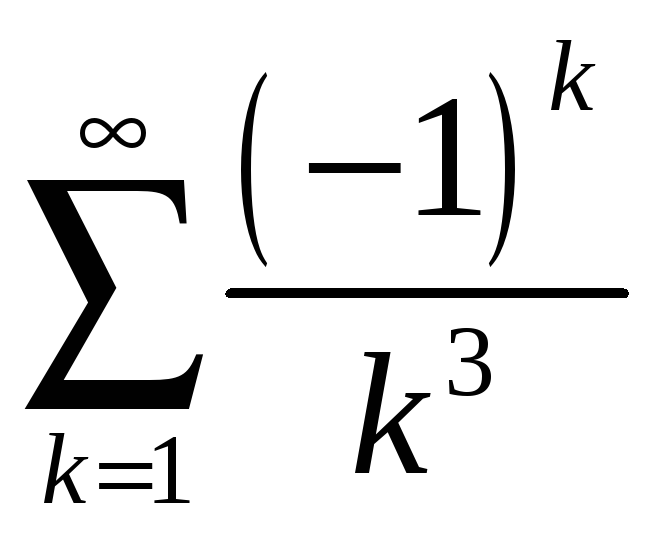 ;
;
4.9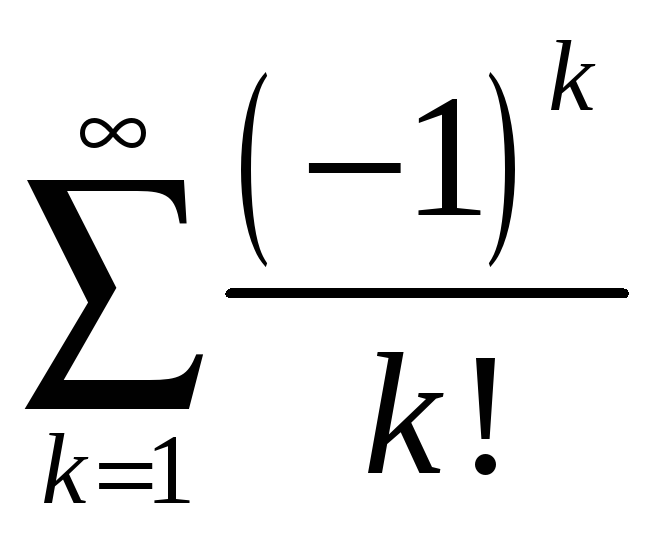 .
.
