Цилиндрические поверхности

Определение. Цилиндрической поверхностью называется множество параллельных прямых (образующих), проходящих через все точки некоторой линии, называемой направляющей.

Пусть цилиндрическая поверхность задана таким образом в прямоугольной системе координат OXYZ, что образующие этой

поверхности параллельны оси OZ, а направляющая лежит в плоскости OXY и задается уравнением:

F(x,у) =0

Если взять произвольную точку M(z,y,z) на цилиндрической поверхности, то ее проекция на плоскость OXY есть точка M₁(х₁,у₁,0). Так как точки M и М₁ лежат на образующей, то х₁=х, у₁=у. А так как точка М₁ лежит на направляющей, то координаты точки М₁, а, значит, и точки M, удовлетворяют уравнению F(x,у)=0.

Итак, уравнению удовлетворяют координаты любой точки

цилиндрической поверхности. Следовательно, уравнение

F(x,у)=0

– искомое уравнение цилиндрической поверхности.

Если в прямоугольной системе координат OXYZ направляющая является кривой второго порядка, задаваемой каноническим уравнением вида F(x,у)=0, а образующие параллельны оси OZ, то цилиндрическими поверхностями второго порядка будут:

1. х²+y²=z² — прямой круговой цилиндр;

2) - эллиптический цилиндр;

3) -гиперболический цилиндр;

4) у²=2рх - параболический цилиндр.

Заметим, что характерной чертой уравнения рассматриваемых цилиндрических поверхностей, является отсутствие в этих уравнениях одной из переменных.

Конические поверхности

Определение. Конической поверхностью называется множество прямых (образующих), проходящих через некоторую точку (вершину) и пересекающих некоторую линию (направляющую).

Коническая ПВП — коническая поверхность с направляющей, являющейся КВП.

Если вершина совпадает с началом прямоугольной системы координат OXY, а направляющей служит эллипс:

То уравнение конической поверхности имеет вид:

– уравнение конической поверхности

Поверхности вращения

Определение. Поверхность называется поверхностью вращения, если она вместе с каждой своей точкой содержит и всю окружность, полученную вращением этой точки вокруг некоторой фиксированной прямой, называемой осью вращении.

Пусть на плоскости YOZ задана кривая линия l уравнением вида

F(y,z)=0

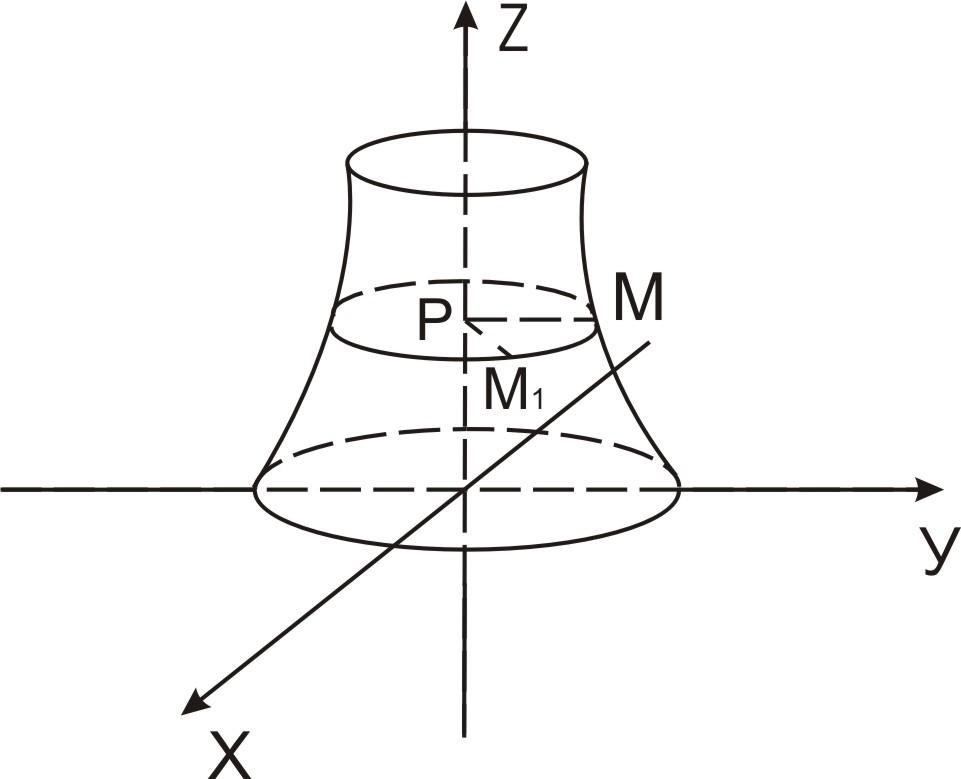
Тогда уравнение поверхности вращения, образованной вращением кривой l вокруг оси OZ имеет вид:

Эллипсоид

Гиперболоид.

Однополостный гиперболоид:

Каноническое уравнение двухполоcного гиперболоида имеет вид:

Параболоид

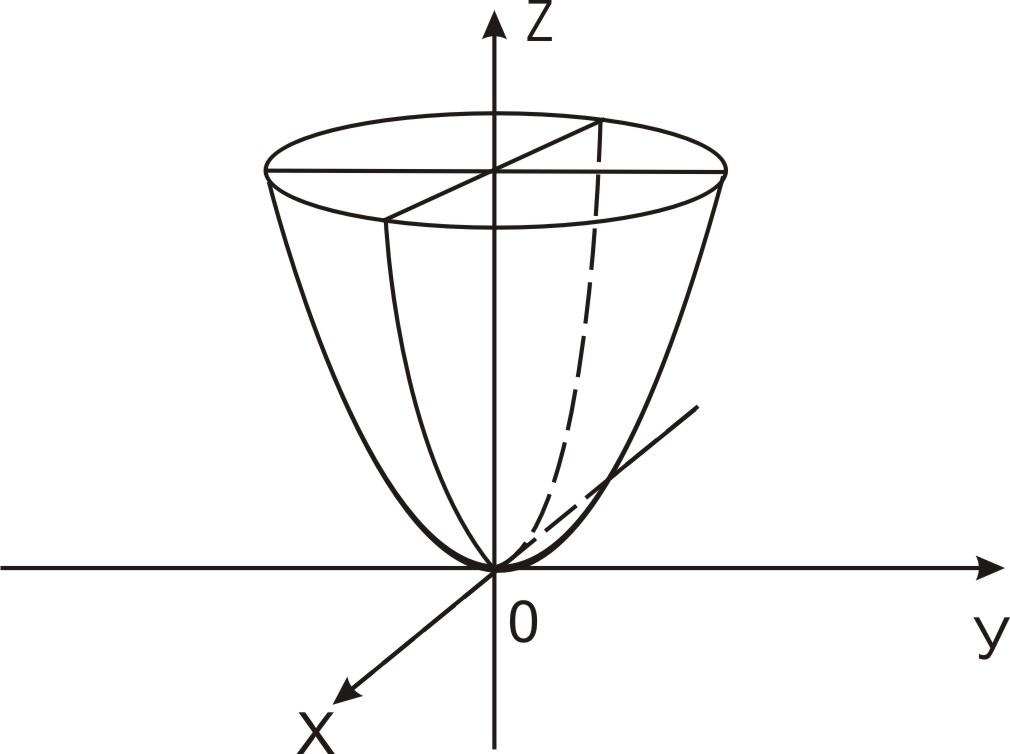
Эллиптический параболоид.

z=ах²+by² (а,b>0).

Гиперболический параболоид.

z=-ax²+by² (a,b>0)

Литература:

1. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М: Наука, 1979.

2. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976.

3. Бузланов А.В., Монахов В.С. Лабораторные работы по курсу «Алгебра и теория чисел». – Гомель: Ротапринт ГГУ им. Ф. Скорины, 1991.

4. Бузланов А.В., Каморников С.Ф., Кармазин А.П. Лабораторные работы по курсу «Алгебра и теория чисел» (раздел «Линейная алгебра») для студентов математического факультета. Часть I, II, III. – Гомель: Ротапринт ГГУ им. Ф. Скорины, 1990, 1991.

5. Бурдун А.А., Мурашко Е.А., Толкачёв М.М., Феденко А.О. Сборник задач по алгебре и аналитической геометрии. – Мн.: Университетское, 1989.

6. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1982.

7. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974.

8. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1968.

9. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. Часть I, II. – Мн.: Вышэйшая школа, 1984, 1987.

10. Рублёв А.Н. Курс линейной алгебры и аналитической геометрии. – М.: Вышэйшая школа, 1972.

Учебное издание

ХОДАЛЕВИЧ АЛЕКСАНДР ДМИТРИЕВИЧ

БОРОДИЧ РУСЛАН ВИКТОРОВИЧ

РЫЖИК ВАЛЕНТИНА НИКОЛАЕВНА