Инварианты кривой второго порядка

Инвариантом уравнения (1) относительно преобразования системы координат ОХУ называется такая функция

f(а₁₁, а₁₂, a₂₂, a₁₃, а₂₃, а₃₃),

которая не меняется при переходе к новой системе координат 0'Х'У'. Таким образом, если f — инвариант, то f(a₁₁,...а₃₃) = f(a'₁₁...а'₃₃).

Теорема. Величины

(6)

являются инвариантами уравнения (1) линии второго порядка

относительно преобразований декартовой системы координат.

Доказательство проведем вначале для преобразования параллельного переноса, а затем для преобразования поворота.

Инвариантность I₁ и I₂ следует из формул (2). Заметим, что из этих формул также следует, что

(7)

Тогда в новой системе координат O’X’Y’

Вычтем из 3-ей строки 1-ю, умноженную на x_0, и затем вторую,

умноженную на у₀. Тогда

Теперь из 3-ro столбца вычтем 1-й, умноженный на x₀ и второй, умноженный на y₀. Получим, что I'₃=I₃.

Рассмотрим теперь преобразование поворота

Разложим I'₃ по элементам 3-го столбца. Получим:

=

(8)

Распишем каждое из 3-х слагаемых в выражении (1.34), пользуясь формулами (1.31).

(9)

(10)

(11)

Следовательно, из (8) следует, что

(12)

Величины А, В, С, углы α, β и I₂ не зависят от угла φ. Значит, при любом повороте системы координат, выражение в правой части (12) не изменяется. С другой стороны, при φ=О, I'₃=I₃. Это и доказывает инвариантность I₃. Теорема доказана.

Определим теперь тип линии в зависимости от знаков инвариантов I₁, I₂ и I₃.

Будем говорить, что

при I₂>О, уравнение (1) задает линию эллиптического типа;

при I₂<О, уравнение (1) задает линии гиперболического типа;

при I₂=О, уравнение (1) задает линии параболического типа.

При параллельном переносе можно попытаться добиться того,

чтобы в уравнении (3) отсутствовали члены 2а'₁₃х' и 2а'₂₃y'. Из формул (2) следует, что это возможно только в том случае, если система

(13)

имеет решение.

Уравнения (13) называются уравнениями центра линии второго порядка. Если х₀, у₀ — решение (13), то точка 0'(х₀,у₀) — центр линии. Если линия имеет центр, то в результате параллельного переноса начала системы координат в точку 0'(х₀,у₀) уравнение линии примет вид

(14)

Поэтому, если точка М(х',у') удовлетворяет уравнению (14), то и точка М'(—х',—у') также удовлетворяет уравнению (14). Таким образом, центр линии является ее центром симметрии.

Заметим, что если кривая второго порядка имеет центр, то, в силу инвариантности I₃, получаем

.

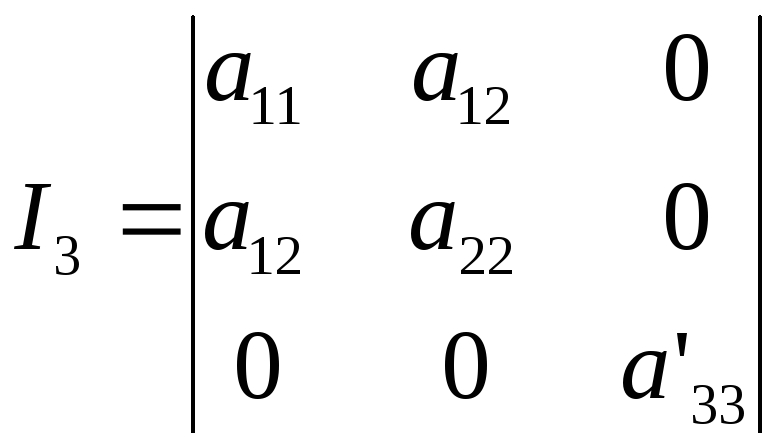Значит,

(15)

Как было показано ранее, можно повернуть систему координат ОXY таким образом, чтобы уравнение (3) не содержало

члена 2а'₁₂х'у'. Ясно, что в этом случае а'₁₂=0 и из формул (4) следует, что

Следовательно, при а₁₂0

(16)

Именно при таком выборе угла поворота, уравнение (3) принимает вид:

(17)

Вывод: путем параллельного переноса приводим уравнение кривой к виду (14)

путем поворота, если а₁₂О, приводим уравнение (14) к виду:

(17)

в системе координат О"Х"У".

Линии эллиптического и гиперболического типов

Если I₂>О, то уравнение (17), согласно (15), можно записать так:

(18)

Так как

то а₁₁а₂₂>О, т.е. коэффициенты а₁₁ и а₂₂ оба отличны от нуля и имеют одинаковые знаки, совпадающие со знаком I₁=a₁₁+а₂₂. Будем в дальнейшем считать, что I₁>О, т.е. а₁₁>0 и а₂₂>0 (если это не так, то умножим обе части (18) на — 1). Заметим, что при такой операции (нормировании) знак I₂ не меняется.

Теорема. Пусть уравнение (1) КВП — эллиптического типа (I₂>О) нормировано так, что I₁>О. Тогда при I₃<0 — это уравнение эллипса. При I₃=0 — единственная точка (уравнение вырожденного эллипса). При I₃>0 — пустое множество точек (уравнение мнимого эллипса).

Доказательство. Так для уравнения (18), I₁=а"₁₁+а"₂₂,

I₂=а"₁₁а₂₂, то из условия I₁>О, I₂>0 следует, что а"₁₁>О, а"₂₂>0. Поэтому уравнение (18) можно записать так:

, при I₃<0; (19)

, при I₃=0; (20)

, при I₃>0; (21)

Теорема доказана.

Теорема. Пусть уравнение (1) - КВП гиперболического типа (I₂<0). Тогда при I₃0 — это уравнение гиперболы, а при I₃=0 - пара пересекающихся прямых.

Доказательство. Так как для уравнения (18):

то из I₂<0 следует а"₁₁, и а"₂₂ имеют разные знаки. Пусть а"₁₁>0, а"₂₂<О, тогда уравнение (18) можно записать так:

, при I₃<0; (22)

, при I₃=0; (23)

, при I₃>0; (24)

Уравнение (22) задает гиперболу, симметричную относительно

оси О"Y".

Уравнение (23) можно переписать так:

– пара пересекающихся прямых в системе координат 0"Х"Y".

Уравнение (24) — каноническое уравнение гиперболы.

Случай, когда а₁₁"<О, а₂₂">0 рассматривается аналогично.

Теорема доказана.